01背包
1.确定dp数组以及下标的含义
dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有两个方向推出来dp[i][j]
2.确定递推公式
- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值,所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
3.初始化
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
如果背包容量j为0的话,即dp[i][0],无论是选取哪些物品,背包价值总和一定为0。
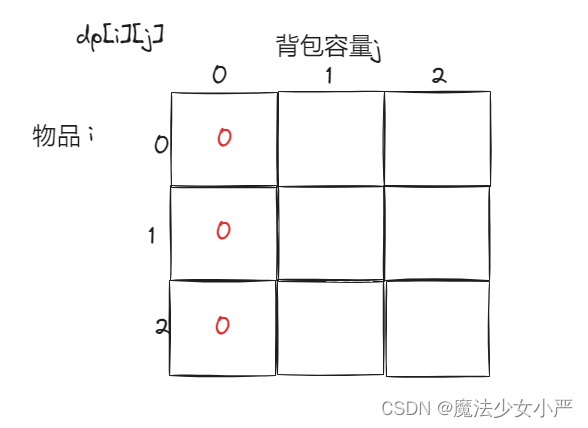
dp[0][j],即:i为0,存放编号0的物品的时候,各个容量的背包所能存放的最大价值。
那么很明显当 j < weight[0]的时候,dp[0][j] 应该是 0,因为背包容量比编号0的物品重量还小。
当j >= weight[0]时,dp[0][j] 应该是value[0],因为背包容量放足够放编号0物品。
4.确定遍历顺序
由递推公式dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);dp[i][j] 是由左上方数值推导出来
先遍历 物品还是先遍历背包重量呢?
其实都可以!!
46. 携带研究材料
时间限制:5.000S 空间限制:128MB
题目描述
小明是一位科学家,他需要参加一场重要的国际科学大会,以展示自己的最新研究成果。他需要带一些研究材料,但是他的行李箱空间有限。这些研究材料包括实验设备、文献资料和实验样本等等,它们各自占据不同的空间,并且具有不同的价值。
小明的行李空间为 N,问小明应该如何抉择,才能携带最大价值的研究材料,每种研究材料只能选择一次,并且只有选与不选两种选择,不能进行切割。
输入描述
第一行包含两个正整数,第一个整数 M 代表研究材料的种类,第二个正整数 N,代表小明的行李空间。
第二行包含 M 个正整数,代表每种研究材料的所占空间。
第三行包含 M 个正整数,代表每种研究材料的价值。
输出描述
输出一个整数,代表小明能够携带的研究材料的最大价值。
输入示例
6 1
2 2 3 1 5 2
2 3 1 5 4 3输出示例
5提示信息
小明能够携带 6 种研究材料,但是行李空间只有 1,而占用空间为 1 的研究材料价值为 5,所以最终答案输出 5。
数据范围:
1 <= N <= 5000
1 <= M <= 5000
研究材料占用空间和价值都小于等于 1000
代码参考:
import java.util.*;
public class Main{
public static void main(String[] args ){
Scanner scanner=new Scanner(System.in);
int m=scanner.nextInt();
int n=scanner.nextInt();
int[][] t=new int[2][m];
for(int i=0;i<2;i++){
for(int j=0;j<m;j++){
t[i][j]=scanner.nextInt();
}
}
int[][]dp=new int[m][n+1];
//初始化
for(int j=0;j<=n;j++){
if(t[0][0]<=j){
dp[0][j]=t[1][0];
}
}
for(int i=1;i<m;i++){
for(int j=1;j<=n;j++){
if(j<t[0][i]) dp[i][j]=dp[i-1][j];
else dp[i][j]=Math.max(dp[i-1][j],dp[i-1][j-t[0][i]]+t[1][i]);
}
}
System.out.println(dp[m-1][n]);
}
}优化上面代码,把二维的dp[][]数组该为一维
在使用二维数组的时候,递推公式:dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
dp数组的第i层只与第i-1层有关
其实可以发现如果把dp[i - 1]那一层拷贝到dp[i]上,表达式完全可以是:dp[i][j] = max(dp[i][j], dp[i][j - weight[i]] + value[i]);
与其把dp[i - 1]这一层拷贝到dp[i]上,不如只用一个一维数组了
该为一维dp数组后,根据地推公式可得,dp[i]都是由其左边的数得到的,所以遍历顺序应该改为从右往左,这样才能让dp[j]利用到上一层的dp[j]
import java.util.*;
public class Main{
public static void main(String[] args ){
Scanner scanner=new Scanner(System.in);
int m=scanner.nextInt();
int n=scanner.nextInt();
int[][] t=new int[2][m];
for(int i=0;i<2;i++){
for(int j=0;j<m;j++){
t[i][j]=scanner.nextInt();
}
}
int[]dp=new int[n+1];
//初始化
for(int j=0;j<=n;j++){
if(t[0][0]<=j){
dp[j]=t[1][0];
}
}
for(int i=1;i<m;i++)
for(int j=n;j>=0;j--){
if(j>=t[0][i])
dp[j]=Math.max(dp[j],dp[j-t[0][i]]+t[1][i]);
}
System.out.println(dp[n]);
}
}dp数组初始化可以统一为0,物品从0开始 开始遍历
import java.util.*;
public class Main{
public static void main(String[] args ){
Scanner scanner=new Scanner(System.in);
int m=scanner.nextInt();
int n=scanner.nextInt();
int[][] t=new int[2][m];
for(int i=0;i<2;i++){
for(int j=0;j<m;j++){
t[i][j]=scanner.nextInt();
}
}
int[]dp=new int[n+1];
//初始化dp[]都为0
for(int i=0;i<m;i++)
for(int j=n;j>=0;j--){
if(j>=t[0][i])
dp[j]=Math.max(dp[j],dp[j-t[0][i]]+t[1][i]);
}
System.out.println(dp[n]);
}
}
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5] 输出:true 解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5] 输出:false 解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 2001 <= nums[i] <= 100
思路:
用01背包问题解决该题,01背包要求一个物品最多取一次,跟这里的求子集的步骤一致,本题要求集合里能否出现总和为 sum / 2 的子集,即在01背包问题中的求价值为sum/2
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
动规五部曲分析如下:
1.确定dp数组以及下标的含义
dp[i]表示背包容量为i时的最大价值
本题中每一个元素的数值既是重量,也是价值。
所以 当 dp[target] == target 的时候,背包就装满了。
2.确定递推公式
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
3.dp数组如何初始化
如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。
4.确定遍历顺序
如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历!
5.举例推导dp数组
class Solution {
public boolean canPartition(int[] nums) {
int sum=0;
for(int i=0;i<nums.length;i++){
sum+=nums[i];
}
if(sum%2==1) return false;
int[] dp=new int[sum/2+1];
for(int j=0;j<nums.length;j++)
for(int i=sum/2;i>=nums[j];i--){
dp[i]=Math.max(dp[i],dp[i-nums[j]]+nums[j]);
}
if(dp[sum/2]== sum/2)return true;
return false;
}
}