1.简介

(1)线性规划三要素

(2)模型适用赛题

2.典例讲解
(1)问题分析
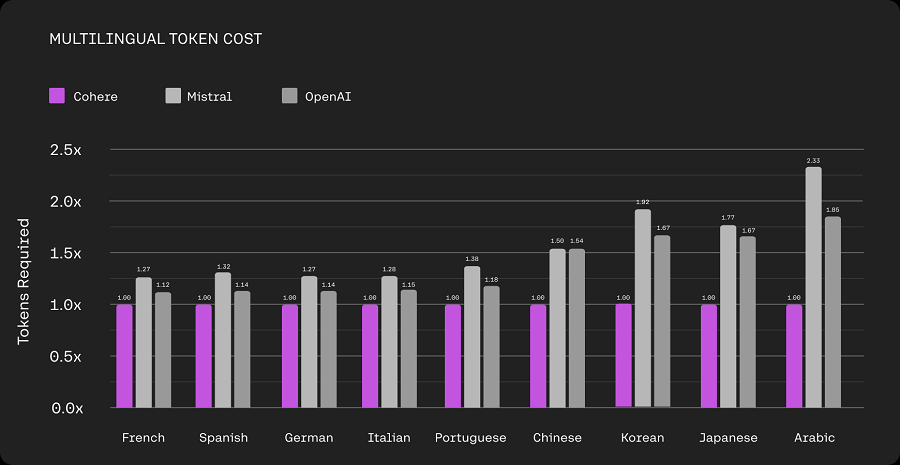
目标函数是净收益尽可能大,风险尽可能小;
约束条件是交易费的分段函数,以及每一笔投资都是非负数;
(2)模型假设
模型假设是我们进行建模的时候必须要进行的,我们应该逐步地学习;对于这道题目,我们首先要理清各个变量的意义,以及不同变量之间的各种关系;这个里面的交易费是一个分段函数,我们的投资小于一个指定的数字的时候,需要付对应的交易费,大于这个数字的时候,只需要按照一定的比率进行付交易费即可,这个指定的数据就是ui,我们举一个很简单的例子,我们的投资以100作为分界线,当我们投资20的时候,我们就要付交易费20,但是如果我们投资是2000(任意大于20的数字,就只需要按照一定的比率付交易费,也就是说不同的投资,我们的交易费的计算方法是不一样的;
我们上面的假设的意义何在呢?假设每一笔交易的投资金额足够大,我们就只需要按照一定的费率付交易费,这样就把原来的分段函数的两种情况变成了只有现在的一种情况,这样就简化了我们的模型,这就是模型假设的意义,相信你已经get到了!
(3)模型建立
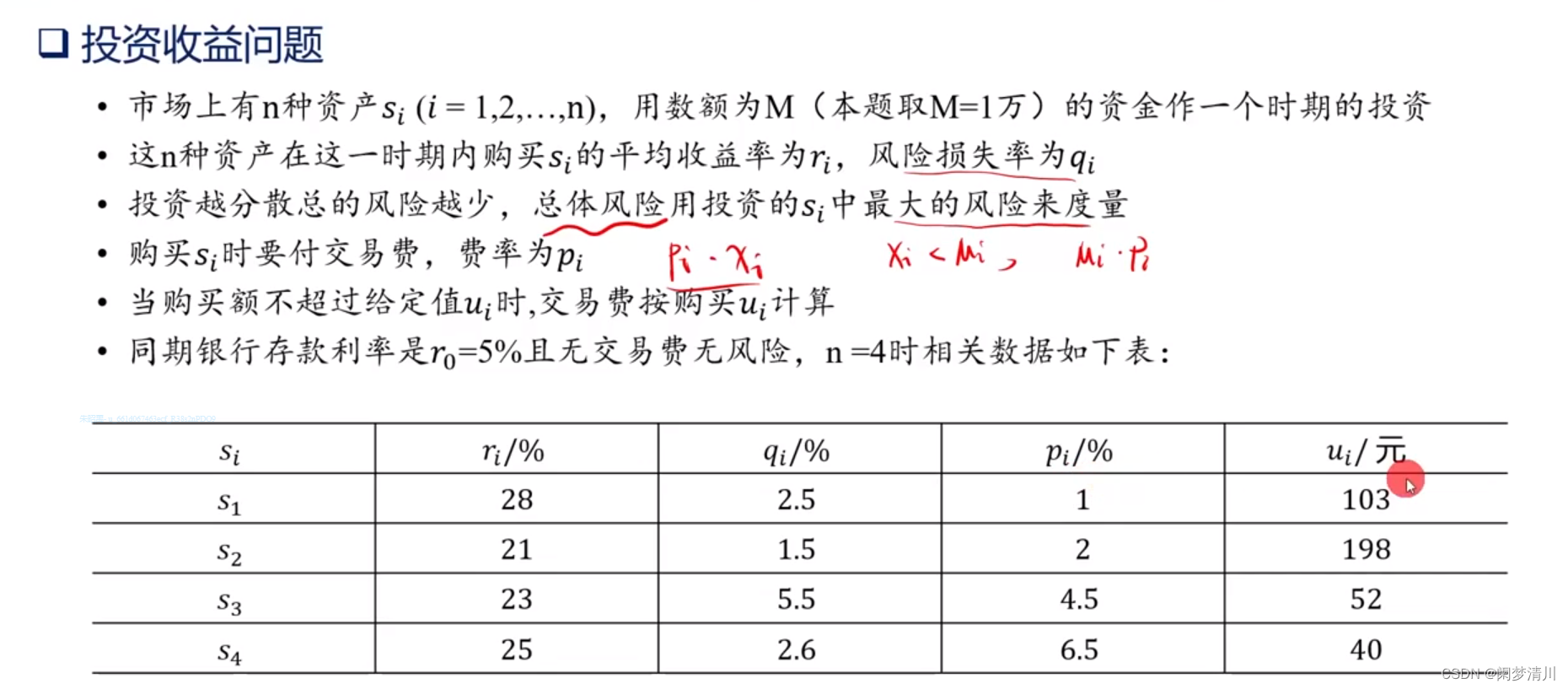
我们上面已经看到了4种投资方案对应的相应的数据,我们下面进行模型的建立;
我们前面已经提到了目标函数和约束条件,下面我们将这些文字语言转换为数学语言;
我们的目标函数就是总利润最大:xi就是每个项目的投资,例如x1就是第一个项目的投资,x1*r1就是投资乘上平均的收益率,得到的就是对应的收益,因为我们还有付的交易费x1*p1就是第一个项目投资的交易费,x1*r1-x1*p1就是我们的第一个项目投资净赚的利润,依次分别计算其他的三个项目的投资,最后求和就是我们的净收益;(但是实际上这里的i是从0开始的,不知道你有没有注意到(我最开始没有注意到),这个就是我们的4个项目的利润收益加上我们的剩下的资金x0,因为x0是不存在交易费的,这个x0是存在银行里面有利息的,所以我们可以直接加上对应的利息,相当于这个收益是前四个项目的收益加上我们这个时候剩下的资金存银行产生的利息);
我们的目标函数还要求总体的风险尽可能小,我们也要分别计算单个项目的投资的风险最后相加,那么单个项目的投资的风险如何计算呢?为什么下面的图片里面又是max又是min,我们应该如何进行理解呢?
这里的max显然是最小值,我们的4种投资都有对应的风险,我们分别计算4种方案的投资风险,在这四个投资风险里面求得最大值(比如我们计算之后发现第3种是风险最大),这个最大值就说明这4个投资里面,3号投资的风险对我们的整个投资的影响最大,我们可以简单地认为只要3好的风险最小,我的这4项投资的风险就最小(这里显然是不够严谨的,但是我们还是忽略了这个误差,有些时候,想要得到精确的解,我们就要付出更大的代价,我们要比较付出的代价是否值得,这里我们认为是没必要的,只要把最大的单个项目的风险降低到最低,我们就近似地认为这4个项目的风险就是最低的),最后我们对这个单个项目的风险求最小值;

约束条件就是我们的投资加上我们的交易费的和等于我们的全部资金,因为我们的资金一部分是投资的,剩下的就是投资的过程中需要付的交易费;xi就是每个项目所投的资金必须是大于0的;
(4)模型简化
合理的模型简化,可以让我们对于模型的求解事半功倍,相信你已经意识到了,前面的分别计算4种投资的风险,取最大值,再求其最小值,让人很不舒服,很对小伙伴难以理解;下面我们对这个目标函数进行简化进而简化我们的模型;
我们假设风险率小于某个确定的值,就是为这个总风险最小,这个确定的值就是a,我们表示出风险率使之小于a,这样简化之后,你就会发现,我们的目标函数,从原来的两个到现在的一个,这个投资风险就变成了一个约束条件,只要求表示的投资风险小于我们的a即可;

经过这个简化之后,我们的模型就是一个目标函数(总的收益最大)和3个约束条件(风险小于这个特定的常数,交易费和我们投入的资金两者的和等于总资金,每一项的投资都是非负数)-----这个就是单目标的线性规划模型;
(也许看到这里,你会觉得,这个模型简化也太神奇了吧,我怎么可能想得到,这个时候,千万不要灰心,我们现阶段只需要理解即可,熟能生巧,数模的学习不能急于求成);
(5)模型改进
我们前面已经提到,不同的人进行投资的时候,所能够承担的风险肯定是不一样的,显示投资里面的a肯定是一个变量,我们在MATLAB调用对应的函数的时候需要这个a是一个常量才可以带入函数,这个时候我们在论文里面写作“模型改进”;
具体的做法就是每次计算的时候,代入的a的值是不一样的,但是我们的模型里面的a是一个常数,我们实际代入的时候把a当作一个变量进行带入;小伙伴们要理解这个思路。
3.模型求解
(1)对MATLAB函数的介绍

理解标准型,把我们的目标函数化为标准型;MATLAB函数使用的时候,我们输入的变量必须是标准型才可以进行求解,标准形是求最小值,我们想要求解的目标函数是净收益的最大值,我们只需要加负号就可以了,具体的操作如下图所示:

(2)函数的参数的介绍
数据来源,计算的时候不要直接拿表格里面的数据运算,后面还是有一个百分号的呦!
下面的就是这个函数进行调用的时候需要使用到的几个对应的参数:
f:计算的就是pi-r1,这里一定要切记后面的百分号,例如,第一个就是银行的p1(交易费0)减去平均收益率(也就是利息0.05)就是图里面的-0.05,第2个是1%-28%即,0.01-0.28=-0.27,依次计算;
A:显然,这个是一个4行5列的矩阵,我们首先要清楚的是这个矩阵的行数和列数分别代表的是什么;A计算的就是对应的风险率;行数4表示的是这4个项目,虽然有5个变量,但是银行存款生利息是没有风险的,所以我们只用这个矩阵的4行分别表示x1,x2,x3,x4;每一行有5个数据,这5个数代表的就是风险损失率,第一个项目的风险就是2.5%,和其他的没有关系,因为我们有5个变量,所以我们写了每行是5个值,如果没有体现这个变量,我们就在对应的位置写上0即可;
b:就是对应的风险,我们模型里面不是把这个风险a设置为常数吗,我们先是让a等于0.05,然后是每次计算换其他的值;所以b这个列向量就是4个0.05;
Aeq:代表的就是第二个约束条件,1加上交易费率,因为银行的没有交易费,所以直接是1,其他的四个都要加上对应的交易费率;
Beq就是我们的M,即总共的资金,我们记作1;
lb:就是每个投资都是非负数,我们的lb就是最小值,即0;最大值其实就是不超过我们的全部资金,即最大值1,但是因为我们前面的约束条件之下,这个单个项目的投资不可能是1,所以这个地方写不写都不会有任何的影响;
(3)MATLAB代码

我们试着理解一下:代码里有一部分就是我们前面分析的过程;
1.clc,clear是清空之前定义的一些变量,防止不必要的报错;
2.zeros(4,1)是生成4行一列的0矩阵,diag是对角矩阵(线性代数知识);
3.LB是5行1列的列向量,全部是0;
4.Q就是净收益,我们还没计算,先定义了一个空的向量,最后把计算的结果放进去即可;
5.循环里面相当于是循环了51次,就是a是以0开始,使用0.001作为步长,以0.5结束,进行求解的,所以是循环了51次,b就是每次循环的时候对应的不同的风险率,4行1列的矩阵;之后调用函数linprog传参求解,MATLAB标准型求的是最小值,我们的循环第四行取相反数得到的是最大值,Q就是最大的投资收益,XX就是对应不同的项目的具体投资金额;
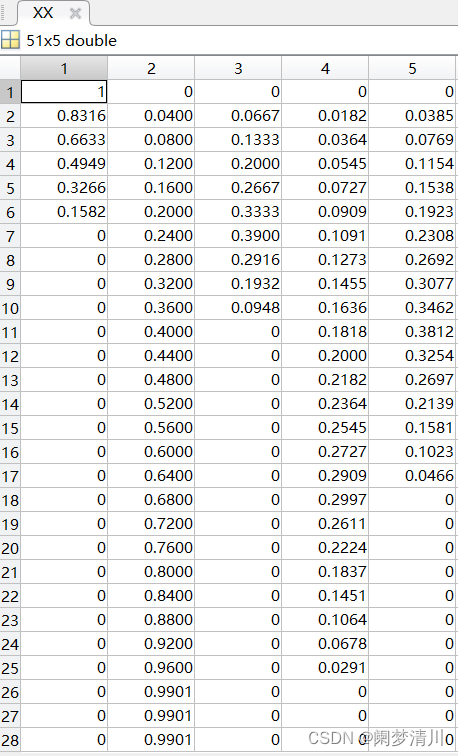
我们通过工作区点击对应的变量就可以查看对应的矩阵,点击xx就可以看到对应每次循环的时候,具体的不同的投资方案;
6.最后的三行就是作图部分的一些命令plot绘制平面坐标轴,*r就是坐标曲线的一种表示的形式,例如是实现还是虚线,使用点还是圆圈,或者是星号,这些等等都有对应的表示方法,读者可以自行的进行了解;
图像:

感兴趣的小伙伴下去可以自行尝试:
clc,clear;
a=[0:0.001:0.05];
f=[-0.05,-0.27,-0.09,-0.185,-0.185];
A=[zeros(4,1),diag([0.025,0.015,0.055,0.026])];
Aeq=[1,1.01,1.02,1.045,1.065];
beq=1;
LB=zeros(5,1);
Q=zeros(1,length(a));
XX=[];
for i=1:length(a);
b=a(i)*ones(4,1);
[x,y]=linprog(f,A,b,Aeq,beq,LB);
Q(i)=-y;
XX=[XX;x'];
end
plot(a,Q,'*r')
xlabel('风险率')
ylabel('最大收益')(4)结果分析
这个计算的结果只是粗略值(不同的软件有偏差),具体的方案:
不同的项目投资金额:可在工作区里面的xx查看;(对应的单位是万元,我们看到的结果要乘上1000才是真正的结果)
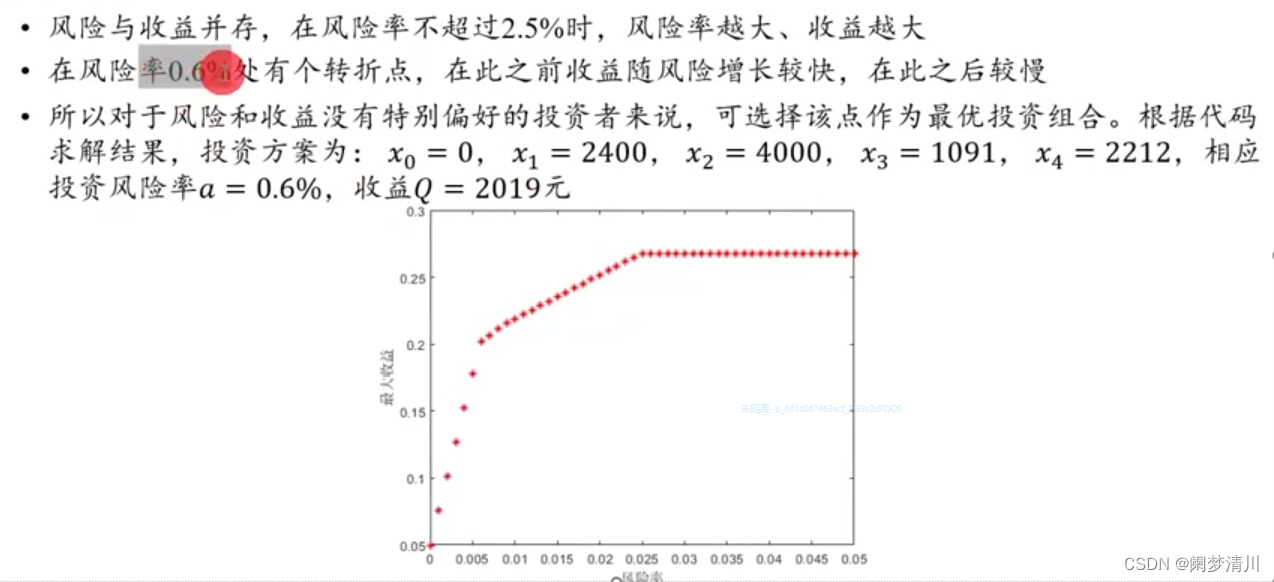
总的净收益Q可在工作区查看;Q是1*51的向量,可以观察到最后的时候收益就已经不变了,和我们的图像结果是吻合的;
能够看到这里,我相信你一定有所收获,上面的文字均是自己的理解,自己的语言,希望能帮助到你,对于任何问题,欢迎在评论区和我交流,感谢!