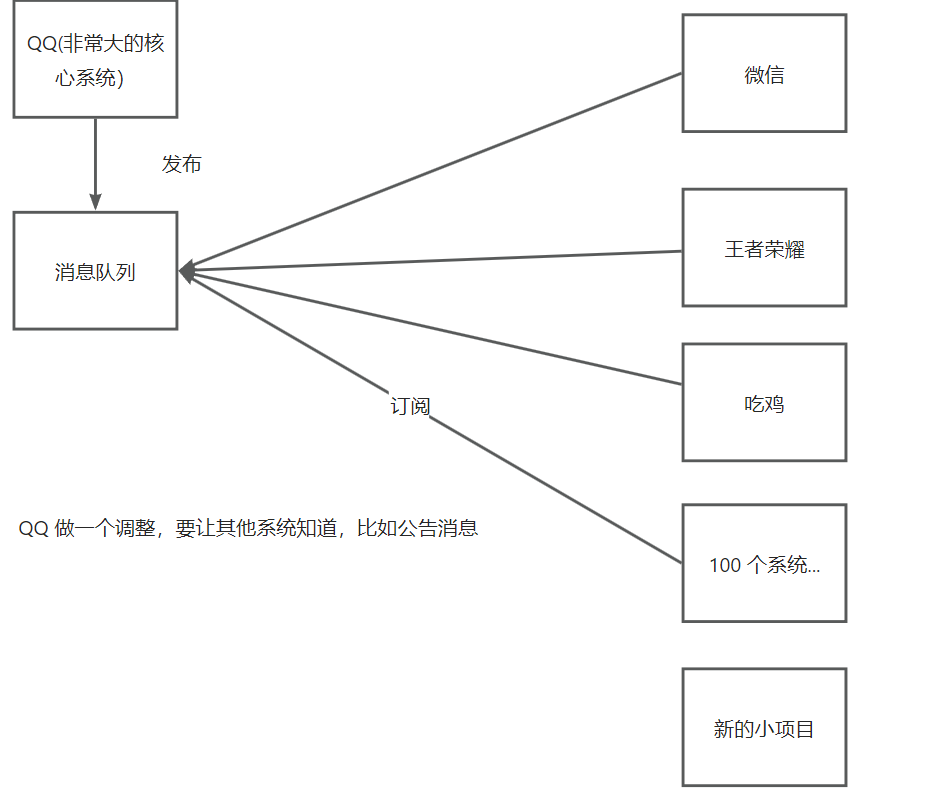
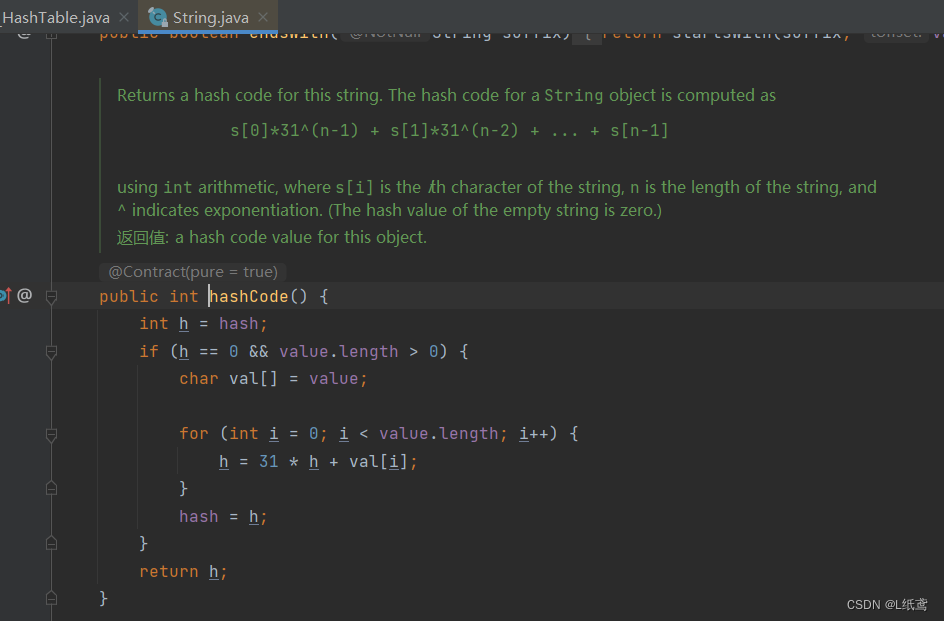
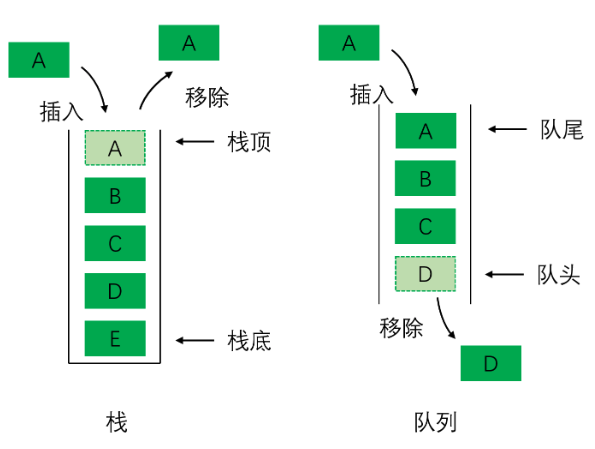
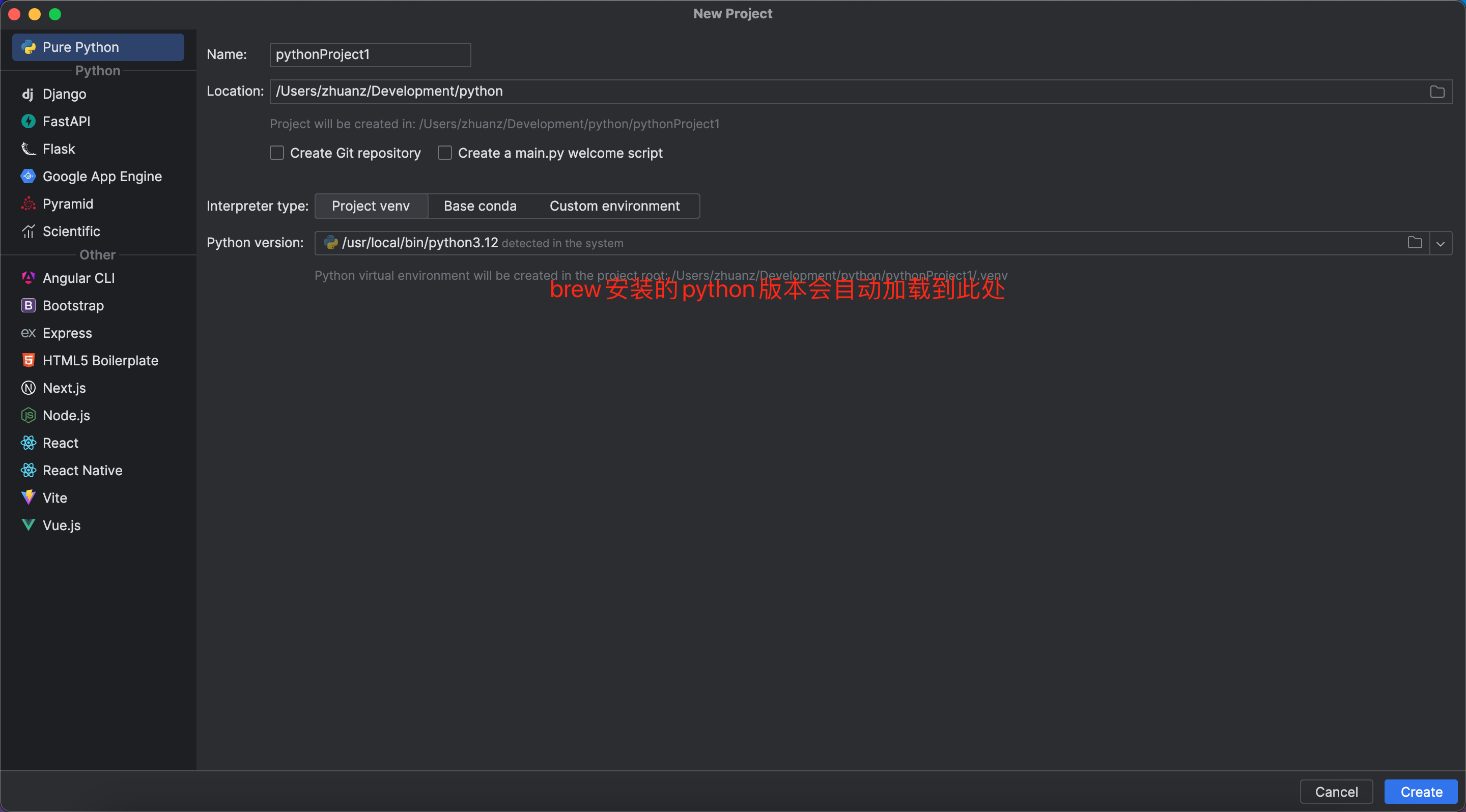
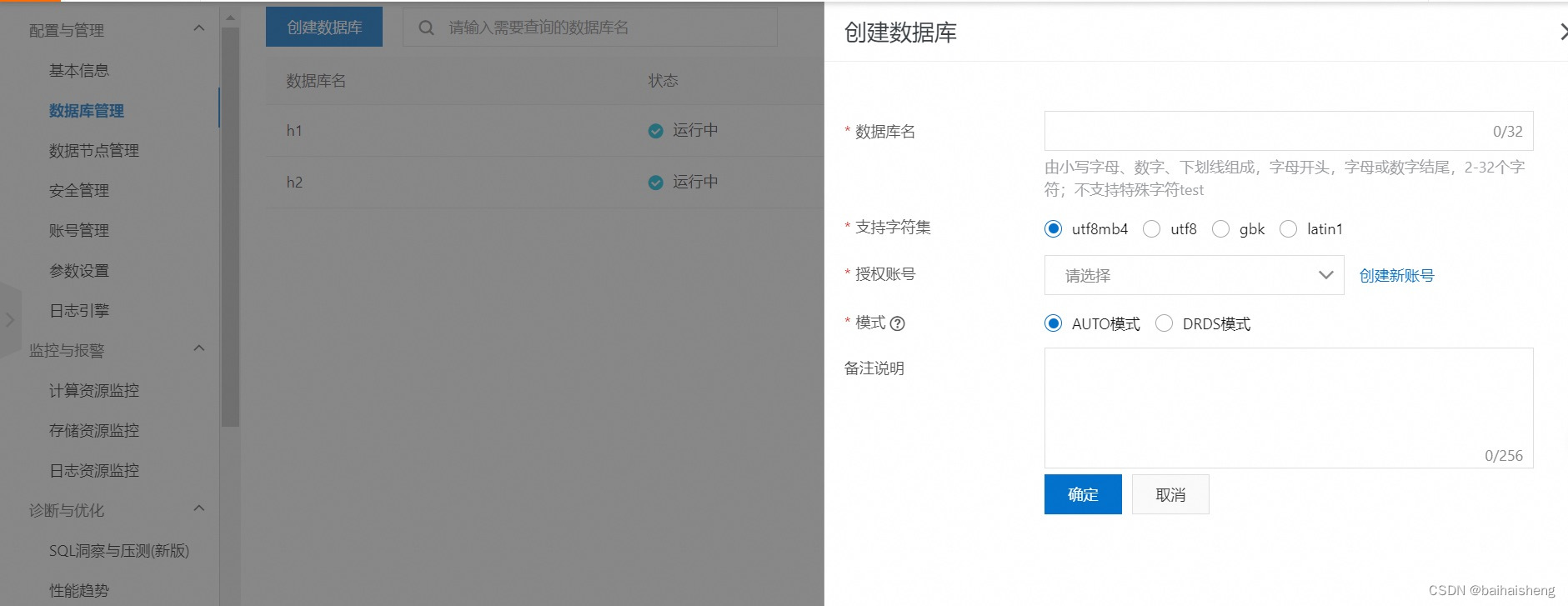
我本来想写在一起的，但是这样的话就没有重点了。分开写更能总结出来问题。这里的步骤5的对称滤波函数确实是(2M-1)x(2N-1)的大小，但是书上还说了如下图所示的问题:

首先第一个问题是乘积的问题，为什么普通的函数乘积也需要填充零？

本来函数相乘添加零是多此一举，但是乘积的结果使用了傅里叶变换或者反变换了，这就有问题。

因为如果不填充零，就不符合卷积定理。为什么一定要符合卷积定理，只有符合了卷积定理，那就可以用公式解释掩模在图像上的滑动的过程了。但是为什么要使用这种方式来修饰图像呢？因为这是修饰图像的基本操作，利用附近的像素修饰中心的像素。所以普通的离散函数乘积使用傅里叶变换或者反变换之前需要填充零。

更具体的说应该是从空间域变到频率域事先要填充零，因为不能在过程中填充，这样就变不回来了。如果变换之后有向量乘法运算，事先也不能不填充零，因为这样反变换之后得到的不是卷积，公式4.7-1看起来没有卷积，但是还是利用了卷积对图像进行了处理，就跟空间域的卷积是一样的过程，不过这里是在中间过程中对频率域进行了修饰。

第二个问题是缠绕误差问题，第一个问题是不填充零导致了缠绕错误，第二个问题是直接取了PXQ的滤波器产生了缠绕误差。这是如何产生的？以一维点列来说明。

假设图像是0 1 2  ，填充之后为0 1 2   0 0，滤波器是a b c b a，如果滤波器不填充零，就是

当x=0的时候，从第0个位置开始，

0 1 2 0 0 0 1 2 0 0 

a a b c b a  a b c b 

如果滤波器填充零，就是

当x=0的时候，从第0个位置开始，

0 1 2 0 0 0 1 2 0 0 

0 a b c b a 0 0 0 0 

如果把填充零的当做是正确的，确实是有差异。那为什么滤波器不填充呢？如果滤波器填充，就是(2P-1)x(2Q-1)点列，而图像是PxQ点列，这样就能使用算法进行乘积再进行傅里叶变换操作了。

首先这个过程的前提是公式4.7-1。原始图像f是MxN点列，填充之后是PxQ点列傅里叶变换为F。当滤波器在频率域中为2Px2Q（写成2Px2Q没有减一是为了方便观察）点列H的时候，需要将图像F也变成2Px2Q才方便乘积和傅里叶变换，这很容易做到，因为只是复制成4份而已。问题就是从PxQ个离散点变成了2Px2Q个离散点，傅里叶反变换之后会得到原来图像的4份复制吗？ 尽管看起来这种复制在函数形式上是一模一样的周期函数，但是采样点不同，就相当于同一个无限采样函数乘以不同长度的简单函数，肯定在傅里叶变换之后不一样了，不会是图像的四份复制。（但是既然能计算得到正确的值，为什么不重新写一个算法增强一下快速傅里叶变换呢？这样图像就不用非要和掩模一个尺寸了，如果这样想，那好不如直接使用空间的卷积公式3.4-2，连傅里叶变换都省略了。）

所以，不能在图像变换之后进行任何改变采样点的操作，因为会改变结果，只能在变换之前操作，但是这样的话，假设直接扩大为2Px2Q，图像在频率域中为F，是充满整个2Px2Q，滤波器大小只能选为2Px2Q，如果选择为PxQ，那么计算还是不准。所以问题又变成了书上的问题了。

所以只能使用滤波器不填充的计算方式，我个人感觉好像是可以完全纠正计算结果的，当然跟滤波器的选择有关。