这里写目录标题
- 快速幂求a^k%p
- 题
- 结
- 快速幂求逆元
- 题
- 结
- 扩展欧几里得求逆元
- 题
- 结
- 排列组合
- 题
- 结
- 二级目录
- 一级目录
- 二级目录
- 二级目录
- 二级目录
- 一级目录
- 二级目录
- 二级目录
- 二级目录
- 一级目录
- 二级目录
- 二级目录
- 二级目录
快速幂求a^k%p
题

结
主要用到a的k次方,可以用多个a的(2的某次)次方的乘积来表示,只需要看次方k的二进制哪些位是1,就相应的乘上该循环步的a
知识点1:要注意如果数的范围很大,那么每两个数相乘,就要将第一个数转为LL,且在最后取模
知识点2:循环条件是k不为0,因为每次处理完之后,k都会去除一位二进制位
快速幂求逆元
题


结
知识点1:适用条件:当模为质数时,才可以使用快速幂求逆元。
知识点2:a在mod p时的逆元,等于 qmi(a, p - 2, p),即a * qmi(a,p - 2, p) = 1 (mod p)
知识点3:要判断是否有解,若a%p!=0,则有解,否则,无解
扩展欧几里得求逆元
题



结
知识点1:与快速幂求逆元相对应,他对模没有要求,所以,当模不是质数时,可以使用扩展欧几里得算法求逆元
知识点2:首先是对gcd算法的展开以及扩展
知识点3:该算法可以求线性同余方程,ax在mod m的情况下,余数是b。可以求出x
他的具体算法过程见“算法一栏”
这里的应用是,将a,m,x,y带入exgcd,得到函数的返回值是gcd(a, m),且x和y会引用返回,其中,x就是我们要找的值的初态,我们还要对其处理。
这里要判断,是否真正要得到的余数b是gcd(a,m)的倍数,如果不是,那么无解,如果是,则结果是x乘上倍数,即x * (b / d),这就是我们要找的x
据此,如果将b换成1,那么就变成了ax在mod m的情况下,余数是1,即x是a在mod m下的逆元
排列组合
题


结
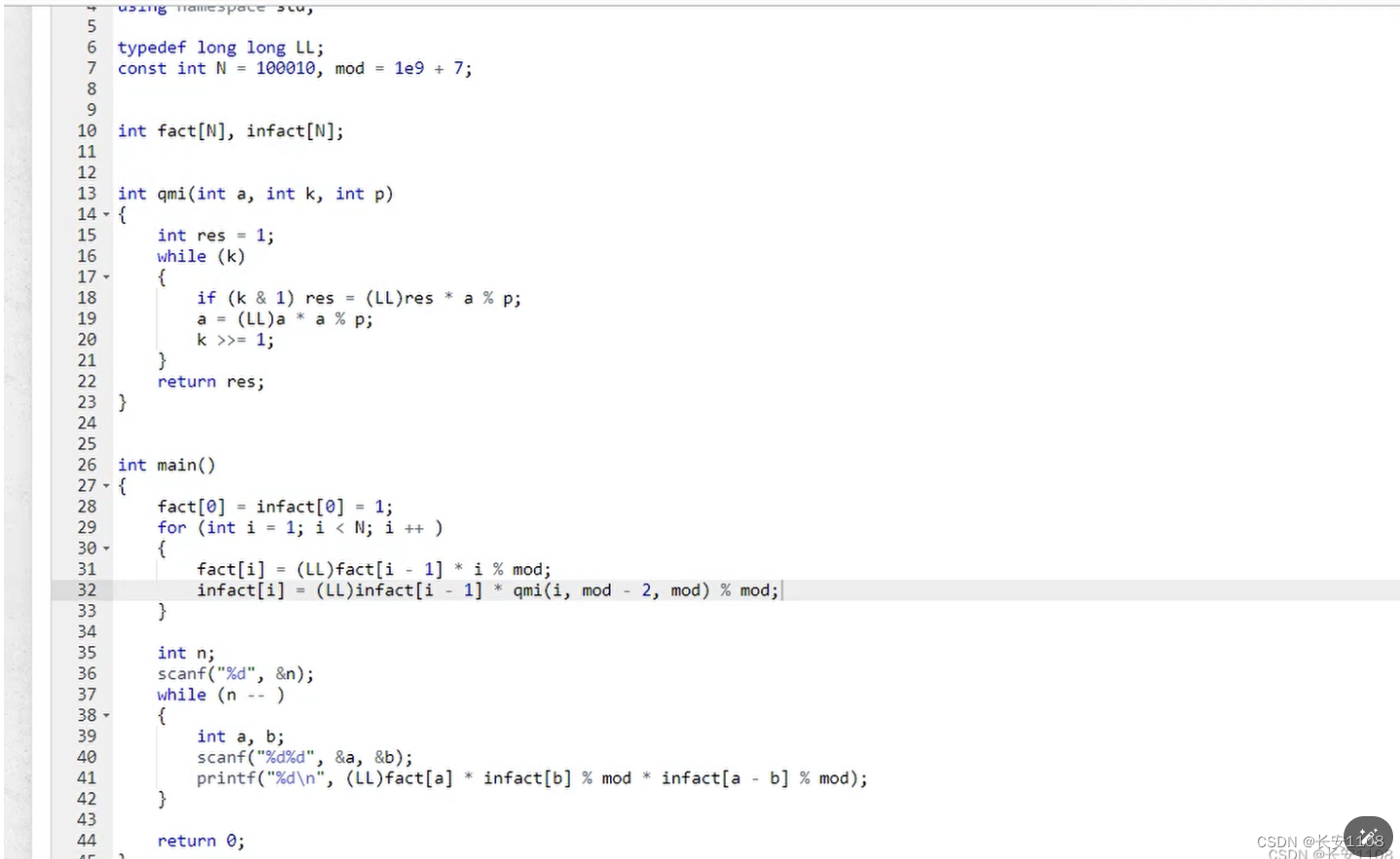
求Cab,使用其阶乘公式,Cab = a!/b!*(a - b)!
知识点1:求阶乘:预处理所有的数的阶乘,以及逆元阶乘,首先初始化fact[0] = infact[0] = 1
之后 i 从1到N,每个fact[i] = fact[i - 1] * i 最后% p
infact[i] = infact[i - 1] * qmi(i, p - 2, p) 最后 % p
然后加个快速幂算法即可
知识点2:从这里我们也可以看出,如果单纯求阶乘,则fact[0] = 1,之后 i 从1到N,每个fact[i] = fact[i - 1] * i