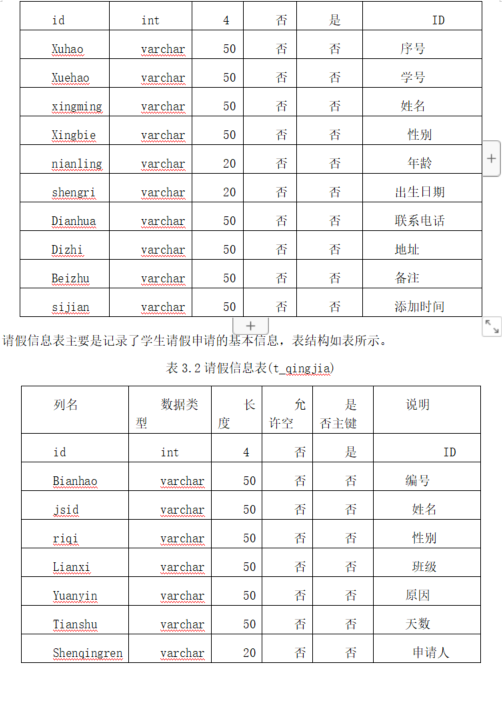
在行和列可自由变换的平面上3点结构有6个

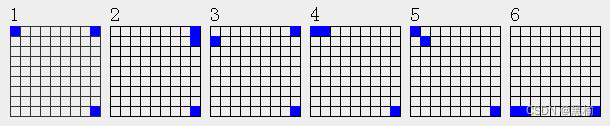
4点结构有16个

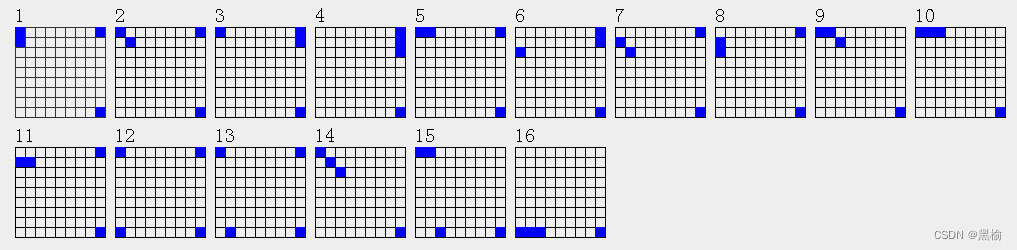
现在计算4a1+3a1，得到结果为

3--5*1--13*4--15*2--19*2--23*2--25*1--35*2--41*2--66*1--69*2--75*2--77*2--85*2--98*1--111*2--118*4--119*6--123*2--190*

有19个7点结构符合要求，其中7a123有6种分解方法可以得到4a1+3a1

计算4a1+3a2

1--1*4--8*1--19*1--28*1--50*6--59*1--85*1--118*

这个结果有8项。

所以方程组

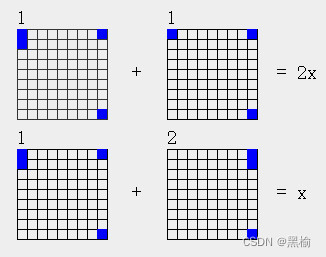
的解x有3项，分别 是7a19，7a85，7a118

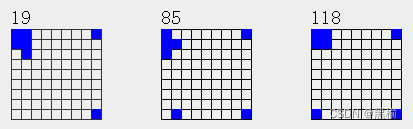
简写为

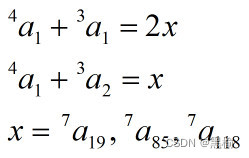
用同样的办法计算4a1+3a3

4--1*6--2*3--3*3--7*3--11*2--12*2--13*6--15*2--19*1--20*1--21*1--23*2--25*4--29*2--30*3--38*4--46*2--50*1--51*2--57*1--69*2--75*2--77*2--80*2--85*2--88*2--98*1--111*2--118*6--123*3--168*1--190*

4a1+3a4=

2--14*2--18*1--22*2--24*1--26*2--27*1--31*1--32*1--33*3--34*1--40*2--49*1--55*1--60*1--62*2--65*4--67*1--73*1--82*1--92*1--93*2--127*2--137*1--165*4--170*1--197*2--199*

4a1+3a5=

4--4*4--6*2--9*2--10*2--14*1--16*1--17*1--26*4--27*1--32*2--34*2--37*2--39*1--43*1--44*1--60*1--62*2--64*2--67*1--121*6--128*2--129*1--130*1--165*2--170*

4a1+3a6=

1--34*1--36*1--40*1--42*1--93*1--105*

把这6项的结果数列合并，得到

5--1*6--2*3--3*4--4*3--5*4--6*3--7*4--8*2--9*2--10*3--11*2--12*3--13*4--14*10--15*1--16*1--17*2--18*5--19*1--20*1--21*1--22*3--23*2--24*4--25*2--26*6--27*1--28*4--29*2--30*1--31*2--32*1--33*6--34*1--35*1--36*2--37*3--38*2--39*2--40*2--41*1--42*1--43*1--44*4--46*2--49*3--50*1--51*1--55*2--57*6--59*2--60*2--62*2--64*2--65*2--66*6--67*2--69*1--73*4--75*4--77*2--80*1--82*5--85*2--88*1--92*2--93*4--98*1--105*2--111*5--118*4--119*1--121*12--123*2--127*6--128*2--129*1--130*2--137*2--165*3--168*6--170*3--190*1--197*2--199*

总的结果数列共有85项，7点结构数列共有211项，用这6个加法可以得到总数量的40%。

其中前44项是连续的，从45项开始变的稀疏

其中的前50项

	1	2	3	4	5	6	7	8	9	10
1					3--5
2	1--1							4--8
3	4--1	6--2	3--3				3--7
4
5				4--4		4--6			2--9	2--10
6
	5--1	6--2	3--3	4--4	3--5	4--6	3--7	4--8	2--9	2--10
	11	12	13	14	15	16	17	18	19	20
1			1--13		4--15				2--19
2									1--19
3	3--11	2--12	2--13		6--15				2--19	1--20
4				2--14				2--18
5				2--14		1--16	1--17
6
	3--11	2--12	3--13	4--14	10--15	1--16	1--17	2--18	5--19	1--20
	21	22	23	24	25	26	27	28	29	30
1			2--23		2--25
2								1--28
3	1--21		1--23		2--25				4--29	2--30
4		1--22		2--24		1--26	2--27
5						1--26	4--27
6
	1--21	1--22	3--23	2--24	4--25	2--26	6--27	1--28	4--29	2--30
	31	32	33	34	35	36	37	38	39	40
1					1--35
2
3								3--38
4	1--31	1--32	1--33	3--34						1--40
5		1--32		2--34			2--37		2--39
6				1--34		1--36				1--40
	1--31	2--32	1--33	6--34	1--35	1--36	2--37	3--38	2--39	2--40
	41	42	43	44	45	46	47	48	49	50
1	2--41
2										1--50
3						4--46				2--50
4									2--49
5			1--43	1--44
6		1--42
	2--41	1--42	1--43	1--44		4--46			2--49	3--50

从结果上看并不是任意结构方程组都有解，比如4a1+3a1和4a1+3a6就没有解。解的数量也不一定一致，比如4a1+3a1和4a1+3a3有7a13,15,19,23,25,69,75,77,85,98,111,118,123,190共14组解。特别是7a19，85，118是4a1+3a1，4a1+3a2，4a1+3a3的共同解。7a34是4a1+3a4，4a1+3a5，4a1+3a6的共同解。最多也只能在3个等式间找到共同解。