【Leetcode】代码随想录Day16

【Leetcode】代码随想录Day16｜二叉树3.0

news2024/9/20 8:00:40

文章目录

- 104 二叉树的最大深度
- 559 n叉树的最大深度
- 111 二叉树的最小深度
- 222 完全二叉树的节点个数

104 二叉树的最大深度

递归法：无论是哪一种顺序，标记最大深度

class Solution(object):
    def depthHelper(self, root, depth):
        if root:
            depth += 1
            left_depth = self.depthHelper(root.left, depth)
            right_depth = self.depthHelper(root.right, depth)
            return max(left_depth, right_depth)
        return depth

    def maxDepth(self, root):
        depth = 0
        if root:
            depth = self.depthHelper(root, depth)
        return depth

优解参考简化：

class Solution(object):
    def maxDepth(self, root):
        if not root:
            return 0
        ldepth = self.maxDepth(root.left)
        rdepth = self.maxDepth(root.right)
        return max(ldepth,rdepth) + 1

迭代法：层序遍历

class Solution:
    def maxDepth(self, root: TreeNode) -> int:
        if not root:
            return 0
        
        depth = 0
        queue = collections.deque([root])
        
        while queue:
            depth += 1
            for _ in range(len(queue)):
                node = queue.popleft()
                if node.left:
                    queue.append(node.left)
                if node.right:
                    queue.append(node.right)
        
        return depth

559 n叉树的最大深度

递归法：需要遍历每个节点的children

"""
# Definition for a Node.
class Node(object):
    def __init__(self, val=None, children=None):
        self.val = val
        self.children = children
"""

class Solution(object):
    def maxDepth(self, root):
        if not root:
            return 0
        childDepth = 0
        if root.children:
            childDepth = max([self.maxDepth(child) for child in root.children])
        return 1 + childDepth

111 二叉树的最小深度

初始思路：
与最大深度一样

class Solution(object):
    def minDepth(self, root):
        if not root:
            return 0
        ldepth = self.minDepth(root.left)
        rdepth = self.minDepth(root.right)
        return min(ldepth,rdepth) + 1

问题：
最大深度只要有一个分支有更深的深度，取这个深度就可以了，所有累积到此的分支都是存在的，他们的深度代表了树的深度。但是上述方法中的最小分支却可能是树并不存在的分支，也就不能代表树的深度。如下面这个例子，这个树的深度是3，但是如果用与之前类似的方法，那么在1这个root左子树不存在的时候，就会认为找到了最短的路径深度1。事实上1并不是叶子结点，并不符合对与树深度的定义。所以在找最小路径的时候，要考虑找到的深度究竟能不能算做是整个树的深度。

转换思路：
需要判断分支深度为0的情况，如果有且只有一个分支深度为0，那么这个后面的深度是需要算上的，并不能因为其中一个分支深度为0，就在这里截止，当作最小深度的情况。

class Solution(object):
    def minDepth(self, root):
        if not root:
            return 0
        
        left = self.minDepth(root.left)
        right = self.minDepth(root.right)
        minDepth = 0
        if left == 0 and right != 0:
            minDepth = right
        elif left != 0 and right == 0:
            minDepth = left
        else:
            return 1 + min(left, right)
        return 1 + minDepth

222 完全二叉树的节点个数

1. 初始思路：
递归或迭代遍历所有节点

递归

class Solution(object):
    def countNodes(self, root):
        if not root:
            return 0
        
        left = self.countNodes(root.left)
        right = self.countNodes(root.right)
        return left + right + 1

Complexity
time: O(n)
space: O(log n)，算上了递归系统栈占用的空间

迭代：

Complexity
time: O(n)
space: O(n)

2. 利用完全二叉树的特性：

首先我们最想用的肯定是满二叉树，因为直接通过层数就可以算出来节点数量2^h - 1。但是完全二叉树可能有两种情况：

满二叉树
距离满二叉树只有最后一层按顺序没有填满

为了能够利用简介的满二叉树算法，我们可以通过递归去将输入的树拆解成子满二叉树。对于一个完全二叉树来讲，会有两种拆解方式：
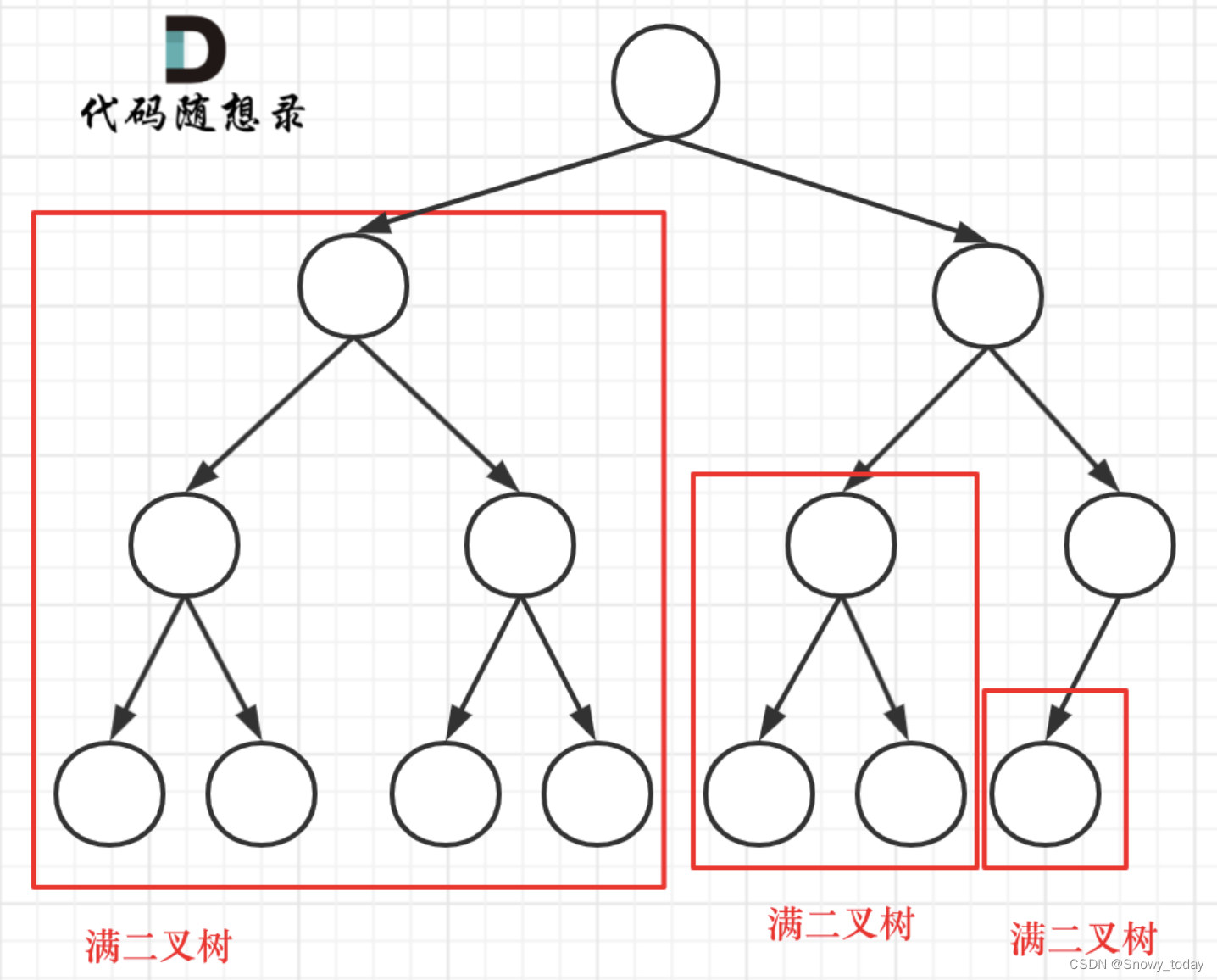
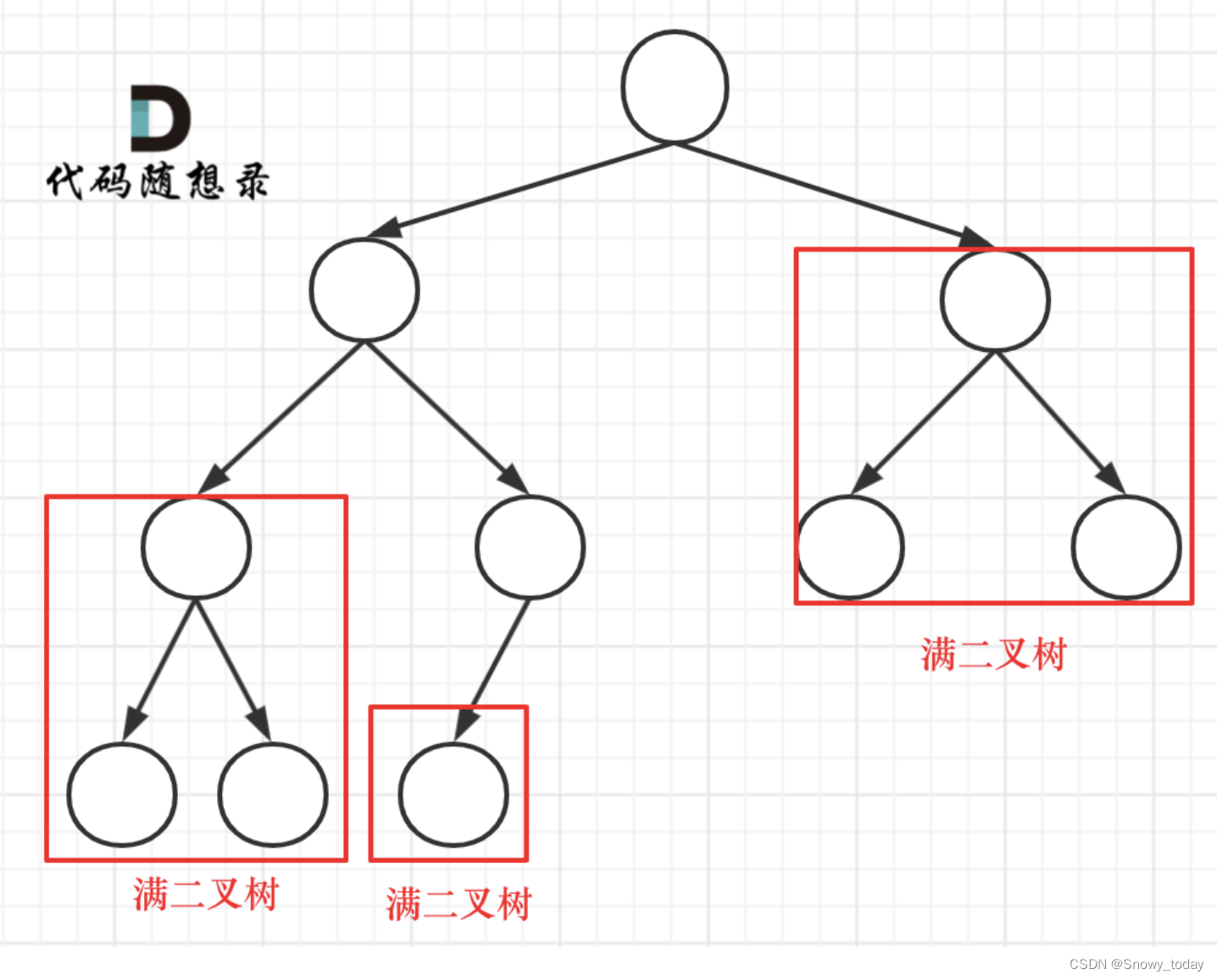
来自代码随想录

来自代码随想录

那么如何判断是否是满二叉树呢？
既然非满二叉树的完全二叉树只有可能是最后一层按照从左往右的顺序右边没有填满，那么只要查看一个树的最后一层的最左边的深度和最后一层的最右边的深度是否一样，就可以判断它是不是满的。

那么总结一下方法：就是往下递归找到最大块的满二叉树组成部分，来计算总共的节点数。

class Solution(object):
    def getFullHeight(self, root):
        # return -1 if it is not full
        # else, return the height of the full binary tree
        if not root:
            return 0
        left = 1
        right = 1
        lefttmp = root
        righttmp = root
        while lefttmp.left:
            lefttmp = lefttmp.left
            left += 1
        while righttmp.right:
            righttmp = righttmp.right
            right += 1
        if left == right:
            return left
        return -1 
        
        
    def countNodes(self, root):
        if not root:
            return 0
        h = self.getFullHeight(root)
        if h == -1:
            return 1 + self.countNodes(root.left) + self.countNodes(root.right)
        return 2**h - 1

优解参考简化：

优化一：代码量精简

class Solution: # 利用完全二叉树特性
    def countNodes(self, root: TreeNode) -> int:
        if not root: return 0
        count = 1
        left = root.left; right = root.right
        while left and right:
            count+=1
            left = left.left; right = right.right
        if not left and not right: # 如果同时到底说明是满二叉树，反之则不是
            return 2**count-1
        return 1+self.countNodes(root.left)+self.countNodes(root.right)

优化二：将getFullHeight的操作明确只对剩下的一半进行，让另一半以O(1)的复杂度完成，不需要再判断一次满二叉树了。

class Solution:
       def countNodes(self, root):
           if not root:
               return 0
           leftDepth = self.getDepth(root.left)
           rightDepth = self.getDepth(root.right)
           if leftDepth == rightDepth:
               return pow(2, leftDepth) + self.countNodes(root.right)
           else:
               return pow(2, rightDepth) + self.countNodes(root.left)
   
       def getDepth(self, root):
           if not root:
               return 0
           return 1 + self.getDepth(root.left)

Complexity
time: O(log n × log n)
space: O(log n)

时间复杂度的解释：
H为整个树的高度，n为总节点数。

判断是否为满二叉树及其深度的时间复杂度为O(H) = O(log n) 【getFullHeight】
从上面两种由满二叉树构成完全二叉树的方式中可以看出，root.right只有两种可能的高度，H-1或H-2
- H-1：少的这个高度就是root那一层，则root.left和root.right相同高度。也就是说，root.left一定是满二叉树，只需要O(1)就可以算出节点数，root.right需要进一步递归判断节点数。
- H-2：不仅少了root一层的高度，root.left比root.right高一层。也就是说最后一层不满的叶子结点全部都在root.left的范围里面，需要进一步递归判断节点数，而root.right是一个满二叉树，只需要O(1)就可以算出节点数。
从最后优化版中可以看到，在H层中，递归到每一层的时候，都有一半是满二叉树，可以用O(1) 的方式直接计算出数量，只需要进行一次【getFullHeight】，即对于O(log n)层，每一层进行一次O(log n)的操作，复杂度为 O(log n × log n)