Unity Shader之数学篇

一、坐标系

1、二维笛卡尔坐标系

屏幕坐标系是二维笛卡尔坐标系，OpenGL的屏幕坐标系原点在左下角，DirectX的屏幕坐标系原点在左上角。

2、三维笛卡尔坐标系

三维笛卡尔坐标系要区分是左手坐标系还是右手坐标系。

左手坐标系：举起你的左手，用食指和大拇指摆出一个“L”的手势，并且让你的食指指向上，大拇指指向右，现在伸出你的中指指向前方。大拇指指向就是x的正向，食指指向就是y的正向，中指指向就是z的正向。

右手坐标系：同上，改为右手操作。

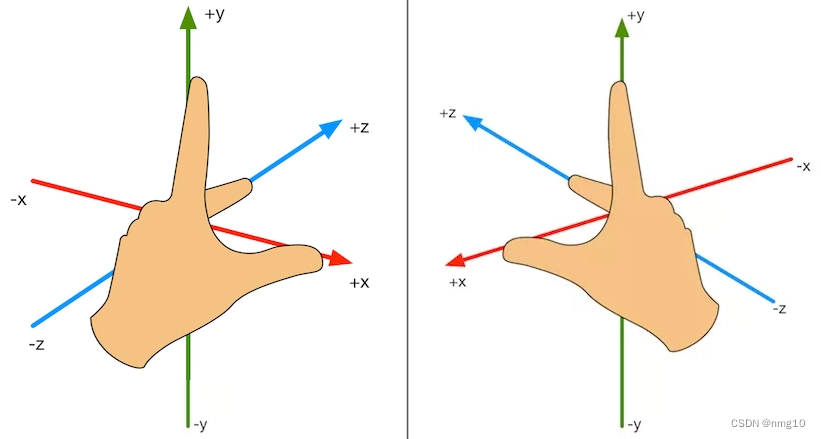
左手坐标系和右手坐标系对于正向旋转的定义也不同。

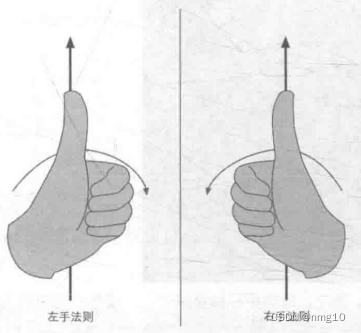
左手法则和右手法则

左手法则：伸出左手，大拇指指向旋转轴的正向，四指弯曲的方向就是旋转的正向。

右手法则：伸出右手，大拇指指向旋转轴的正向，四指弯曲的方向就是旋转的正向。

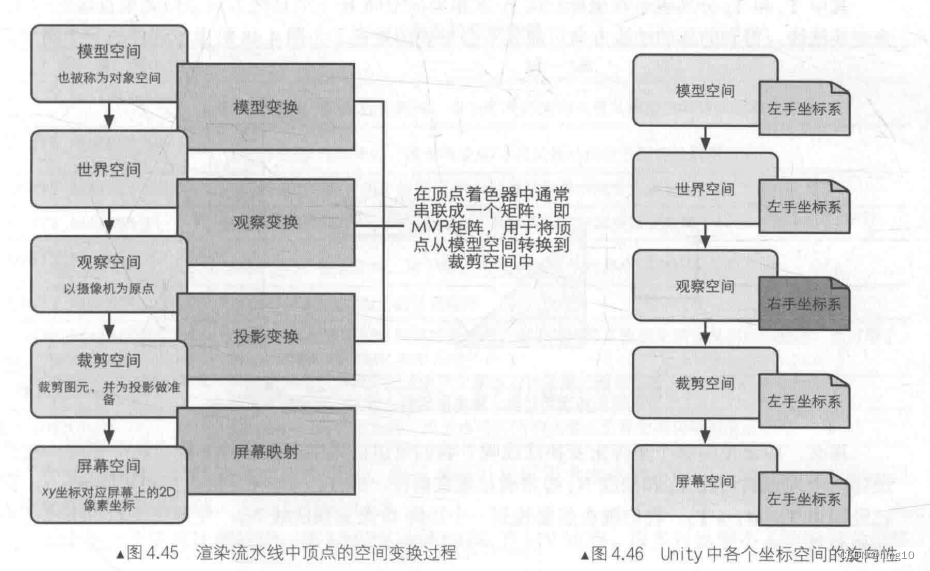
Unity的模型空间和世界空间使用的是左手坐标系。

Unity的观察空间（摄像机的坐标系）使用的是右手坐标系。

二、点和矢量

1、概念

点是n维空间中是一个位置，它没有大小概念。

矢量是包含大小和方向的有向线段。

标量用小写字母表示。

矢量用小写的粗体字母表示。

2、矢量运算

2.1 矢量和标量的乘除法

$k\vec{v}=(kv_x, kv_y, kv_z)$

$\tfrac{\vec{v}}{k} = ( \tfrac{x}{k}, \tfrac{y}{k}, \tfrac{z}{k} ) ( k\neq 0)$

2.2 矢量的加减法

$\vec a + \vec b = (a_x+b_x, a_y+b_y, a_z+b_z)$

$\vec a - \vec b = (a_x-b_x, a_y-b_y, a_z-b_z)$

2.3 矢量的模

$\left | \vec v \right | = \sqrt{v_{x}^{2} + v_{y}^{2} + v_{z}^{2}}$

2.4 单位矢量

$\hat{v} = \frac{\vec v}{\left | \vec v \right |} , \vec v$ 是非零矢量

2.5 矢量的点积

公式一： $\vec a\cdot \vec b = a_xb_x+a_yb_y+a_zb_z$

公式二： $\vec a\cdot \vec b =\left | \vec a \right | \left | \vec b \right |\cos \theta$

几何意义：是a向量在b向量上的投影的乘积，也可表示两个向量之间的夹角。

2.6 矢量的叉积

$\vec a\times \vec b =(a_yb_z-a_zb_y, a_zb_x-a_xb_z,a_xb_y-a_yb_x)$ 结果还是一个矢量，方向是使用对应坐标系的法则来确定。

3、练习题

3.1 假设，场景中有一个NPC，它位于点A处，它的前方可以用矢量 $\vec v$ 来表示。

问题1：如果现在玩家运动到了点B处，那么如何判断玩家是在NPC的前方还是后方。

答：用点积来判断，结果大于0就在前方。 $\overrightarrow{AB} \cdot \vec v$

问题2：现在NPC只能观察到有限的视角范围 $\phi$ 且视距为s，也就是说NPC最多只能看到它前方左侧或右侧 $\frac{\phi }{2}$ 角度内且相距在s范围内的物体。那么，我们如何通过点积来判断NPC是否可以看到点B呢？

答：首先求出AB的长度，如果大于s，则必定在视野外。如果小于等于s，则求 $\cos \theta$ ，根据 $\cos \theta = \frac{\vec a\cdot \vec b}{\left | \vec a \right | \left | \vec b \right |}$ 求得，然后判断 $\cos \theta$ 和 $\cos \frac{\phi }{2}$ 的大小关系，如果小于则在视野外，否则就在视野内。

3.2 在渲染中我们常会需要判断一个三角形片是正面还是背面，这可以通过判断三角形的3个顶点在当前空间中是顺时针还是逆时针排列来得到。

问题：已知三个点A、B、C，如何利用叉乘来判断。A、B、C都位于xy平面，人眼位于z轴的负方向上，向z轴正方向观察。

答： $\overrightarrow{AB}\times \overrightarrow{BC}=(0, 0, a)$

a如果大于0，则是逆时针，看到的是三角形的反面。

a如果小于0，则是顺时针，看到的是三角形的正面。

三、矩阵

1、定义

它是由 $m\times n$ 个标量组成的长方形数组。形如：

$\mathbf{M} = \begin{bmatrix} m_{11} &m_{12} &m_{13} \\ m_{21} &m_{22} &m_{23} \\ m_{31} &m_{32} &m_{33} \end{bmatrix}$

$m_{ij}$ 表明了这个元素在矩阵M的第i行、第j列。

2、矩阵运算

2.1 矩阵和标量的乘法

$k\mathbf{M} = \mathbf{M}k = \begin{bmatrix} km_{11} &km_{12} &km_{13} \\ km_{21} &km_{22} &km_{23} \\ km_{31} &km_{32} &km_{33} \end{bmatrix}$

2.2 矩阵和矩阵的乘法

一个 $r\times n$ 的矩阵A和一个 $n\times c$ 的矩阵B相乘，它们的结果AB将会是一个 $r\times c$ 大小的矩阵。

第一个矩阵的列数必须和第二行矩阵的行数相同，相乘得到的矩阵的行数是第一个矩阵的行数，而列数是第二个矩阵的列数。

相乘得到的矩阵C中的每个元素 $c_{ij}$ 等于A的第i行所对应的矢量和B的第j列所对应的矢量进行矢量点乘的结果。即

$c_{ij}=a_{i1}b_{1j}+a_{i2}b_{2j}+\cdots +a_{in}b_{nj}=\sum_{k=1}^{n}a_{ik}b_{kj}$

性质：矩阵乘法不满足交换律，满足结合律

3、特殊矩阵

3.1 方块矩阵

方块矩阵简称方阵，是指那些行和列数目相等的矩阵。

对角元素：指的是行号和列号相等的元素，如 $m_{11}$ 、 $m_{22}$ 、 $m_{33}$ 等。

对角矩阵：指的是一个方阵除了对角元素外的所有元素都为0的矩阵。

3.2 单位矩阵

一个特殊的对角矩阵，它的对角元素全为1，用 $\mathbf{I_{n}}$ 来表示。如下：

$\mathbf{I_{3}} = \begin{bmatrix} 1 &0 &0 \\ 0 &1 &0 \\ 0 &0 &1 \end{bmatrix}$

任何矩阵和它相乘的结果还是原来的矩阵。MI=IM=M

这就跟标量中的数字1一样。

3.3 转置矩阵

转置矩阵实际是对原矩阵的一种运算。给定一个 $r\times c$ 的矩阵M，它的转置可以表示成 $M^{T}$ ，这是一个 $c\times r$ 的矩阵。

转置矩阵的计算就是将原矩阵翻转一下即可。原矩阵的第i行变成了第i列，而第j列变成了第j行。公式如下：

$M_{ij}^{T} = M_{ji}$

性质一：矩阵转置的转置等于原矩阵。

$(M^{T})^{T}=M$

性质二：矩阵串接的转置，等于反向串接各个矩阵的转置。

$(AB)^{T}=B^{T}A^{T}$

3.4 逆矩阵

不是所有的矩阵都有逆矩阵，第一个前提就是，该矩阵必须是一个方阵。

给定一个方阵M，它的逆矩阵用 $M^{-1}$ 来表示。逆矩阵的重要性质就是，原矩阵与逆矩阵相乘结果是一个单位矩阵。

$MM^{-1}=M^{-1}M=I$

性质一：逆矩阵的逆矩阵是原矩阵。

$(M^{-1})^{-1}=M$

性质二：单位矩阵的逆矩阵是它本身。

$I^{-1}=I$

性质三：转置矩阵的逆矩阵是逆矩阵的转置。

$(M^{T})^{-1}=(M^{-1})^{T}$

性质四：矩阵串接相乘后的逆矩阵等于反向串接各个矩阵的逆矩阵。

$(AB)^{-1}=B^{-1}A^{-1}$

逆矩阵的几何意义：当我们使用变换矩阵 $M$ 对矢量 $\vec{v}$ 进行了一次变换，然后再使用它的逆矩阵 $M^{-1}$ 进行另一次变换，那么会得到原来的矢量。

$M^{-1}(M\vec v)=(M^{-1}M)\vec v=I\vec v=\vec v$

逆矩阵的计算：

方法一：伴随矩阵法

求伴随矩阵：对于n阶矩阵A，其伴随矩阵 $A^*$ 的元素 $A_{ij}^{*}$ 是 $\left | A_{ji} \right |$ ，其中 $A_{ji}$ 是去掉A中第j行第i列后得到的n-1阶子矩阵。
求行列式：计算矩阵A的行列式∣A∣。
计算逆矩阵： $A^{-1}=\frac{1}{\left | A \right |}A^{*}$ 。

方法二：初等变换法

构造增广矩阵：将原矩阵A与单位矩阵I放在一起，形成增广矩阵[A∣I]。
进行初等行变换：对增广矩阵[A∣I]进行初等行变换，目标是使左边的矩阵变为单位矩阵E。
提取逆矩阵：经过初等行变换后，增广矩阵变为[E∣B]，此时B即为A的逆矩阵 $A^{-1}$ 。

下面是一个简单的例子来说明如何使用初等变换法求逆矩阵：

假设矩阵 $A=\begin{bmatrix} 1 &2 \\ 3&4 \end{bmatrix}$ ，我们需要求其逆矩阵。

构造增广矩阵： $\begin{bmatrix} A|I \end{bmatrix} = \begin{bmatrix} 1 & 2 &1 &0 \\ 3& 4 &0 &1 \end{bmatrix}$ 。
进行初等行变换：
第一行乘以-3加到第二行： $\begin{bmatrix} 1 &2 &1 &0 \\ 0&-2 &-3 &1 \end{bmatrix}$ 。
第二行除以-2： $\begin{bmatrix} 1 &2 &1 &0 \\ 0&1 &\frac{3}{2} &-\frac{1}{2} \end{bmatrix}$ 。
第二行乘以-2加到第一行： $\begin{bmatrix} 1 &0 &-2 &1 \\ 0&1 &\frac{3}{2} &-\frac{1}{2} \end{bmatrix}$ 。
提取逆矩阵：经过初等行变换后，增广矩阵变为[E∣B]，其中B= $\begin{bmatrix} -2 &1 \\ \frac{3}{2} &-\frac{1}{2} \end{bmatrix}$ 即为A的逆矩阵 $A^{-1}$ 。

所以，矩阵A的逆矩阵为 $A^{-1}=\begin{bmatrix} -2 &1 \\ \frac{3}{2} &-\frac{1}{2} \end{bmatrix}$ 。

3.5 正交矩阵

如果一个方阵 $M$ 和它的转置矩阵的乘积是单位矩阵的话，我们就说这个矩阵是正交的。反过来说也是成立的。

$MM^T=M^TM=I$

如果一个矩阵是正交的，那么它的转置矩阵和逆矩阵是一样的。

$M^T=M^{-1}$

正交矩阵的特点：

$M^TM=\begin{bmatrix} - & c_1& -\\ - &c_2& -\\ - &c_3& - \end{bmatrix}\begin{bmatrix} | & |& |\\ c_1 &c_2& c_3\\ | &|& | \end{bmatrix}$

$=\begin{bmatrix} c_1\cdot c_1 &c_1\cdot c_2 &c_1\cdot c_3 \\ c_2\cdot c_1 &c_2\cdot c_2 &c_2\cdot c_3 \\ c_3\cdot c_1 &c_3\cdot c_2 &c_2\cdot c_3 \end{bmatrix}=\begin{bmatrix} 1 &0 &0 \\ 0&1 &0 \\ 0& 0& 1 \end{bmatrix}=I$

$c_1\cdot c_1=1,c_1\cdot c_2=0,c_1\cdot c_3=0 \newline c_2\cdot c_1=0,c_2\cdot c_2=1,c_2\cdot c_3=0 \newline c_3\cdot c_1=0,c_3\cdot c_2=0,c_3\cdot c_3=1$

我们可以得出以下结论：

1、矩阵的每一行，即 $c_1$ 、 $c_2$ 和 $c_3$ 是单位矢量，只有这样它们和自己的点积才能是1

2、矩阵的每一行，即 $c_1$ 、 $c_2$ 和 $c_3$ 之间相互垂直，只有这样它们之间的点积才能是0

3、上述结论对矩阵的每一列同样适用

因此，如果这些基矢量是一组标准正交基的话，那么我们就可以直接使用转置矩阵来求得该变换的逆变换。

4、行矩阵还是列矩阵

一个矢量可以转换成一个行矩阵或列矩阵。它本身没什么区别，但是，当我们把它和另一个矩阵相乘时，就会出现一些差异。

假设有一个矢量 $\vec v = (x,y,z)$ ，我们将它的行、列矩阵分别和矩阵 $M$ 相乘：

$M=\begin{bmatrix} m_{11} &m_{12} &m_{13} \\ m_{21} &m_{22} &m_{23} \\ m_{31} &m_{32} &m_{33} \end{bmatrix}$

和行矩阵相乘要放在矩阵 $M$ 的左边：

$\vec v M=[xm_{11}+ym_{21}+zm_{31},xm_{12}+ym_{22}+zm_{32},xm_{13}+ym_{23}+zm_{33}]$

和列矩阵相乘要放在矩阵 $M$ 的右边：

$M\vec v = \begin{bmatrix} xm_{11}+ym_{12}+zm_{13}\\ xm_{21}+ym_{22}+zm_{23}\\ xm_{31}+ym_{32}+zm_{33} \end{bmatrix}$

认真比较会发现，结果矩阵除了行列矩阵的区别外，里面的元素也是不一样的。这就意味着，在和矩阵相乘时选择行矩阵还是列矩阵来表示矢量是非常重要的，因为这决定了矩阵相乘法的书写次序和结果值。

在Unity中，常规做法是把矢量放在矩阵的右侧，即把矢量转换成列矩阵来进行运算。

5、矩阵的几何意义：变换

5.1 线性变换

指的是那些可以保留矢量加和标量乘的变换。用数学公式来表示这两个条件就是：

$f(\vec x)+f(\vec y)=f(\vec x+\vec y) \newline \newline kf(\vec x)=f(k\vec x)$

缩放就是一种线性变换。例如 $f(\vec x)=2\vec x$ ，可以表示一个大小为2的统一缩放。可以发现， $f(\vec x)=2\vec x$ 是满足上述两个条件的。

线性变换包括：旋转、缩放、错切、镜像、正交投影等。

仅有线性变换时不够的，平移变换就不是一个线性变换，例如 $f(\vec x)=\vec x+(1,2,3)$ ，它满足标量乘法，但不满足矢量加法。

如果令 $\vec x = (1,1,1)$ ，那么：

$f(\vec x)+f(\vec x)=(4,6,8) \newline \newline f(\vec x+\vec x)=(3,4,5)$

可见，两个运算得到的结果是不一样的。因此，不能用一个3x3的矩阵来表示一个平移变换。这样就有了仿射变换。

5.2 仿射变换

是合并线性变换和平移变换的变换类型。仿射变换可以使用一个4x4的矩阵来表示，为此，我们需要把矢量扩展到四维空间下，这就是齐次坐标空间。

下表给出了图形学中常见变换矩阵的名称和它们的特性。

5.3 齐次坐标

由于3x3的矩阵不能表示平移操作，那么就将其扩展到了4x4的矩阵。为此，我们还需要把原来的三维矢量转换成四维矢量，也就是我们所说的齐次坐标（齐次坐标的维度可以超过四维，本文所说的齐次坐标泛指四维齐次坐标）。

对于一个点，从三维坐标转换成齐次坐标是把其w分量设为1，而对于方向矢量来说，需要把其分量设为0。这样设置会导致，当用一个4x4矩阵对一个点进行变换时，平移、旋转、缩放都会施加于该点，但是如果是用于一个方向矢量，平移效果就会被忽略。

5.3.1 分解基础变换矩阵

把表示纯平移、纯旋转和纯缩放的变换矩阵叫做基础变换矩阵。这些矩阵具有一些共同点，我们可以把一个基础变换矩阵分解成4个组成部分：

$\begin{bmatrix} M_{3\times 3} &t_{3\times 1} \\ 0_{1\times 3} &1 \end{bmatrix}$

其中，左上角的矩阵 $M_{3\times 3}$ 用于表示旋转和缩放， $t_{3\times 1}$ 用于表示平移， $0_{1\times 3}$ 是零矩阵，右下角的元素就是标量1。

5.3.2 平移矩阵

对点做平移变换：

$\begin{bmatrix} 1 &0 &0 &t_x \\ 0&1 &0 &t_y \\ 0&0 &1 &t_z \\ 0&0 &0 &1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}=\begin{bmatrix} x+t_x\\ y+t_y\\ z+t_z\\ 1 \end{bmatrix}$

对矢量做平移变换：

$\begin{bmatrix} 1 &0 &0 &t_x \\ 0&1 &0 &t_y \\ 0&0 &1 &t_z \\ 0&0 &0 &1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 0 \end{bmatrix}=\begin{bmatrix} x\\ y\\ z\\ 0 \end{bmatrix}$

显而易见，平移变换不会对矢量产生任何影响。这点很容易理解，前面已经说过矢量是没有位置属性的。

平移矩阵的逆矩阵就是反向平移得到的矩阵：

$\begin{bmatrix} 1 &0 &0 &-t_x \\ 0&1 &0 &-t_y \\ 0&0 &1 &-t_z \\ 0&0 &0 &1 \end{bmatrix}$

平移矩阵并不是一个正交矩阵。

5.3.3 缩放变换

对一个模型沿空间的x轴、y轴、z轴进行缩放变换：

$\begin{bmatrix} k_x &0 &0 &0 \\ 0&k_y &0 &0 \\ 0&0 &k_z &0 \\ 0&0 &0 &1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 1 \end{bmatrix}=\begin{bmatrix} k_xx\\ k_yy\\ k_zz\\ 1 \end{bmatrix}$

对矢量进行缩放变换：

$\begin{bmatrix} k_x &0 &0 &0 \\ 0&k_y &0 &0 \\ 0&0 &k_z &0 \\ 0&0 &0 &1 \end{bmatrix}\begin{bmatrix} x\\ y\\ z\\ 0 \end{bmatrix}=\begin{bmatrix} k_xx\\ k_yy\\ k_zz\\ 0 \end{bmatrix}$

如果缩放系数 $k_x=k_y=k_z$ ，这样的缩放称为统一缩放，否则称为非统一缩放。

缩放矩阵的逆矩阵是使用原缩放系数的倒数进行缩放变换：

$\begin{bmatrix} \frac{1}{k_x} &0 &0 &0 \\ 0&\frac{1}{k_y} &0 &0 \\ 0&0 &\frac{1}{k_z} &0 \\ 0&0 &0 &1 \end{bmatrix}$

缩放矩阵一般不是正交矩阵。上面的矩阵只适用于沿坐标轴方向进行缩放。如果沿任意方向进行缩放，就需要使用一个复合变换。其中一种方法的主要思想就是：先将缩放轴变换成标准坐标轴，然后进行沿坐标轴的缩放，再进行逆变换得到原来的缩放轴朝向。

5.3.4 旋转矩阵

旋转矩阵是三种常见的变换矩阵中最复杂的一种。旋转操作需要指定一个旋转轴，这个旋转轴不一定是空间的坐标轴，下面列举的是围绕空间的x轴、y轴、z轴进行旋转。

将点绕着x轴旋转 $\theta$ 度：

$R_x(\theta )=\begin{bmatrix} 1 &0 &0 &0 \\ 0&\cos \theta &-\sin \theta &0 \\ 0&\sin \theta &\cos \theta &0 \\ 0&0 &0 &1 \end{bmatrix}$

将点绕着y轴旋转 $\theta$ 度：

$R_y(\theta )=\begin{bmatrix} \cos \theta &0 &\sin \theta &0 \\ 0&1 &0 &0 \\ -\sin \theta&0 &\cos \theta &0 \\ 0&0 &0 &1 \end{bmatrix}$

将点绕着z轴旋转 $\theta$ 度：

$R_z(\theta )=\begin{bmatrix} \cos \theta &-\sin \theta &0 &0 \\ \sin \theta&\cos \theta &0 &0 \\ &0 &1 &0 \\ 0&0 &0 &1 \end{bmatrix}$

旋转矩阵的逆矩阵是旋转相反角度得到的变换矩阵。旋转矩阵是正交矩阵，而且多个旋转矩阵之间的串联同样是正交的。

5.3.5 复合变换

复合变换就是把平移、旋转和缩放组合起来，形成一个复杂的变换过程。

复合变换可以通过矩阵的串联来实现。例如先缩放、再旋转、最后平移，可以表示如下：

$P_{new} = M_{tran}M_{rotation}M_{scale}P_{old}$

由于我们使用的是列矩阵，因此阅读顺序是从右到左的。

为了从数学公式上理解变换顺序的本质，我们可以对比不同变换顺序产生的变换矩阵的表达式。

如果我们只考虑对y轴的旋转的话，按先缩放、再旋转、最后平移这样的顺序组合3种变换得到的变换矩阵是：

$M_{tran}M_{y }(\theta)M_s=\begin{bmatrix} 1 &0 &0 &t_x \\ 0&1 &0 &t_y \\ 0&0 &1 &t_z \\ 0&0 &0 &1 \end{bmatrix}\begin{bmatrix} \cos\theta &0 &\sin\theta &0 \\ 0&1 &0 &0 \\ -\sin\theta &0 &\cos\theta &0 \\ 0& 0& 0& 1 \end{bmatrix}\begin{bmatrix} k_x &0 &0 &0 \\ 0&k_y &0 &0 \\ 0&0 &k_z &0 \\ 0& 0 &0 &1 \end{bmatrix} \newline \newline \newline =\begin{bmatrix} k_x\cos\theta & 0 &k_z\sin\theta &t_x \\ 0&k_y &0 &t_y \\ -k_x\sin\theta &0 &k_z\cos\theta &-t_z \\ 0&0 &0 &1 \end{bmatrix}$

而如果我们使用其他变换顺序，例如先平移，再缩放，最后旋转，那么得到的变换矩阵是：

$M_{y }(\theta)M_sM_{tran}= \begin{bmatrix} \cos\theta &0 &\sin\theta &0 \\ 0&1 &0 &0 \\ -\sin\theta &0 &\cos\theta &0 \\ 0& 0& 0& 1 \end{bmatrix} \begin{bmatrix} k_x &0 &0 &0 \\ 0&k_y &0 &0 \\ 0&0 &k_z &0 \\ 0& 0 &0 &1 \end{bmatrix} \begin{bmatrix} 1 &0 &0 &t_x \\ 0&1 &0 &t_y \\ 0&0 &1 &t_z \\ 0&0 &0 &1 \end{bmatrix} \newline \newline \newline =\begin{bmatrix} k_x\cos\theta & 0 &k_z\sin\theta &t_xk_x\cos\theta+t_zk_z\sin\theta \\ 0&k_y &0 &t_xk_x \\ -k_x\sin\theta &0 &k_z\cos\theta &-t_xk_x\sin\theta+t_zk_z\cos\theta \\ 0&0 &0 &1 \end{bmatrix}$

从两个结果可以看出，得到的变换矩阵是不一样的。

除了需要注意不同类型的变换顺序外，还要小心旋转的变换顺序。当我们给出了分别绕x轴、y轴和z轴旋转的变换矩阵。一个问题是，它们的顺序如何定义呢？

在Unity中，这个旋转顺序是zxy，这在旋转相关的API文档中都有说明。

旋转角度 $(\theta _x,\theta _y,\theta _z)$ ：

$\bullet$ 绕坐标系E下的z轴旋转 $\theta _z$ ，绕坐标系E下的y轴旋转 $\theta _y$ ，绕坐标系E下的x轴旋转 $\theta _x$ ，即进行一次旋转时不一起旋转当前坐标系。

5.3.6 法线变换

法线也被称为法矢量。法线变换是一种特殊的变换。

使用原变换矩阵的逆转置矩阵来变换法线就可以得到正确的结果。值得注意的事，如果变换矩阵 $M_{A \to B}$ 是正交矩阵，那么 $M_{A \to B}^{-1}=M_{A \to B}^{T}$ ，因此 $(M_{A \to B}^{T})^{-1}=M_{A \to B}$ ，也就是说我们可以使用用于变换顶点的变换矩阵来直接变换法线。

1、如果变换只包括旋转变换，那么这个变换矩阵就是正交矩阵，可以用于法线变换。

2、如果变换只包含旋转和统一缩放，而不包含非统一缩放，可以将变换矩阵乘以 $\frac{1}{k}$ 用于法线变换。

3、如果变换包含了非统一变换，那么我们就必须要求解逆矩阵来得到变换法线的矩阵

四、坐标空间

坐标空间必须指明原点位置和3个坐标轴的方向。每个坐标空间都是另一个坐标空间的子空间。

现在，我们已知子空间 $C$ 的3个坐标轴在父空间 $P$ 下的表示 $x_c$ 、 $y_c$ 、 $z_c$ ，以及原点位置 $O_c$ 。当给定一个子坐标空间中的一点 $A_c=(a,b,c)$ ，我们可以确定其在父坐标空间下的位置 $A_p$ ：

1、从坐标空间的原点开始

$O_c$

2、向x轴方向移动a个单位

$O_c+ax_c$

3、向y轴方向移动b个单位

$O_c+ax_c+by_c$

4、向z轴方向移动c个单位

$O_c+ax_c+by_c+cz_c$

现在，我们已经求出了 $A_p$ ：

$A_p=O_c+ax_c+by_c+cz_c$

子坐标空间到父坐标空间的变换矩阵，记为 $M_{c \rightarrow p}$

$M_{c \rightarrow p}=\begin{bmatrix} | &| &| &| \\ x_c &y_c &z_c &O_c \\ |& | & | &| \\ 0& 0& 0& 1 \end{bmatrix}$

对矢量的坐标空间变换可以使用3x3的矩阵表示：

$M_{c \rightarrow p}=\begin{bmatrix} | &| &| \\ x_c &y_c &z_c\\ |& | & | \end{bmatrix}$

1、模型空间

也被称为对象空间或局部空间。每个模型都有自己独立的坐标空间，当它移动或旋转的时候，模型空间也会跟着它移动和旋转。

在Unity在中，模型空间中使用的是左手坐标系。

模型空间的原点和坐标轴通常是由美术人员在建模软件里确定好的。

2、世界空间

它是一个特殊的坐标系，因为它建立了我们所关心的最大的空间。

在Unity在中，世界空间中使用的是左手坐标系。

顶点变换的第一步，就是将顶点坐标从模型空间变换到世界空间中。这个变换通常叫做模型变换。

3、观察空间

观察空间也被称为摄像机空间。

在Unity在中，观察空间中使用的是右手坐标系。

顶点变换的第二步，就是将顶点坐标从世界空间变换到观察空间中。这个变换通常叫做观察变换。

4、裁剪空间

顶点接下来要从观察空间转换到裁剪空间（也被称为齐次裁剪空间）中，这个用于变换的矩阵叫做裁剪矩阵，也被称为投影矩阵。

视椎体：决定裁剪空间的范围。视椎体由六个平面包围而成，这些平面也被称为裁剪平面。

视椎体有两种类型，这涉及两种投影类型：一种是正交投影，一种是透视投影。使用的矩阵叫投影矩阵。

5、屏幕空间

经过投影矩阵的变换后，就可以进行裁剪操作。当完成了所有的裁剪工作后，就需要进行真正的投影了，也就是将视椎体投影到屏幕空间中。

屏幕空间是一个二维空间。

首先，我们需要进行标准齐次除法，也被称为透视除法。就是用齐次坐标系的w分量去除以x、y、z分量。进过这一步后会将裁剪空间变到一个立方体内。

6、总结

五、Unity Shader的内置变量

内置着色器变量 - Unity 手册

1、变换

所有这些矩阵都是float4x4类型，并且是列主序的。

名称	值
UNITY_MATRIX_MVP	当前模型 * 视图 * 投影矩阵。用于将顶点/方向矢量从模型空间变换到裁剪空间
UNITY_MATRIX_MV	当前模型 * 视图矩阵。用于将顶点/方向矢量从模型空间变换到观察空间
UNITY_MATRIX_V	当前视图矩阵。用于将顶点/方向矢量从世界空间变换到观察空间
UNITY_MATRIX_P	当前投影矩阵。用于将顶点/方向矢量从观察空间变换到裁剪空间
UNITY_MATRIX_VP	当前视图 * 投影矩阵。用于将顶点/方向矢量从世界空间变换到裁剪空间
UNITY_MATRIX_T_MV	模型转置 * 视图矩阵。UNITY_MATRIX_MV的转置矩阵
UNITY_MATRIX_IT_MV	模型逆转置 * 视图矩阵。UNITY_MATRIX_MV的逆转置矩阵，用于将法线从模型空间变换到观察空间，也可用于得到UNITY_MATRIX_MV的逆矩阵
unity_ObjectToWorld	当前模型矩阵。用于将顶点/方向矢量从模型空间变换到世界空间
unity_WorldToObject	当前世界矩阵的逆矩阵。用于将顶点/方向矢量从世界空间变换到模型空间

2、摄像机和屏幕

这些变量将对应于正在渲染的摄像机。例如，在阴影贴图渲染中，它们仍将引用摄像机组件值，而不是用于阴影贴图投影的“虚拟摄像机”。

名称	类型	值
_WorldSpaceCameraPos	float3	摄像机的世界空间位置。
_ProjectionParams	float4	`x` 是 1.0（如果当前使用翻转投影矩阵进行渲染，则为 –1.0），`y` 是摄像机的近平面，`z` 是摄像机的远平面，`w` 是远平面的倒数。
_ScreenParams	float4	`x` 是摄像机目标纹理的宽度（以像素为单位），`y` 是摄像机目标纹理的高度（以像素为单位），`z` 是 1.0 + 1.0/宽度，`w` 为 1.0 + 1.0/高度。
_ZBufferParams	float4	用于线性化 Z 缓冲区值。`x` 是 (1-远/近)，`y` 是 (远/近)，`z` 是 (x/远)，`w` 是 (y/远)。
unity_OrthoParams	float4	`x` 是正交摄像机的宽度，`y` 是正交摄像机的高度，`z` 未使用，`w` 在摄像机为正交模式时是 1.0，而在摄像机为透视模式时是 0.0。
unity_CameraProjection	float4x4	摄像机的投影矩阵。
unity_CameraInvProjection	float4x4	摄像机投影矩阵的逆矩阵。
unity_CameraWorldClipPlanes[6]	float4	摄像机视锥体平面世界空间方程，按以下顺序：左、右、底、顶、近、远。

3、时间

时间以秒为单位，并由项目 Time 设置中的时间乘数 (Time multiplier) 进行缩放。没有内置变量可用于访问未缩放的时间。

名称	类型	值
_Time	float4	自关卡加载以来的时间 (t/20, t, t2, t3)，用于将着色器中的内容动画化。
_SinTime	float4	时间正弦：(t/8, t/4, t/2, t)。
_CosTime	float4	时间余弦：(t/8, t/4, t/2, t)。
unity_DeltaTime	float4	增量时间：(dt, 1/dt, smoothDt, 1/smoothDt)。

4、光照

光源参数以不同的方式传递给着色器，具体取决于使用哪个渲染路径，以及着色器中使用哪种光源模式通道标签。

前向渲染（ForwardBase 和 ForwardAdd 通道类型）：


名称	类型	值
_LightColor0（在 UnityLightingCommon.cginc 中声明）	fixed4	光源颜色。
_WorldSpaceLightPos0	float4	方向光：（世界空间方向，0）。其他光源：（世界空间位置，1）。
unity_WorldToLight（在 AutoLight.cginc 中声明）	float4x4	世界/光源矩阵。用于对剪影和衰减纹理进行采样。
unity_4LightPosX0、unity_4LightPosY0、unity_4LightPosZ0	float4	（仅限 ForwardBase 通道）前四个非重要点光源的世界空间位置。
unity_4LightAtten0	float4	（仅限 ForwardBase 通道）前四个非重要点光源的衰减因子。
unity_LightColor	half4[4]	（仅限 ForwardBase 通道）前四个非重要点光源的颜色。
unity_WorldToShadow	float4x4[4]	世界/阴影矩阵。聚光灯的一个矩阵，方向光级联最多有四个矩阵。

延迟着色和延迟光照，在光照通道着色器中使用（全部在 UnityDeferredLibrary.cginc 中声明）：


名称	类型	值
_LightColor	float4	光源颜色。
unity_WorldToLight	float4x4	世界/光源矩阵。用于对剪影和衰减纹理进行采样。
unity_WorldToShadow	float4x4[4]	世界/阴影矩阵。聚光灯的一个矩阵，方向光级联最多有四个矩阵。

为 ForwardBase、PrePassFinal 和 Deferred 通道类型设置了球谐函数系数（由环境光和光照探针使用）。这些系数包含由世界空间法线求值的三阶 SH 函数（请参阅 UnityCG.cginc 中的 ShadeSH9）。这些变量都是 half4 类型、unity_SHAr 和类似名称。

顶点光照渲染（Vertex 通道类型）：

最多可为 Vertex 通道类型设置 8 个光源；始终从最亮的光源开始排序。因此，如果您希望一次渲染受两个光源影响的对象，可直接采用数组中前两个条目。如果影响对象的光源数量少于 8，则其余光源的颜色将设置为黑色。


名称	类型	值
unity_LightColor	half4[8]	光源颜色。
unity_LightPosition	float4[8]	视图空间光源位置。方向光为 (-direction,0)；点光源/聚光灯为 (position,1)。
unity_LightAtten	half4[8]	光源衰减因子。x 是 cos(spotAngle/2) 或 –1（非聚光灯）；_y_ 是1/cos(spotAngle/4) 或 1（非聚光灯）；_z_ 是二次衰减；_w_ 是平方光源范围。
unity_SpotDirection	float4[8]	视图空间聚光灯位置；非聚光灯为 (0,0,1,0)。

5、光照贴图


名称	类型	值
unity_Lightmap	Texture2D	包含光照贴图信息。
unity_LightmapST	float4[8]	缩放 UV 信息并转换到正确的范围以对光照贴图纹理进行采样。

6、雾效和环境光


名称	类型	值
unity_AmbientSky	fixed4	梯度环境光照情况下的天空环境光照颜色。
unity_AmbientEquator	fixed4	梯度环境光照情况下的赤道环境光照颜色。
unity_AmbientGround	fixed4	梯度环境光照情况下的地面环境光照颜色。
UNITY_LIGHTMODEL_AMBIENT	fixed4	环境光照颜色（梯度环境情况下的天空颜色）。旧版变量。
unity_FogColor	fixed4	雾效颜色。
unity_FogParams	float4	用于雾效计算的参数：(density / sqrt(ln(2))、density / ln(2)、–1/(end-start) 和 end/(end-start))。x 对于 Exp2 雾模式很有用；_y_ 对于 Exp 模式很有用，_z_ 和 w 对于 Linear 模式很有用。

7、其他


名称	类型	值
unity_LODFade	float4	使用 LODGroup 时的细节级别淡入淡出。x 为淡入淡出（0 到 1），_y_ 为量化为 16 级的淡入淡出，_z_ 和 w 未使用。
_TextureSampleAdd	float4	根据所使用的纹理是 Alpha8 格式（值设置为 (1,1,1,0)）还是不是该格式（值设置为 (0,0,0,0)）由 Unity 仅针对 UI 自动设置。

六、答疑解惑

1、使用3x3还是4x4的变换矩阵

对于线性变换（例如旋转和缩放）来说，仅使用3×3的矩阵就足够表示所有的变换了。但如果存在平移变换，我们就需要使用4x4的矩阵。因此，在对顶点的变换中，我们通常使用4x4的变换矩阵。当然，在变换前我们需要把点坐标转换成齐次坐标的表示，即把顶点的W分量设为1。而在对方向失量的变换中，我们通常使用3×3的矩阵就足够了，这是因为平移变换对方向失量是没有影响的。

2、CG中的矢量和矩阵类型

我们通常在Unity Shader中使用CG作为着色器编程语言。在CG中变量类型有很多种，但在本节我们是想解释如何使用这些类型进行数学运算。因此，我们只以float家族的变量来做说明。
在CG中，矩阵类型是由float3x3、float4x4等关键词进行声明和定义的。而对于float3、float4
等类型的变量，我们既可以把它当成一个矢量，也可以把它当成是一个1xn的行矩阵或者一个n
x1的列矩阵。这取决于运算的种类和它们在运算中的位置。例如，当我们进行点积操作时，两个
操作数就被当成失量类型，如下：

float4 a = float4(1.0, 2.0, 3.0, 4.0);
float4 b = float4(1.0, 2.0, 3.0, 4.0);
//对两个失量进行点积操作
float result = dot(a, b);

但在进行矩阵乘法时，参数的位置将决定是按列矩阵还是行矩阵进行乘法。在CG中，矩阵乘法是通过mul函数实现的。例如：
float4 v = float4(1.0, 2.0, 3.0, 4.0);
float4x4 M = float4x4(1.0, 0.0, 0.0, 0.0,
0.0, 1.0, 0.0, 0.0
0.0, 0.0, 1.0, 0.0,
0.0, 0.0, 0.0, 1.0);
//把v当成列矩阵和矩阵M进行右乘
float4 column_mul_result = mul(M, v);
//把v当成行矩阵和矩阵M进行左乘
float4 row_mul_result = mul(v, M);
//注意：column_mul_result不等于row_mul_result，而是
// mul (M, v) == mul (v, tranpose(M))
// mul (v, M) == mul (tranpose(M), v)

因此，参数的位置会直接影响结果值。通常在变换顶点时，我们都是使用右乘的方式来按列矩阵进行乘法。这是因为，Unity提供的内置矩阵（如UNITY_MATRIX_MVP等）都是按列存储的。但有时，我们也会使用左乘的方式，这是因为可以省去对矩阵转置的操作。
需要注意的一点是，CG对矩阵类型中元素的初始化和访间顺序。在CG中，对float4x4等类型的变量是按行优先的方式进行填充的。什么意思呢？我们知道，想要填充一个矩阵需要给定一串数学，例如，如果需要声明一个3×4的矩阵，我们需要提供12个数字。那么，这串数字是一行一行地填充矩阵还是一列一列地填充矩阵呢？这两种方式得到的矩阵是不同的。例如，我们使用(1, 2, 3, 4, 5, 6, 7,8, 9)去填充一个3×3的矩阵，如果是按照行优先的方式，得到的矩阵是：

$\begin{bmatrix} 1 & 2 &3 \\ 4&5 &6 \\ 7& 8 &9 \end{bmatrix}$

如果是按照列优先的方式，得到的矩阵是：

$\begin{bmatrix} 1 &4 &7 \\ 2 & 5 &8 \\ 3& 6 &9 \end{bmatrix}$

CG使用的是行优先的方法，即是一行一行地填充矩阵的。因此，如果读者需要自已定义一个矩阵时（例如，自已构建用于空间变换的矩阵），就要注意这里的初始化方式。
类似地，当我们在CG中访问一个矩阵中的元素时，也是按行来索引的。例如

//按行优先的方式初始化矩阵M
float3x3 M = float3x3(1.0, 2.0, 3.0,
4.0, 5.0, 6.0,
7.0, 8.0, 9.0);
//得到M的第一行，即（1.0, 2.0, 3.0）
float3 row = M[0];
//得到M的第2行第1列的元素，即4.0
float ele = M[1][0];

之所以Unity Shader中的矩阵类型满足上述规则，是因为使用的是CG语言。换句话说，上
面的特性都是CG的规定。
如果读者熟悉Unity的API，可能知道Unity在脚本中提供了一种矩阵类型Matrix4x4。脚本中的这个矩阵类型则是采用列优先的方式。这与Unity Shader中的规定不一样，希望读者在遇到时不会感到困惑。

3、Unity中的屏幕坐标：ComputeScreenPos/VPOS/WPOS

在写 Shader 的过程中，我们有时候希望能够获得片元在屏幕上的像素位置。在顶点/片元看色器中，有两种方式来获得片元的屏幕坐标。
一种是在片元着色器的输入中声明VPOS或WPOS语义（关于什么是语义，可参见5.4节）VPOS是HLSL中对屏幕坐标的语义，而WPOS 是CG 中对屏幕坐标的语义。两者在Unity Shader
中是等价的。我们可以在HLSL/CG 中通过语义的方式来定义顶点/片元着色器的默认输入，而不
需要目已定义输人输出的数据结构。这里的内容有一些超前，因为我们还没有具体讲解顶点/片元
看色器的写法，读者在这里可以只关注VPOS和 WPOS的语义。使用这种方法，可以在片元着色器中这样写：

fixed4 frag(float4 sp : VPOS) : SV_Target {
//用屏幕坐标除以屏幕分辨率 ScreenParams.xy，得到视口空间中的坐标
return fixed4 (sp.xy/_ScreenParams.xy, 0.0, 1.0);
}

另一种方式是通过Unity提供的ComputeScreenPos函数。

Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };

            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
            };

            
            struct vertOut{
                float4 pos :SV_POSITION;
                float4 scrPos : TEXCOORDO;
            };
            vertOut vert(appdata_base v) {
                vertOut o;
                o.pos = UnityObjectToClipPos (v.vertex);
                //第一步：把ComputeScreenPos 的结果保存到scrPos中
                o.scrPos = ComputeScreenPos (o.pos);
                return o;
            }
            fixed4 frag(vertOut i): SV_Target {
                //第二步：用scrPos.xy除以scrPos.w得到视口空间中的坐标
                float2 wcoord = (i.scrPos.xy/i.scrPos.w);
                return fixed4(wcoord,0.0,1.0);
            }
            ENDCG
        }

效果如下：

将上面的frag改成这样，会得到一个动态效果：

Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float2 uv : TEXCOORD0;
            };
            struct v2f
            {
                float2 uv : TEXCOORD0;
                float4 vertex : SV_POSITION;
            };

            v2f vert (appdata v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.uv = v.uv;
                return o;
            }
            fixed4 frag(v2f i): SV_Target {
                fixed3 col = 0.5 + 0.5*cos(_Time.y + i.uv.xyx + fixed3(0,2,4));
                return fixed4(col, 1.0);
            }
            ENDCG
        }