【Leetcode每日一题】动态规划 - 下降路径最小和（难度⭐⭐）（55）

news2024/9/21 4:34:40

1. 题目解析

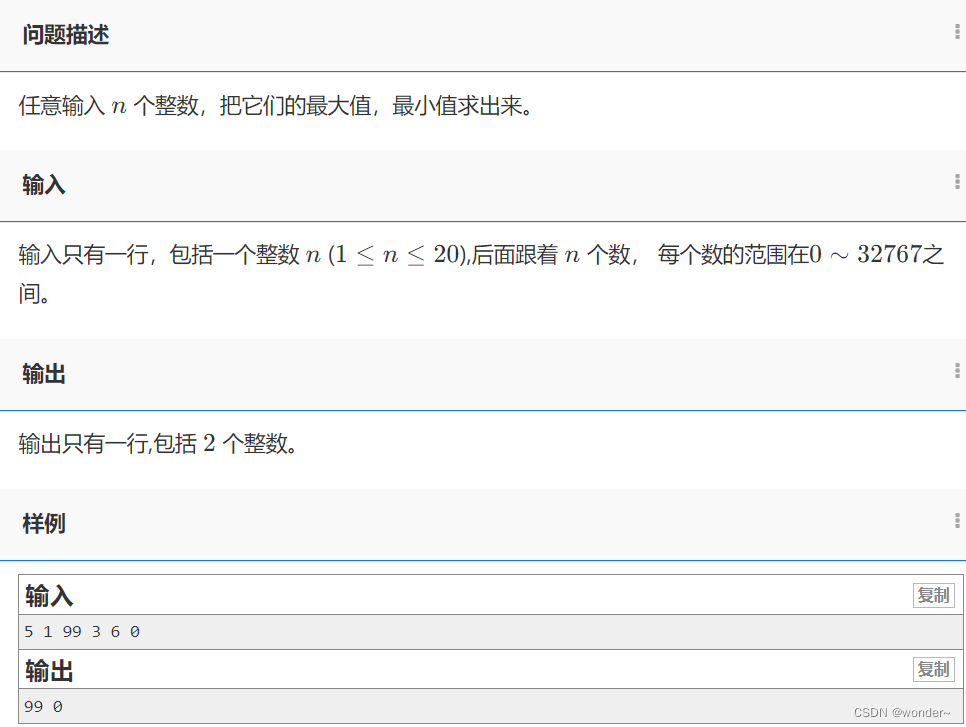
题目链接：931. 下降路径最小和

这个问题的理解其实相当简单，只需看一下示例，基本就能明白其含义了.

2.算法原理

对于这类路径类问题，通常我们首先需要分析状态表示以及状态转移的过程。特别地，本题涉及的是路径上的最小值累加，因此状态转移方程的设计尤为重要。

状态表示：
- 我们选择的状态表示方式为：dp[i][j] 代表到达位置 [i, j] 时，所有下降路径中的最小和。这种定义方式有助于我们后续的状态转移和结果求解。
状态转移方程：
- 对于位置 [i, j]，根据题目要求，我们可以从上方、左上方或右上方三个方向转移而来。我们需要找到这三个方向中的最小值，并加上当前位置 [i, j] 的值，从而得到到达该位置的最小路径和。
- 因此，状态转移方程为：dp[i][j] = min(dp[i - 1][j], min(dp[i - 1][j - 1], dp[i - 1][j + 1])) + matrix[i][j]。
初始化：
- 为了简化计算，我们可以在矩阵的上方额外添加一行辅助结点，并将其值初始化为0。这样做的好处在于，当我们计算第一行时，可以直接引用这些辅助结点的值，而无需进行额外的判断。
- 同时，考虑到状态转移时可能需要访问到 [i, j - 1] 和 [i, j + 1] 这样的位置，我们可能需要在矩阵的两侧也额外添加列，并初始化这些列的值。
- 通常情况下，这些辅助结点的值需要保证后续填表过程的正确性。在本题中，由于我们关心的是路径上的最小值累加，因此将辅助结点的值初始化为0是合理的。
填表顺序：
- 根据状态表示和状态转移方程，我们可以确定填表的顺序是从上往下逐行计算。这样做的原因是，在计算当前行的某个位置时，我们只需要依赖上一行的数据，这符合动态规划的自底向上思想。
返回值：
- 题目要求的是只要到达最后一行即可，因此我们的目标是找到最后一行中的最小值。这可以通过遍历最后一行并比较各个位置的值来实现。
- 最终返回的是这个最小值，而不是 dp[m][n] 的值，因为 dp[m][n] 只表示到达特定位置 [m, n] 的最小路径和，而题目要求的是到达最后一行任意位置的最小路径和。

3.代码编写

class Solution 
{
public:
    int minFallingPathSum(vector<vector<int>>& matrix) 
    {
        int n = matrix.size();
        vector<vector<int>> dp(n + 1, vector<int>(n + 2, INT_MAX));
        for(int j = 0; j < n + 2; j++) dp[0][j] = 0;
        for(int i = 1; i <= n; i++)
        {
            for(int j = 1; j <= n; j++)
            {
                dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i - 1][j + 1])) + matrix[i - 1][j - 1];
            }
        }
        int ret = INT_MAX;
        for(int i = 1; i <= n; i++) ret = min(ret, dp[n][i]);
        return ret;
    }
};