一、队列

1.概念

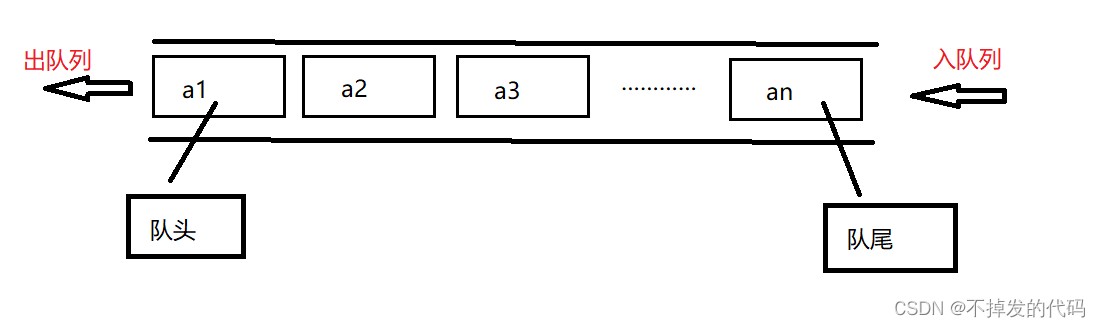
队列：是允许在一端进行插入操作，而在另一端进行删除操作的线性表。

队列是一种先进先出的（First In First Out）的线性表，简称FIFO。允许插入的一端称为队尾，允许删除的一端称为对头。

假设队列是queue = （a1,a2,a3,……,an），那么a1就是对头元素，而an是队尾元素。

2.队列的使用

队列在Java底层中是通过链表来实现的
队列中最常用的方法为：

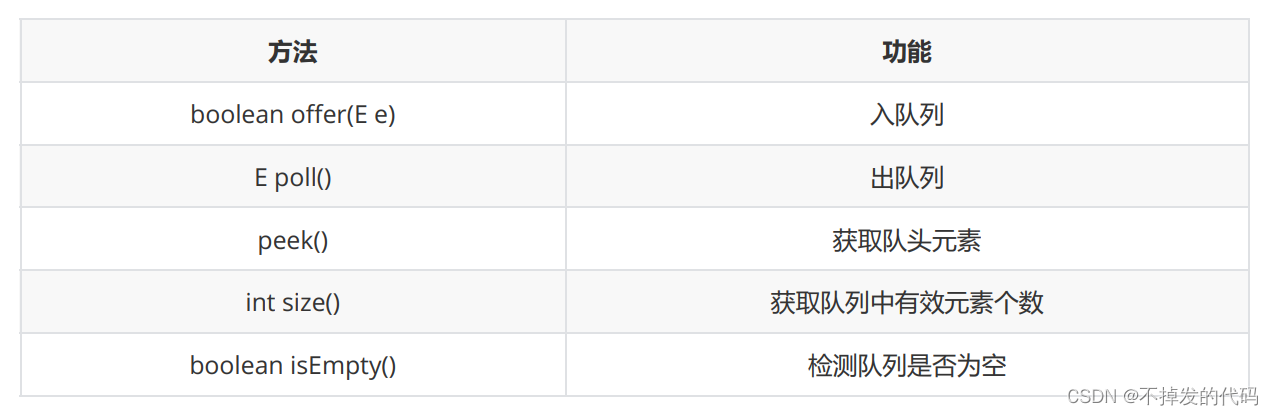
3.队列的模拟实现

队列在Java底层中肯定要保证右足够的存储空间，所以在实现是采用链表来实现。

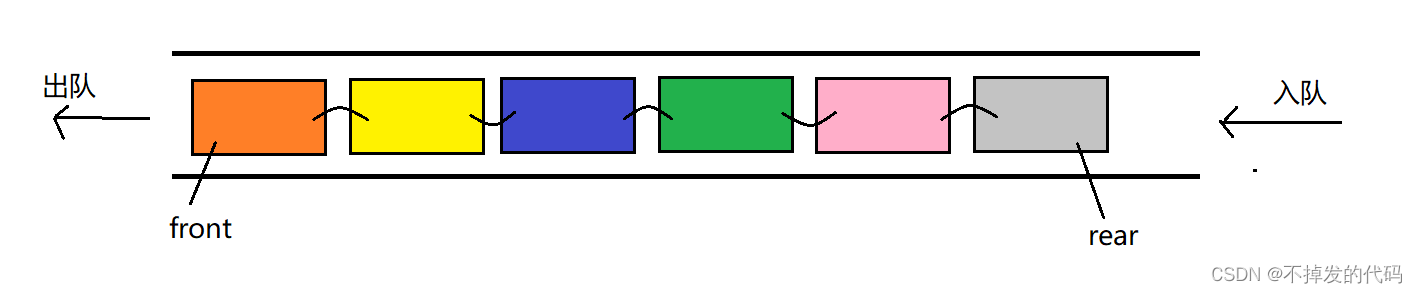
我们可以在队头进行元素的删除，在队尾进行元素的添加。

public class Queue {
    private static class Node {
        int val;
        Node next;

        public Node(int val) {
            this.val = val;
        }
    }

    private Node front;
    private Node rear;

    public Queue() {
    }

    public int offer (int val) {
        Node node = new Node(val);
        if (front == null) {
            front = node;
            rear = node;
            return val;
        }
        rear.next = node;
        rear = node;
        return val;
    }

    public int poll () {
        int top = front.val;
        if (isEmpty()) {
            throw new RuntimeException("the queue is empty ! ");
        }
        front = front.next;
        return top;
    }

    public boolean isEmpty() {
        return front == null;
    }

    public int peek () {
        if (isEmpty()) {
            throw new RuntimeException("the queue is empty ! ");
        }
        return front.val;
    }

    public int size () {
        Node temp = front;
        int size = 0;
        while (temp != null) {
            size++;
            temp = temp.next;
        }
        return size;
    }
}

二、循环队列

1.基本概念

上面实现的队列不难知道当出队列时front往后移，并且这个过程是不可逆的，如果是有大量的数据的时候，很容易造成内存的空间的随意使用。

为了解决上述问题，我们就提出了循环队列，所以解决溢出的问题就是后面满了，就再从头开始，也就是头尾相接的循环。

我们把这种队列头尾相接的顺序存储结构称为循环队列。

• 红色字体：数组下标
• 蓝色字体：数据域
• 黑色字体：队头队尾

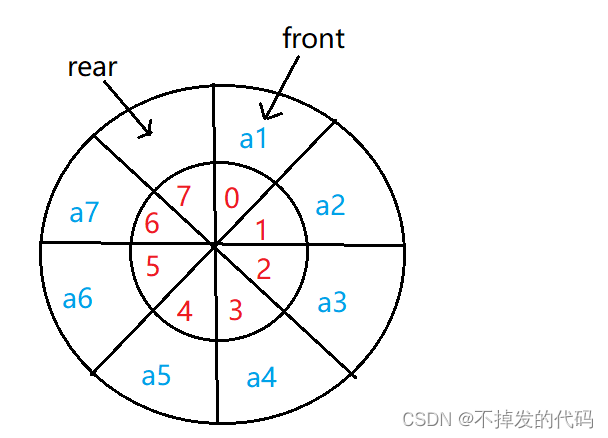
要达到循环的效果我们就必须浪费掉一个存储空间，要是不舍弃这个存储空间则判断队列满与队列空的时候就矛盾了。

2.代码实现

public class CircularQueue {
    private int front;
    private int rear;
    private int[] circle;

    public CircularQueue(int k) {
        //浪费掉一个存储空间
        circle = new int[k+1];
    }

	//入队列
    public boolean enQueue(int value) {
        if (isFull()) {
            return false;
        }
        circle[rear] = value;
        //因为是循环队列，不能写++，要以取模的方式
        rear = (rear + 1) % circle.length;
        return true;
    }
	
	//出队列
    public boolean deQueue() {
        if (isEmpty()) {
            return false;
        }
        front = (front + 1) % circle.length;
        return true;
    }
	
	//返回队头元素
    public int Front() {
        if (isEmpty()) {
            return -1;
        }
        return circle[front];
    }

	//返回队尾元素
    public int Rear() {
        if (isEmpty()) {
            return -1;
        }
        return circle[(rear - 1 + circle.length) % circle.length];
    }

    public boolean isEmpty() {
        return rear == front;
    }

    public boolean isFull() {
        return ((rear + 1) % circle.length) == front;
    }

    
}