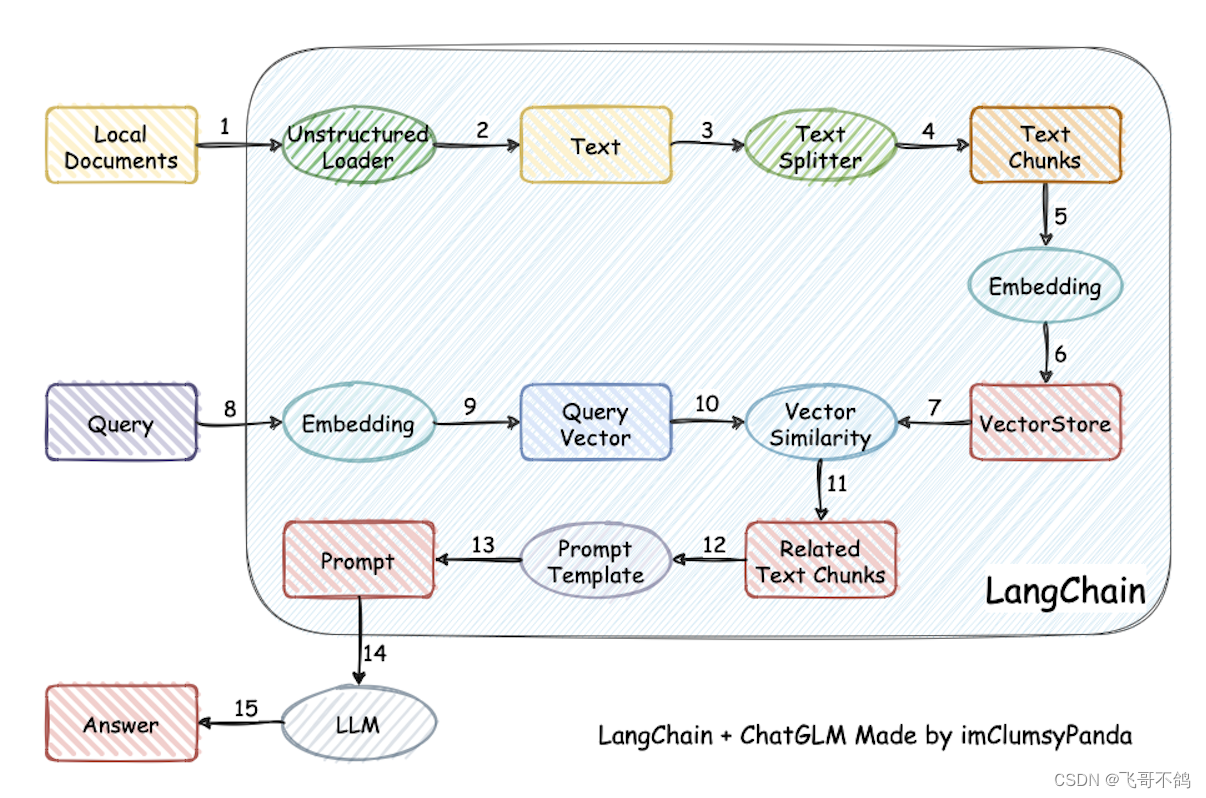
一、感知机
感知机接收多个输入信号,输出一个信号。这里所说的“信号”可以想象成电流或河流那样具备“流动性”的东西。 但是,和实际的电 流不同的是,感知机的信号只有“流 / 不流”( 1 / 0 )两种取值。在本书中, 0 对应“不传递信号”, 1 对应“传递信号”。
x
1
、
x
2
是输入信号,y
是输出信号,
w
1
、
w
2
是
权重(
w
是
weight
的首字母)。图中的○称为“神
经元”或者“节点”。输入信号被送往神经元时,会被分别乘以固定的权重
(
w
1
x
1
、
w
2
x
2
)。神经元会计算传送过来的信号的总和,只有当这个总和超过了某个界限值时(w1x1+w2x2>θ),才会输出1
。这也称为“神经元被激活”
。这里将这个界
限值称为
阈值
,用符号
θ
表示。
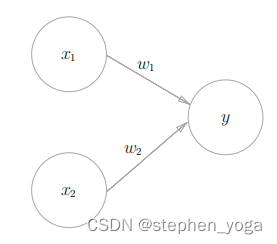
感知机的多个输入信号都有各自固有的权重,这些权重发挥着控制各个信号的重要性的作用。也就是说,权重越大,对应该权重的信号的重要性就
越高。
二、简单逻辑电路
1.与门
用感知机表示与门
(w1, w2, θ) = (0.5, 0.5, 0.7)
当且仅当,x1=1,x2=1时,w1x1+w2x2>θ,感知机输出1
注:参数选择有无数个,这里和下文只举例说明
2.与非门
用感知机表示与非门
(w1, w2, θ) = (−0.5, −0.5, −0.7)
当且仅当x1=1,x2=1时,w1x1+w2x2<θ,感知机输出0
3.或门
用感知机表示或门
(w1, w2, θ) = (0.5, 0.5, 0.1)
当且仅当x1=0,x2=0时,w1x1+w2x2<θ,感知机输出0
三、感知机的实现
1.简单的实现
def AND(x1,x2):
w1,w2,theta=0.5,0.5,0.7
tmp=x1*w1+x2*w2
if tmp<=theta:
return 0
elif tmp>theta:
return 1
print(AND(0,0))
print(AND(1,0))
print(AND(0,1))
print(AND(1,1))
#输出分别为0 0 0 1 符合与门的真值表2.导入权重和偏置
将感知机的输出表达式改为b+w1x1+w2x2>0,其中b为偏置,w1w2为权重。
用Numpy实现上述功能
import numpy as np
x=np.array([0,1])#输入
w=np.array([0.5,0.5])#权重
b=-0.7
print(w*x)
print(np.sum(w*x))
print(np.sum(w*x)+b)
#结果为
#[0. 0.5]
#0.5
#-0.199999999999999963.使用权重和偏置的实现
#与门
import numpy as np
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
#与非门
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5]) # 仅权重和偏置与AND不同!
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
#或门
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5]) # 仅权重和偏置与AND不同!
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1w 1 和 w 2 是控制输入信号的重要性的参数,而偏置是调整神经元被激活的容易程度(输出信号为 1 的程度)的参数。比如,若 b 为 − 0 . 1 ,则只要输入信号的加权总和超过 0 . 1 ,神经元就会被激活。但是如果 b 为 − 20 . 0 ,则输入信号的加权总和必须超过 20 . 0 ,神经元才会被激活。
四、感知机的局限性
1.异或门
异或门的真值表中,当且仅当x1x2不同时,才会输出1.
异或门不能用上述的感知机实现,具体分析如下
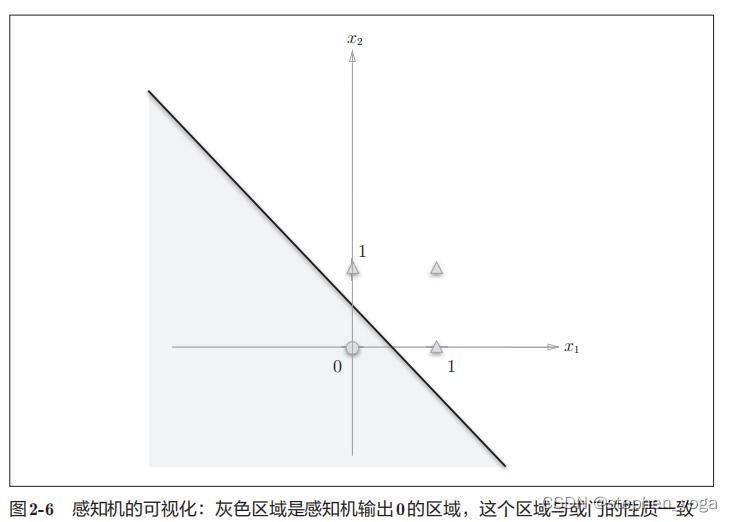
上图是或门的情况,由直线−0.5 + x1 + x2 = 0分割开的两个空间(实际上就是直线y=-x+0.5的图像,参考书中是前面这样写的)。其中一个空间输出1,另一个空间输出0.从图中可以看出用一条直线可以分开○和△(○表示感知机输出为0,△表示感知机输出为1)
我们再看异或门的情况
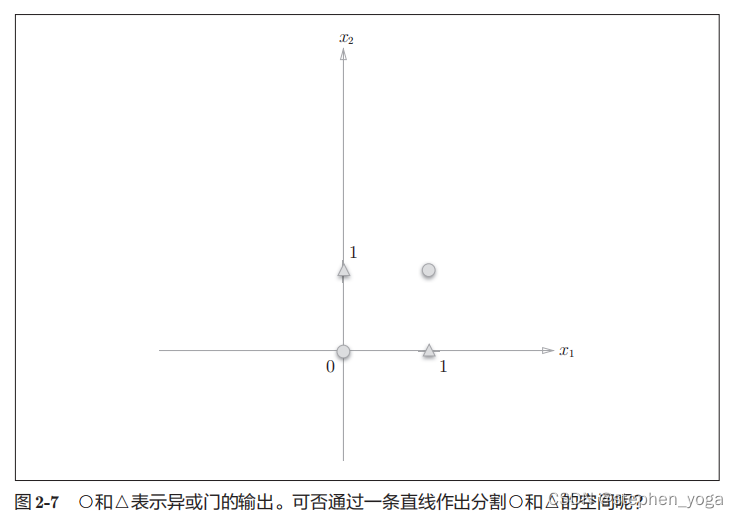
很显然用一条直线是不能区分开的
2.线性和非线性
上面讨论到用直线无法区分两个区域,考虑用曲线进行分割
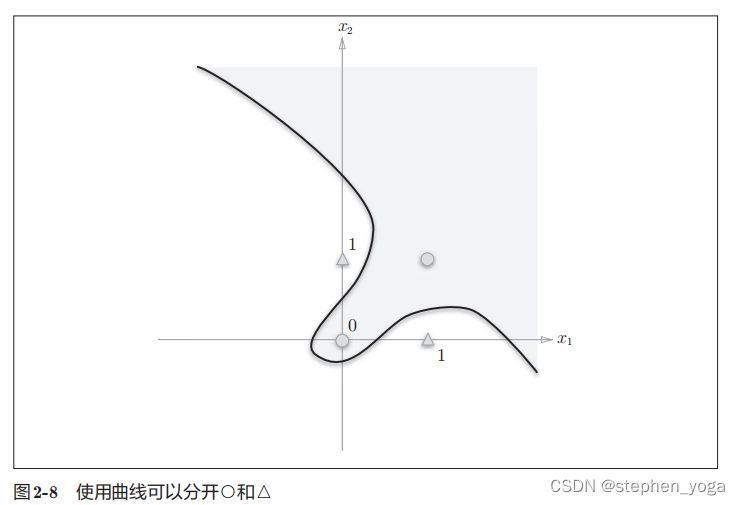
这样的曲线分割而成的空间称为非线性
空间,由直线分割而成的空间称为
线性
空间。
五、多层感知机
1.已有门电路的组合
通过与门、或门、与非门的组合可以实现异或门
讲到的感知机的局限性,严格地讲,应该是“单层感知机无法表示异或门”或者“单层感知机无法分离非线性空间”。接下来,我 们将看到通过组合感知机(叠加层)就可以实现异或门。
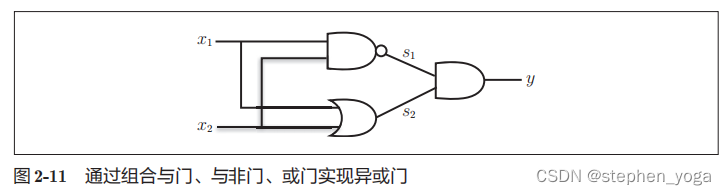
(这个组合我是试出来的,不知道有没有什么组合的原理,书中也没讲)
2.异或门的实现
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
def XOR(x1, x2):
s1=NAND(x1,x2)
s2=OR(x1,x2)
y=AND(s1,s2)
return y
print(XOR(0,0))
print(XOR(1,0))
print(XOR(0,1))
print(XOR(1,1))
#输出为0 1 1 0 符合异或门的真值表异或门是一种多层结构的神经网络。这里,将最左边的一列称为第 0 层,中间的一列称为第 1 层,最右边的一列称为第 2 层。实际上,与门、或门是单层感知机,而异或门是 2 层感知机。叠加了多层的感知机也称为 多层感知机
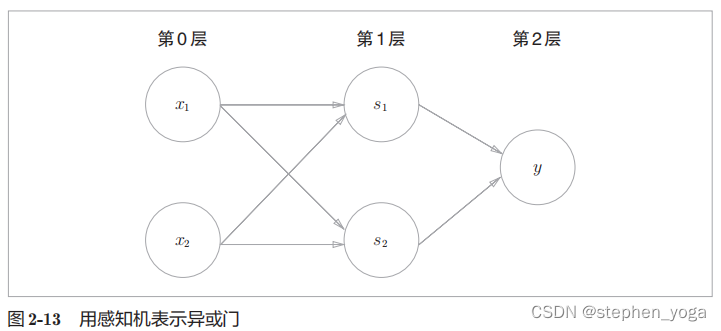
在图 2-13 所示的 2 层感知机中,先在第 0 层和第 1 层的神经元之间进行信号的传送和接收,然后在第 1 层和第 2 层之间进行信号的传送和接收,具体如下所示。1. 第 0 层的两个神经元接收输入信号,并将信号发送至第 1 层的神经元。2. 第 1 层的神经元将信号发送至第 2 层的神经元,第 2 层的神经元输出 y 。