目标
在本教程中,您将学习如何:
- 使用 OpenCV 函数 pyrUp()和 pyrDown()对给定图像进行下采样或上采样。
理论
注意
下面的解释属于 Bradski 和 Kaehler 的 Learning OpenCV 一书。
- 通常,我们需要将图像转换为与原始图像不同的大小。为此,有两种可能的选择:
- 放大图像(放大)或
- 缩小它(缩小)。
- 尽管 OpenCV 中有一个几何变换函数,可以从字面上调整图像大小(调整大小,我们将在以后的教程中展示),但在本节中,我们首先分析了图像金字塔的使用,它广泛应用于广泛的视觉应用。
图像金字塔
- 图像金字塔是图像的集合 - 所有图像都来自单个原始图像 - 这些图像被连续下采样,直到达到某个所需的停止点。
- 图像金字塔有两种常见的类型:
- 高斯金字塔:用于对图像进行缩减采样
- 拉普拉斯金字塔:用于从金字塔下部的图像(分辨率较低)重建上采样图像
- 在本教程中,我们将使用高斯金字塔。
高斯金字塔
- 将金字塔想象成一组层,其中层越高,尺寸越小。
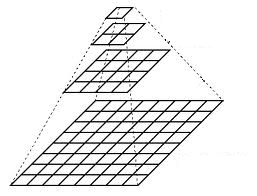
- 每一层都从下到上编号,因此层(i+1)(表示为 G_(i+1)小于层I(Gi)。
-
为了在高斯金字塔中生成层(I+1)我们执行以下操作:
- 用高斯核卷积Gi:
-

- 删除每个偶数行和列。
- 您可以很容易地注意到,生成的图像将恰好是其前身的四分之一。在输入图像 \(G_{0}\)(原始图像)上迭代此过程将生成整个金字塔。
- 上述过程对于图像的缩减采样非常有用。如果我们想让它变大怎么办?:用零填充的列 ( \(0 \))
- 首先,将图像在每个维度上放大到原始图像的两倍,使用新的偶数行和
- 使用上面显示的相同内核(乘以 4)执行卷积,以近似“缺失像素”的值
- 这两个过程(如上所述的下采样和上采样)由 OpenCV 函数 pyrUp() 和 pyrDown() 实现,我们将在下面代码的示例中看到:
注意
当我们减小图像的大小时,我们实际上丢失了图像的信息。
演示代码:
C++
本教程代码如下所示。
您也可以从这里下载
#include "iostream"
#include "opencv2/imgproc.hpp"
#include "opencv2/imgcodecs.hpp"
#include "opencv2/highgui.hpp"
using namespace std;
using namespace cv;
const char* window_name = "Pyramids Demo";
int main( int argc, char** argv )
{
cout << "\n Zoom In-Out demo \n "
"------------------ \n"
" * [i] -> Zoom in \n"
" * [o] -> Zoom out \n"
" * [ESC] -> Close program \n" << endl;
const char* filename = argc >=2 ? argv[1] : "chicky_512.png";
// Loads an image
Mat src = imread( samples::findFile( filename ) );
// Check if image is loaded fine
if(src.empty()){
printf(" Error opening image\n");
printf(" Program Arguments: [image_name -- default chicky_512.png] \n");
return EXIT_FAILURE;
}
for(;;)
{
imshow( window_name, src );
char c = (char)waitKey(0);
if( c == 27 )
{ break; }
else if( c == 'i' )
{ pyrUp( src, src, Size( src.cols*2, src.rows*2 ) );
printf( "** Zoom In: Image x 2 \n" );
}
else if( c == 'o' )
{ pyrDown( src, src, Size( src.cols/2, src.rows/2 ) );
printf( "** Zoom Out: Image / 2 \n" );
}
}
return EXIT_SUCCESS;
}解释
C++
让我们检查一下程序的一般结构:
加载图像
const char* filename = argc >=2 ? argv[1] : "chicky_512.png";
// Loads an image
Mat src = imread( samples::findFile( filename ) );
// Check if image is loaded fine
if(src.empty()){
printf(" Error opening image\n");
printf(" Program Arguments: [image_name -- default chicky_512.png] \n");
return EXIT_FAILURE;
}创建窗口
imshow( window_name, src );消息循环:
for(;;)
{
imshow( window_name, src );
char c = (char)waitKey(0);
if( c == 27 )
{ break; }
else if( c == 'i' )
{ pyrUp( src, src, Size( src.cols*2, src.rows*2 ) );
printf( "** Zoom In: Image x 2 \n" );
}
else if( c == 'o' )
{ pyrDown( src, src, Size( src.cols/2, src.rows/2 ) );
printf( "** Zoom Out: Image / 2 \n" );
}
}执行无限循环,等待用户输入。如果用户按 ESC,我们的程序将退出。此外,它有两个选项:
-
执行上采样 - 缩放 'i'n(按下“i”后)
我们使用带有三个参数的函数 pyrUp():
- src:当前和目标图像(显示在屏幕上,应该是输入图像的双倍)
- Size( tmp.cols*2, tmp.rows*2 ) :目标大小。由于我们是上采样,pyrUp() 的大小是输入图像的两倍(在本例中为 src)。
else if( c == 'i' )
{ pyrUp( src, src, Size( src.cols*2, src.rows*2 ) );
printf( "** Zoom In: Image x 2 \n" );
}-
执行缩减采样 - 缩放 'o'ut(按下 'o' 后)
我们使用带有三个参数的函数 pyrDown() (类似于 pyrUp()):
- src:当前和目标图像(显示在屏幕上,应该是输入图像的一半)
- Size(tmp.cols/2, tmp.rows/2 ) :目标大小。由于我们正在缩减采样,pyrDown() 需要输入图像的一半大小(在本例中为 src)。
else if( c == 'o' )
{ pyrDown( src, src, Size( src.cols/2, src.rows/2 ) );
printf( "** Zoom Out: Image / 2 \n" );
}请注意,输入图像可以除以 2 倍(在两个维度上)非常重要。否则,将显示错误。
结果
- 默认情况下,
samples/data程序调用文件夹中的图像chicky_512.png。请注意,此图像是 \(512 \times 512\),因此下采样不会生成任何错误 ( \(512 = 2^{9}\))。原图如下图所示:

- 首先,我们通过按“d”来应用两个连续的 pyrDown()操作。我们的输出是:

- 注意,由于我们正在减小图像的大小,我们应该会失去一些分辨率。在我们应用 pyrUp() 两次(按“u”)后,这一点很明显。我们现在的输出是:

参考文献:
1、《Image Pyramids》-----Ana Huamán