一、背景
双调欧几里得旅行商问题(Double Bitonic TSP)是欧几里得旅行商问题(Euclidean TSP)的一个特殊版本。在标准的欧几里得旅行商问题中,我们需要找到一条最短的路径,这条路径要求访问者从一个城市出发,经过所有其他城市恰好一次,最后返回到起始城市。这个问题是非常复杂的,尤其是当城市数量很多时,可能的路径组合数量是巨大的,因此很难快速找到一个最优解。
而双调欧几里得旅行商问题对路径的走法做了特殊的限制,使得问题变得更加简单。在双调版本中,旅行商不是要访问所有的城市并返回起点,而是只需要从最左边的城市出发,沿着一条向右的路径经过一些城市,到达最右边,然后沿着一条向左的路径返回起点。简单来说,就像是先向右走一段,到达某个点后立即掉头向左走,形成一个类似“V”字型的路径。
这个版本的旅行商问题的特点是路径分为两个部分:向右的部分(递增部分)和向左的部分(递减部分)。这种特殊的走法限制了旅行商的行动,使得问题可以通过更加高效的算法来解决,比如动态规划,而不需要像解决标准欧几里得旅行商问题那样进行复杂的计算。
在解决双调欧几里得旅行商问题(Double Bitonic TSP)时,我们的目标是找到一条从最左边的点开始,严格向右前进至最右边的点,然后严格向左返回起始点的最短路径。这个问题的一个关键特点是,路径的第一部分是递增的(向右),第二部分是递减的(向左)。这种特殊的路径要求使得问题可以通过一种相对简单的动态规划方法来解决,其时间复杂度为O(n²)。
二、问题描述
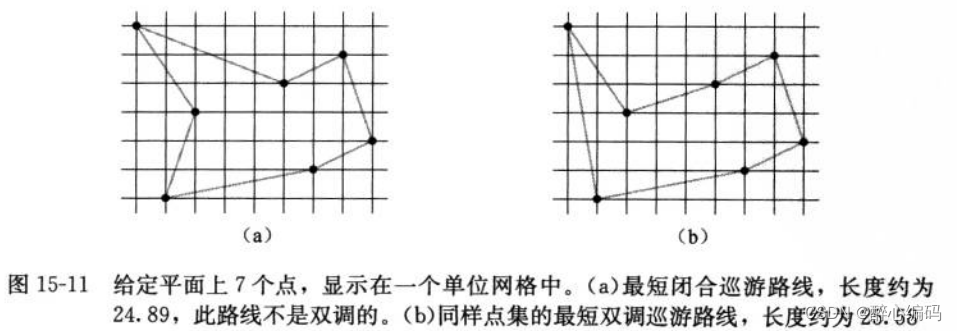
给定平面上的n个点,每个点具有唯一的x坐标和y坐标。我们需要找到一条从最左边的点开始,严格向右到达最右边的点,然后严格向左返回起始点的最短路径。这条路径被称为双调巡游路线。
三、算法设计
3.1 动态规划方法
-
初始化:创建两个数组
rightMin和leftMin,它们的长度都为n,用于存储从左到右和从右到左的最小累积距离。 -
向右扫描:遍历点集,计算到达每个点的最短路径。对于每个点i,我们从
rightMin[i-1]开始,加上从点i-1到点i的距离,然后更新rightMin[i]。 -
向左扫描:从最右边的点开始,逆向遍历点集,计算到达每个点的最短路径。对于每个点i,我们从
leftMin[i+1]开始,加上从点i+1到点i的距离,然后更新leftMin[i]。 -
计算总距离:对于每个点i,计算
rightMin[i] + leftMin[i+1]的值,这代表了从最左边的点开始,经过点i,然后返回起始点的最短路径。我们需要找到这些值中的最小值,这就是我们要找的双调巡游路线的总距离。 -
重构路径:一旦我们找到了最短路径的总距离,我们可以通过回溯
rightMin和leftMin数组来重构实际的路径。
3.2 伪代码
function DoubleBitonicTSP(points):
n = length(points)
rightMin = new array of size n
leftMin = new array of size n
totalDistance = infinity
// 初始化
for i from 1 to n:
rightMin[i] = 0
leftMin[i] = 0
// 向右扫描
for i from 1 to n-1:
for j from i to n-1:
rightMin[j] = min(rightMin[j], rightMin[j-1] + distance(points[j], points[j-1]))
// 向左扫描
for i from n-1 down to 1:
for j from i to 1:
leftMin[j] = min(leftMin[j], leftMin[j+1] + distance(points[j], points[j+1]))
// 计算总距离
for i from 1 to n-1:
totalDistance = min(totalDistance, rightMin[i] + leftMin[i+1])
// 重构路径
path = reconstructPath(rightMin, leftMin, totalDistance)
return path, totalDistance
3.3 C代码实现
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
typedef struct {
double x;
double y;
} Point;
double distance(const Point& a, const Point& b) {
return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2));
}
void doubleBitonicTSP(Point points[], int n, double* totalDistance, Point* path) {
double* rightMin = (double*)malloc(n * sizeof(double));
double* leftMin = (double*)malloc(n * sizeof(double));
for (int i = 0; i < n; i++) {
rightMin[i] = 0;
leftMin[i] = 0;
}
// 向右扫描
for (int i = 1; i < n; i++) {
double minDist = rightMin[i - 1];
for (int j = i; j < n; j++) {
rightMin[j] = min(minDist, rightMin[j - 1] + distance(points[j], points[j - 1]));
minDist = rightMin[j];
}
}
// 向左扫描
for (int i = n - 2; i >= 0; i--) {
double minDist = leftMin[i + 1];
for (int j = i; j < n - 1; j++) {
leftMin[j] = min(minDist, leftMin[j + 1] + distance(points[j], points[j + 1]));
minDist = leftMin[j];
}
}
*totalDistance = infinity;
for (int i = 0; i < n - 1; i++) {
*totalDistance = fmin(*totalDistance, rightMin[i] + leftMin[i + 1]);
}
// 重构路径
// ... (此处省略重构路径的代码)
free(rightMin);
free(leftMin);
}
int main() {
// 示例:给定点集
Point points[] = {{0, 0}, {1, 1}, {2, 2}, {3, 3}, {4, 4}, {5, 5}, {6, 6}};
int n = sizeof(points) / sizeof(points[0]);
double totalDistance;
Point path[2 * n - 1]; // 路径长度为2n - 1
doubleBitonicTSP(points, n, &totalDistance, path);
// 输出结果
printf("Total Distance: %f\n", totalDistance);
// 输出路径
for (int i = 0; i < 2 * n - 1; i++) {
printf("(%f, %f) ", path[i].x, path[i].y);
}
printf("\n");
return 0;
}
3.4 算法分析
时间复杂度:算法的两个主要部分是向右扫描和向左扫描,每个部分都包含一个嵌套循环,它们的时间复杂度都是O(n²)。因此,整个算法的时间复杂度是O(n²)。
空间复杂度:我们使用了两个数组rightMin和leftMin,每个数组的大小为n,因此空间复杂度为O(n)。
四、 结论
通过上述算法,我们可以在多项式时间内解决双调欧几里得旅行商问题。这个问题的简化版本通过限制路径的性质,使得原本NP难的旅行商问题变得可解。这种简化在实际应用中非常有用,尤其是在需要快速得到一个近似最优解的情况下。通过动态规划的方法,我们可以有效地找到最短的双调巡游路线,并且可以通过重构算法来确定实际的路径。这种方法不仅适用于理论研究,也适用于实际问题,如物流规划、电路设计等领域。