基于R语言实现的负二项回归模型【理解与实现】-理解负二项回归模型和泊松回归模型之间的区别

news2024/11/17 13:51:45

前言

我们可以在R语言中使用MASS包中的glm.nb函数来拟合负二项模型，以及使用glm函数来拟合泊松模型。以下是一个详细的过程，包括模拟数据的生成、模型的拟合、结果的比较和解释。

需要的包

if (!require("MASS")) install.packages("MASS")
if (!require("ggplot2")) install.packages("ggplot2")

library(MASS)
library(ggplot2)

产生模拟数据

生成具有过度离散特性的计数数据。

set.seed(123)  # 设置随机数种子

# 创建一些预测变量
n <- 1000
x1 <- rnorm(n)
x2 <- rnorm(n)

# 创建过度离散数据
mu <- exp(1 + 0.3*x1 - 0.4*x2)  # 真实均值
size <- 1.5  # 负二项分布的大小参数，控制离散程度
k <- rnbinom(n, mu = mu, size = size)

data <- data.frame(counts=k, x1=x1, x2=x2)

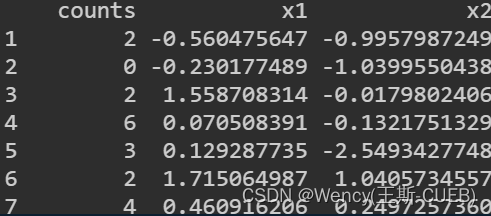
在这里插入图片描述

拟合泊松模型

使用glm函数以泊松分布拟合数据。

poisson_model <- glm(counts ~ x1 + x2, family = poisson, data = data)
summary(poisson_model)

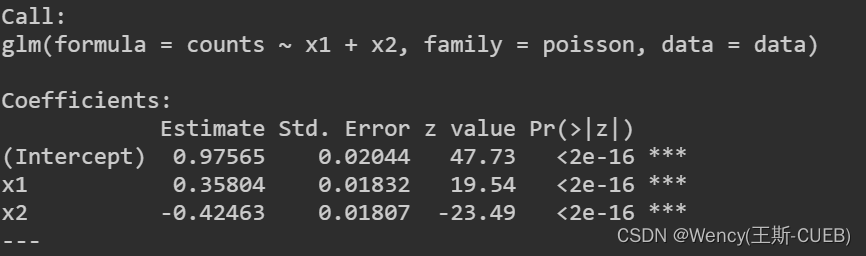
在这里插入图片描述

拟合负二项模型

使用glm.nb函数以负二项分布拟合同样的数据。

negbin_model <- glm.nb(counts ~ x1 + x2, data = data)
summary(negbin_model)

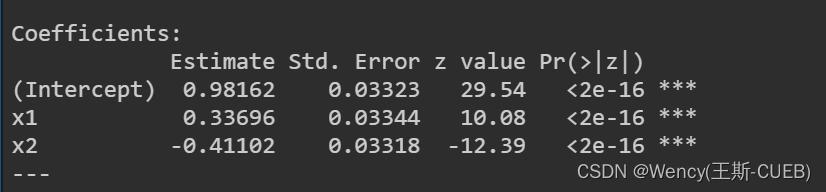
在这里插入图片描述

结果的比较和诊断

比较两个模型的拟合优度，检查是否有过度离散。

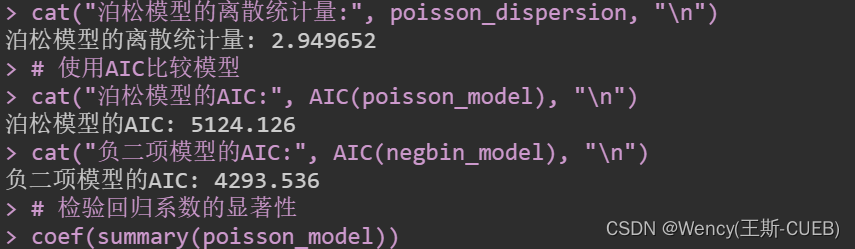
# 计算泊松模型的离散统计量
poisson_dispersion <- sum(residuals(poisson_model, type = "pearson")^2) / poisson_model$df.residual
cat("泊松模型的离散统计量:", poisson_dispersion, "\n")

# 使用AIC比较模型
cat("泊松模型的AIC:", AIC(poisson_model), "\n")
cat("负二项模型的AIC:", AIC(negbin_model), "\n")

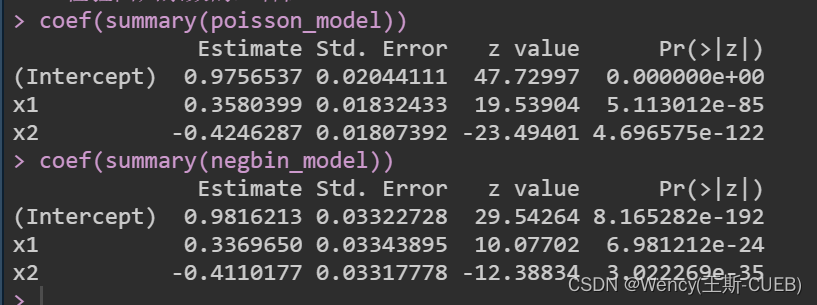
# 检验回归系数的显著性
coef(summary(poisson_model))
coef(summary(negbin_model))

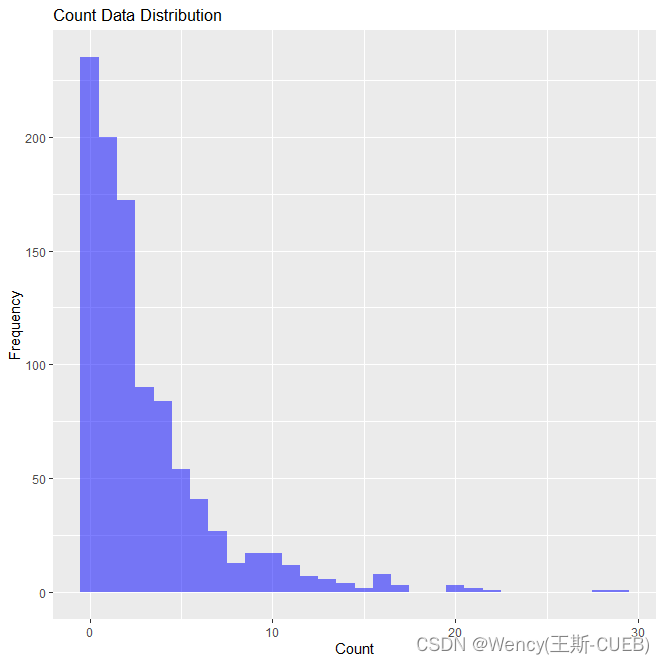
# 可视化
ggplot(data, aes(x = counts)) +
  geom_histogram(binwidth = 1, fill = "blue", alpha = 0.5) +
  labs(title = "Count Data Distribution", x = "Count", y = "Frequency")

在这里插入图片描述

解释

离散统计量：泊松模型的离散统计量应接近1。如果这个值显著大于1，就说明有过度离散。
AIC（赤池信息量准则）：AIC提供了一个衡量模型拟合优度的方法，考虑到了模型复杂性。更小的AIC值通常意味着更好的模型。
回归系数：对于两个模型，我们都可以查看回归系数的估计和它们的统计显著性。
可视化：生成数据的直方图可以帮助我们直观了解数据的分布。对于过度离散的数据，我们预期直方图会显示出尾部较重或者集中在0的频数较多。
通过这个过程，我们可以清楚地看到负二项模型和泊松模型在处理过度离散数据时的不同表现。实际上，负二项模型更适合这些数据，因为它考虑到了变异性，并且AIC值也应该较低，表明更好的数据拟合。通过查看系数和它们的显著性，我们可以确定哪个模型提供了更可信的解释。

在这里插入图片描述