【NOI】C++程序设计入门五

文章目录

前言
一、两数交换
- 1.概念
- 2.样例
- 3.交换方法
- - 3.1 方法一：请个临时工
  - 3.2 方法二：加法交换律
  - 3.3 方法三：swap函数
- 4.小结
二、拆位求解
- 1.概念
- 2.用法
三、样题讲解
- 问题：1605. 求一个两位数的个位和十位的和
- 问题：1606. 求一个两位数倒序的结果
- 问题：1027 - 求任意三位数各个数位上数字的和
- 问题：1028 - 输入一个三位数，把个位和百位对调后输出
- 问题：1390-请从键盘读入一个四位整数，求这个四位整数各个位的和是多少？
- 问题：1109 - 加密四位数
四、总结
五、感谢

前言

在先前的学习历程中，我们已深入探讨了变量与数据类型的概念，并对其中的核心成员——整型int、浮点型float与double进行了细致研究。通过大量的实践练习，我们已熟练掌握了涉及整数与小数的基本运算技巧。这一节中，我们将目光转向程序设计中应用广泛且颇具实用价值的两个主题：变量交换与拆位求解。

本节内容将系统地介绍变量交换的几种常见方法，包括借助临时变量、利用加法交换律以及使用C++内置的swap函数，同时通过实例演示如何运用这些方法实现变量值的有效互换。接下来，我们将探讨拆位求解的基本原理，阐述如何通过取模和除法运算来获取一个数的各个数位，并结合样题详细展示如何将这些知识应用于实际问题的解决。

学习路线：C++从入门到NOI学习路线

学习大纲：C++全国青少年信息学奥林匹克竞赛（NOI）入门级-大纲

一、两数交换

1.概念

首先，让我们来探讨什么是变量的交换以及为什么需要进行交换。变量交换，简而言之，就是两个或多个变量之间值的互换。

这种操作在多种情况下都非常有用。例如，当我们需要比较两个数的大小并交换它们的位置时，变量交换就显得尤为重要。通过交换，我们可以确保较大的数存储在变量A中，较小的数存储在变量B中，这对于后续的排序、查找或其他算法操作非常有帮助。

此外，在编写复杂的算法或数据结构时，变量交换也常用于临时存储数据或改变数据的顺序。比如，在实现链表反转、数组轮转等操作时，我们需要通过交换节点或元素的值来达到目的。

因此，对于NOI的学生来说，熟练掌握变量交换的技巧是非常必要的。

2.样例

老规矩，我们还是举例说明。

在这里插入图片描述

具体而言，假设我们有两个变量A和B，分别存储数值a和b，交换操作后，A应持有原属B的值b，而B则应持有原属A的值a。例如：

// 原始状态
int a = 10;
int b = 20;

// 变量交换后
a = 20; // 现在A持有原属B的值
b = 10; // 玎在B持有原属A的值

问题来了，那怎么样进行变量交换呢？

有人可能会想既然是交换两个数，那么直接a=b，b=a不就可以了吗。简单，下一题。

在这里插入图片描述

真的是这样吗？

废话不说，上代码！

在这里插入图片描述

怎么样，和设想的不一样吧？为什么呢？

哎，我们再来举个例子。

在这里插入图片描述

假如，小明和小刚两个人。小明有一个苹果🍎，小刚有一个香蕉🍌。他们两个人都想吃对方手里的水果，但是现在他们的一只手在做其他的事情，只有一只手拿着水果（反正只允许使用一只手）。这个时候他们能直接交换水果吗？

这样不就行了！( •̀ ω •́ )✧

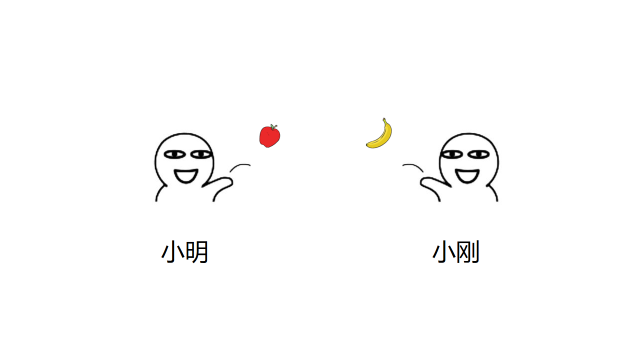
在这里插入图片描述

根本难不倒你，是吧！(╯▔皿▔)╯。

可以看到从现实生活出发也是办不到的，计算机会怎么处理我们刚才的程序呢？

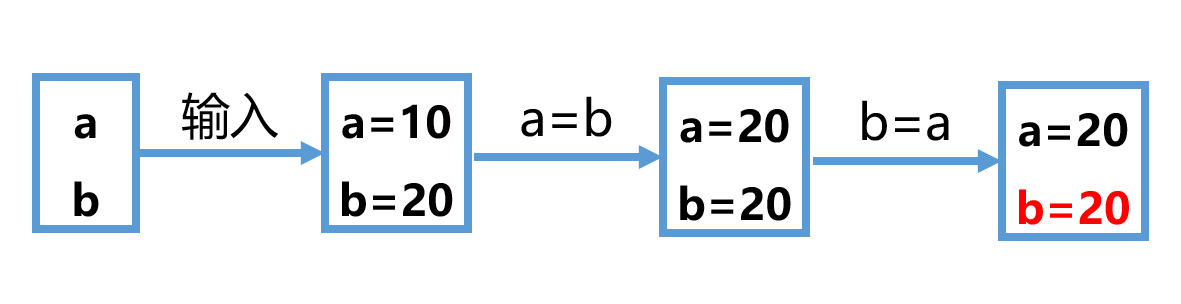
在这里插入图片描述

很显然，变量a，b就像是两个想要交换水果的小明，小刚。因为没有多的“手”，所以是无法进行交换的。

如果程序通过a=b，b=a的方式去交换两个数，可以看到当a=b时，a的值已经发生变化，不再是之前的值；所以在b=a时，b不能得到a=10这个原来的值。

3.交换方法

3.1 方法一：请个临时工

那应该怎么去交换呢？我想聪明的人肯定已经想到了，找个人帮忙啊。

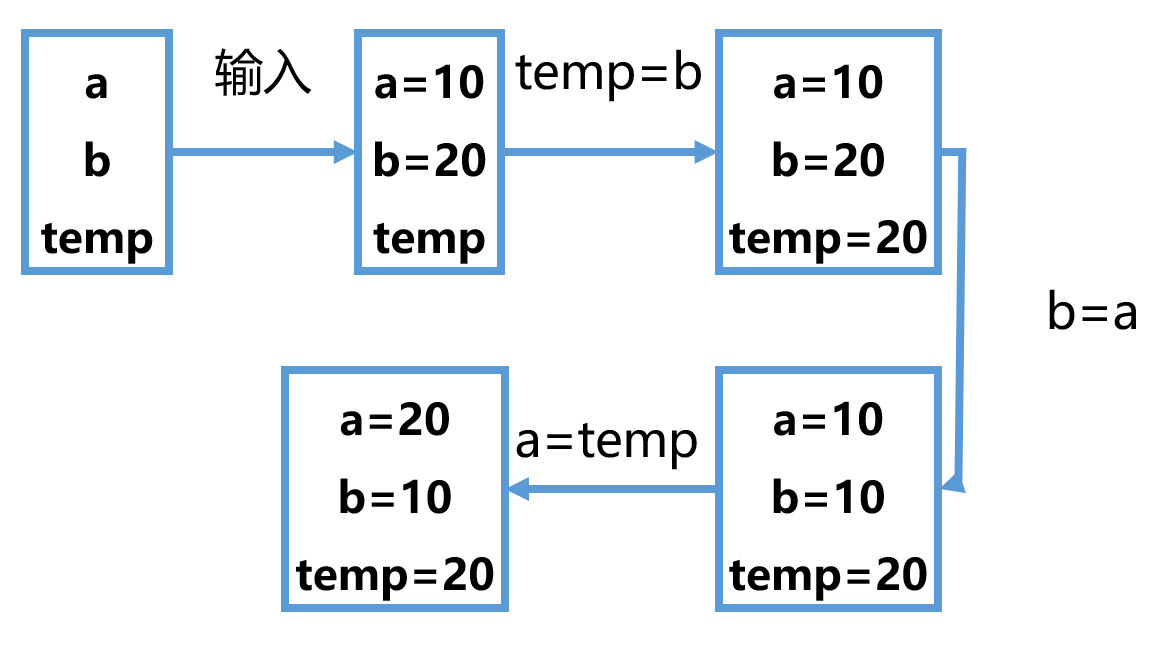
在这里插入图片描述

还是a=10，b=20。但是在b=a之前，我们通过temp=b这个操作，把b的值给了temp；然后当a需要b的值时，就去找temp要，如此就能实现两个数的交换。（temp 临时工）

在这里插入图片描述

程序如下：

#include<iostream>
using namespace std;
int main(){
	//1.分析问题： 已知：a，b的值。 未知：a，b交换以后的值。
	//2.定义变量 
	int a,b,temp;
	//3.输入数据
	cin>>a>>b;//a=10,b=20
	//4.数据计算
	temp=b;//temp=b=20
	b=a;//b=a=10
	a=temp;//a=temp=20
	//5.结果输出 
	cout<<a<<" "<<b;//20 10
}

有人可能会问了，那能不能不请临时工呢？

在这里插入图片描述

3.2 方法二：加法交换律

加法交换律:指两个加数相加,交换加数的位置,和不变。

假如a = 10，b = 20：

首先将a和b的和赋值给a。此时，a保存了原a和b的和。
接着，将新的a（即原a和b的和）减去原b，结果赋值给b。此时，b获得了原a的值。
最后，将新的a再次减去新的b（即原a），结果赋值给a。此时，a获得了原b的值。

经过以上三步计算，变量a和b的值成功互换。

在这里插入图片描述

程序如下：

#include<iostream>
using namespace std;
int main(){
	//1.分析问题： 已知：a，b的值。 未知：a，b交换以后的值。
	//2.定义变量 
	int a,b;
	//3.输入数据
	cin>>a>>b;
	//4.数据计算
	a=a+b;
	b=a-b;
	a=a-b;
	//5.结果输出 
	cout<<a<<" "<<b;
}

3.3 方法三：swap函数

在C++中，swap函数用于交换两个变量的值。实际上就是方法一，但是不需要自己去写交换逻辑。

程序如下：

#include<iostream>
using namespace std;
int main(){
	//1.分析问题： 已知：a，b的值。 未知：a，b交换以后的值。
	//2.定义变量 
	int a,b;
	//3.输入数据
	cin>>a>>b;
	//4.数据计算
	swap(a,b);
	//5.结果输出 
	cout<<a<<" "<<b;
}

4.小结

上面的三种方法都可以完成变量的交换。

在实际编程中，推荐使用方法一（临时变量法）或方法三（swap函数法）进行变量交换，因为它们既直观又不易出错。

而方法二更多是锻炼逻辑思维能力，包括对变量作用的理解、流程控制意识、数学知识运用、问题抽象与转化能力以及异常情况考虑等方面。

二、拆位求解

1.概念

学习拆位求解，我们需要知道什么拆位，具体来说拆的是什么“位”？

这里实际上指的是数位。数位是指一个数中的每一位的数字。

以十进制为例，它有十个基本符号（0到9），基数为10。当我们要拆分一个十进制数时，会按照以下方式：

个位：表示数值中最右侧的数字，其权重为1，即这个位置上的数字表示多少个1。
十位：紧邻个位左侧的数字，其权重为10，即这个位置上的数字表示多少个10。
百位：再往左一位，其权重为10^2=100，表示多少个100。
依次类推……

在这里插入图片描述

举个例子，对于十进制数 x=123：

个位：最右侧的数字是 3，表示有 3 个 1。
十位：中间的数字是 2，表示有 2 个 10。
百位：最左侧的数字是 1，表示有 1 个 100。

将这些按权重相加得到原数：

x=1×100+2×10+3×1=100+20+3=123

ok，是不是很简单。那怎么去得到每个数位的数呢？

2.用法

这里我们复习一下数学中的除法。有一个数x = 123。

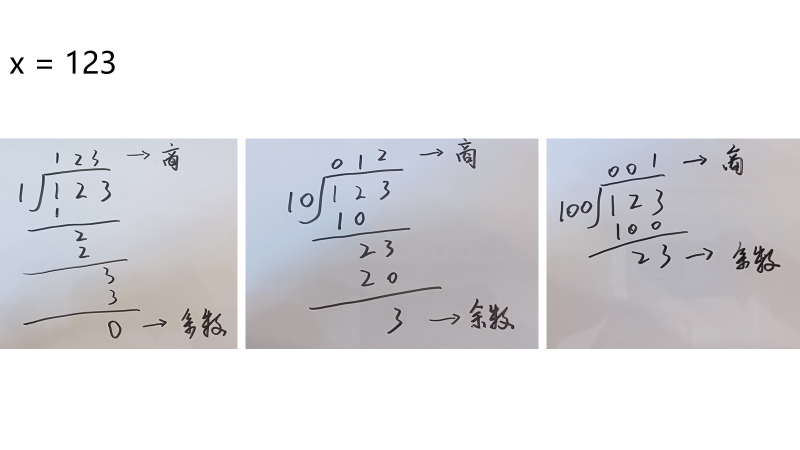
在这里插入图片描述
从第二张图可以看到，当123除以10以后产生了余数3，而3刚好是我们想要的个数位。那我们可以通过 %10 ( 取余 )得到3。

在这里插入图片描述

但是不能通过 %100 得到2，因为得到的数是23。如果这个数是12，那么 % 10 = 2。如何将123变成12呢？要知道int整数类型在除法时，是向下取正，不管余数是1还是9都不会进位。所以想得到12可以用123 / 10。

在这里插入图片描述

想要的得到最高位，直接除以最高位数的0即可。比如123想要得到1，那么直接123 / 100。

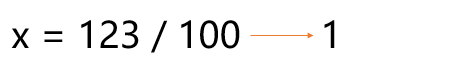
在这里插入图片描述

因此拆位的公式就是：

个位：%10；
中间位：/数位%10；
最高位：/数位。

三、样题讲解

问题：1605. 求一个两位数的个位和十位的和

类型：基本运算、拆位求解。

题目描述：

从键盘读入一个两位的整数 n ，请求出这个两位整数个位和十位的和是多少？

输入：

一个两位的整数 n 。

输出：

一个整数，代表 n 个位和十位的和。

样例：
输入：

输出：

在这里插入图片描述

1.分析问题

已知：一个两位的整数 n。
未知：这个两位整数个位和十位的和是多少？
关系：拆位求解。

2.定义变量

int n：用于存储输入的两位整数。
int sum：用于存储个位和十位数字之和。

	//二、数据定义 
	int n,sum;

3.输入数据

从标准输入（键盘）接收用户输入的两位整数，将其赋值给变量n。

	//三、数据输入 
	cin>>n;

4.数据计算

利用整数除法（/）和取模运算（%）进行拆位求解：

n / 10：整除运算，结果为n的十位数字（不带个位）。
n % 10：取模运算，结果为n除以10的余数，即n的个位数字。

	//四、数据计算 
	sum=n/10+n%10;

5.输出结果

将计算得到的sum值输出到标准输出（屏幕）。

	//五、输出结果 
	cout<<sum;

完整代码如下：

#include <bits/stdc++.h> 
using namespace std;

int main() {
    // 一、分析问题
    // 已知：一个两位的整数 n。
    // 未知：这个两位整数个位和十位的和是多少？
    // 关系：拆位求解

    // 二、数据定义
    // 定义变量 n 用于存储输入的两位整数
    // 定义变量 sum 用于存储个位和十位数字之和
    int n, sum;

    // 三、数据输入
    // 从标准输入（键盘）接收用户输入的两位整数，并将其赋值给变量 n
    cin >> n;

    // 四、数据计算
    // 利用整数除法（/）获取 n 的十位数字（不带个位）
    // 利用取模运算（%）获取 n 的个位数字
    // 将十位数字与个位数字相加，得到它们的和，并将结果赋值给变量 sum
    sum = n / 10 + n % 10;

    // 五、输出结果
    // 将计算得到的个位和十位数字之和（即变量 sum 的值）输出到标准输出（屏幕）
    cout << sum;

    // 六、程序结束
    // 添加 return 0; 语句，表示主函数正常结束并返回整数0
    return 0;
}

问题：1606. 求一个两位数倒序的结果

类型：基本运算、拆位求解

题目描述：

请输出一个两位的整数 n，倒过来的数，也就是输出这个两位数个位和十位颠倒的结果。
比如：整数 23 倒过来是 32，整数 18 倒过来是 81 ，整数 20 倒过来是 2。

输入：

两位整数 n。

输出：

n 倒过来的整数。

样例：

输入：

输出：

在这里插入图片描述

1.分析问题

已知：两位整数 n。
未知：n 倒过来的整数。
关系：拆位求解。

2.定义变量

int n：用于存储输入的两位整数。
int result：用于存储倒过来的整数。

	//二、数据定义 
	int n,result;

3.输入数据

从标准输入（键盘）接收用户输入的两位整数，将其赋值给变量n。

	//三、数据输入 
	cin>>n;

4.数据计算

利用整数除法（/）和取模运算（%）进行拆位求解：

利用整数除法（/）获取 n 的十位数字（不带个位），并乘以10得到其在新整数中的位置。
利用取模运算（%）获取 n 的个位数字。
将十位数字与个位数字相加，得到颠倒后的整数，并将结果赋值给变量 result。


    result = (n % 10) * 10 + (n / 10);

5.输出结果

将计算得到的倒过来的整数（即变量result的值）输出到标准输出（屏幕）。

	//五、输出结果 
	cout<<result;

完整代码如下：

#include <iostream>
using namespace std;

int main() {
    // 一、分析问题
    // 已知：一个两位的整数 n。
    // 未知：这个两位整数颠倒后的整数是多少？
    // 关系：拆位求解

    // 二、数据定义
    // 定义变量 n 用于存储输入的两位整数
    // 定义变量 result 用于存储颠倒后的整数
    int n, result;

    // 三、数据输入
    // 从标准输入（键盘）接收用户输入的两位整数，并将其赋值给变量 n
    cin >> n;

    // 四、数据计算
    // 利用整数除法（/）获取 n 的十位数字（不带个位），并乘以10得到其在新整数中的位置
    // 利用取模运算（%）获取 n 的个位数字
    // 将十位数字与个位数字相加，得到颠倒后的整数，并将结果赋值给变量 result
    result = (n % 10) * 10 + (n / 10);

    // 五、输出结果
    // 将计算得到的颠倒后的整数（即变量 result 的值）输出到标准输出（屏幕）
    cout << result;

    // 六、程序结束
    // 添加 return 0; 语句，表示主函数正常结束并返回整数0
    return 0;
}

问题：1027 - 求任意三位数各个数位上数字的和

类型：基础问题、拆位求解

题目描述：

对于一个任意的三位自然数 x ，编程计算其各个数位上的数字之和 S 。

输入：

输入一行，只有一个整数 x(100≤x≤999) 。

输出：

输出只有一行，包括 1 个整数。

样例：

输入：

输出：

在这里插入图片描述

1.分析问题

已知：x的值。
未知：x各数位相加后的和s。
关系：拆位求解

2.定义变量

定义了一个整型变量x用于存储输入的三位整数，定义了另一个整型变量s用于存储x各数位相加后的和。

	//2.定义变量 
	int x,s;

3.输入数据
通过cin从标准输入设备（通常是键盘）读取一个整数，并将其赋值给变量x。

	//3.输入数据 
	cin>>x;

4.数据计算

先通过取模运算得到x的个位数（ge），即int ge=x%10;
然后通过连续两次除以10并取模得到x的十位数（shi），即int
shi=x/10%10;
再通过除以100并向下取整得到x的百位数（bai），即int bai=x/100;
计算这三个数位上的数字之和并将结果赋值给变量s，即s=ge+shi+bai;

	//4.数据计算 
	int ge=x%10;
	int shi=x/10%10;
	int bai=x/100;

5.输出结果

使用cout将计算出的各数位之和（s）输出到标准输出设备（通常是显示器）。
返回0，表示程序正常结束。

	//5.输出数据
	cout<<s;

	return 0;

完整代码如下：

#include<iostream> // 引入C++标准输入输出流库，以便进行输入输出操作
using namespace std; // 使用标准命名空间std，简化代码中对库函数的调用

int main(){ // 程序主入口函数
    // 1. 分析问题：已知一个整数x，要求计算其各个数位上的数字之和。
    
    // 2. 定义变量 
    int x, s; // 定义整型变量x用于存储输入的三位整数，定义整型变量s用于存储各数位相加后的和
    
    // 3. 输入数据 
    cin>>x; // 从标准输入（如键盘）读取一个整数并将其赋值给变量x
    
    // 4. 数据计算 
    int ge = x % 10; // 计算x的个位数，通过取模运算获取
    int shi = x / 10 % 10; // 计算x的十位数，通过连续除以10并取模获取
    int bai = x / 100; // 计算x的百位数，直接除以100并向下取整获取
    
    s = ge + shi + bai; // 将各数位的数值相加求和，并将结果存入变量s
    
    // 5. 输出数据
    cout<<s; // 将计算得到的各数位之和输出到标准输出（如显示器）

    return 0; // 主函数返回0，表示程序正常结束
} // 结束main函数

问题：1028 - 输入一个三位数，把个位和百位对调后输出

类型：基础问题

题目描述：

输入一个三位自然数，然后把这个数的百位数与个位数对调，输出对调后的数。

输入：

输入一行，只有一个整数 x(100≤x≤999) 。

输出：

输出只有一行，包括 1 个整数。

样例：

输入：

输出：

输入：

输出：

在这里插入图片描述

1.分析问题

已知：x的值。
未知：对调后的数。
关系：拆位求解

2.定义变量

定义了一个整型变量x用于存储输入的三位整数。

	int x,g,s,b;

3.输入数据

通过cin从标准输入设备（通常是键盘）读取一个整数，并将其赋值给变量x。

	cin>>x;

4.数据计算

先通过取模运算得到x的个位数（ge），即int ge=x%10;
然后通过连续两次除以10并取模得到x的十位数（shi），即int shi=x/10%10;
再通过除以100并向下取整得到x的百位数（bai），即int bai=x/100;
将得到的各个数位上的数字按照新的顺序（原百位->个位，原十位->十位，原个位->百位）重新组合成一个新的整数，即g100 + s10 + b。

	g=x%10;
	s=x/10%10;
	b=x/100%10;

5.输出结果

使用cout将重新组合后的整数输出到显示器。
主函数返回0，表示程序正常结束。

	cout<<g*100+s*10+b;
	return 0;

完整代码如下：

#include<iostream> // 引入C++标准输入输出流库，用于进行输入输出操作


using namespace std; // 使用标准命名空间std，简化对标准库函数的调用

int main(){ // 程序主入口函数
    // 定义变量 
    int x, g, s, b; // 定义整型变量x用于存储输入的三位整数，g用于存储个位数，s用于存储十位数，b用于存储百位数
    
    // 输入数据
    cin>>x; // 从标准输入（如键盘）读取一个三位整数并将其赋值给变量x
    
    // 数据计算与处理
    g = x % 10; // 计算并获取x的个位数
    s = x / 10 % 10; // 计算并获取x的十位数
    b = x / 100 % 10; // 计算并获取x的百位数

    // 将提取出的各个数位上的数字重新排列（将原百位、十位、个位分别调整为新数的个位、十位、百位）
    // 这里通过乘以10的相应次方来实现位置调整
    int rearranged_number = g * 100 + s * 10 + b;
    
    // 输出数据
    cout<<rearranged_number; // 输出重新排列后的整数到标准输出（如显示器）

    return 0; // 主函数返回0，表示程序正常结束
} // 结束main函数

问题：1390-请从键盘读入一个四位整数，求这个四位整数各个位的和是多少？

类型：基础问题、拆位求解。

题目描述：

请从键盘读入一个四位整数，求这个四位整数各个位的和是多少？

输入：

一个四位整数 n 。

输出：

这个四位数各个位的和。

样例：

输入：

输出：

在这里插入图片描述

1.分析问题

已知：一个四位整数 n 。
未知：这个四位数各个位的和。
关系：拆位求解

2.定义变量

定义整型变量x用于存储输入的四位整数，g用于存储个位数，s用于存储十位数，b用于存储百位数，q用于存储千位数。

	int x,g,s,b,q;

3.输入数据

通过cin从键盘获取用户输入的四位整数，并将其赋值给变量x。

	cin>>x;

4.数据计算

计算并分别提取x的个位、十位、百位和千位数，方法是利用取模和除法运算。

	g=x%10;
	s=x/10%10;
	b=x/100%10;
	q=x/1000%10;

5.输出结果

使用cout将各数位之和输出到显示器。
主函数返回0，表示程序正常结束。

	cout<<g+s+b+q;
	return 0;

完整代码如下：

#include<iostream> // 引入C++标准输入输出流库，提供cin和cout等功能

using namespace std; // 使用标准命名空间std，简化对库函数的调用

int main() { // 程序主入口函数
    // 定义变量 
    int x, g, s, b, q; // 定义整型变量x用于存储输入的四位整数，g、s、b、q分别用于存储个位、十位、百位和千位数字
    
    // 输入数据
    cin>>x; // 从标准输入（如键盘）读取一个四位整数并将其赋值给变量x
    
    // 数据计算与提取各个数位上的数字
    g = x % 10; // 计算并获取x的个位数
    s = (x / 10) % 10; // 计算并获取x的十位数
    b = (x / 100) % 10; // 计算并获取x的百位数
    q = x / 1000; // 计算并获取x的千位数（这里无需再进行取模运算，因为已确保输入的是四位数）
    
    // 各数位数字求和
    int sum_of_digits = g + s + b + q;
    
    // 输出数据
    cout<<sum_of_digits; // 输出各数位之和到标准输出（如显示器）

    return 0; // 主函数返回0，表示程序正常结束
} // 结束main函数

问题：1109 - 加密四位数

类型：基础问题、拆位求解

题目描述：

某军事单位用 4 位整数来传递信息，传递之前要求先对这个 4 位数进行加密。加密的方式是每一位都先加上 5 然后对 10 取余数，再将得到的新数颠倒过来。
例如：原数是 1379 ，那么每位加 5 对 10 取余数的结果为 6824 ，然后颠倒该数，得到新数：4286。
再比如：原数是 2570，那么每位加 5 对 10 取余数的结果为 7025 ，然后颠倒该数，得到新数： 5207 。
请根据加密要求，写出加密算法！

输入：

加密前的 4 位数。

输出：

加密后的结果。

样例：

输入：

输出：

在这里插入图片描述

1.分析问题

已知：加密前的 4 位数。
未知：加密后的结果。
关系：拆位求解再做运算。

2.定义变量

	int x,g,s,b,q;

3.输入数据

通过cin从键盘获取用户输入的整数，并将其赋值给变量x。

	cin>>x;

4.数据计算

使用取模运算符 % 和除法运算符 / 来分离出原四位整数 x 的各个数位。例如，g = x % 10; 得到个位数，s = (x / 10) % 10; 得到十位数，以此类推得到百位和千位数。

	g=x%10;
	s=x/10%10;
	b=x/100%10;
	q=x/1000%10;

对于每一位数字，先加上5，然后对其结果取模10，这样可以确保每位数字仍保持在0到9之间。例如，g=(g+5)%10; 更新了经过变换后的个位数。

	g=(g+5)%10;
	s=(s+5)%10;
	b=(b+5)%10;
	q=(q+5)%10;

5.输出结果

	cout<<g*1000+s*100+b*10+q;
	return 0;

完整代码如下：

// 引入iostream库，以便进行输入输出操作
#include<iostream>

// 使用标准命名空间std，简化对库函数的调用
using namespace std;

int main() {
    // 定义变量：x用于存储输入的四位整数，g、s、b、q分别用于存储个位、十位、百位和千位数字
    int x, g, s, b, q;

    // 输入数据：从用户通过键盘输入一个四位整数，并将其赋值给变量x
    cin>>x;

    // 计算并提取各个数位上的数字
    g = x % 10;          // 获取x的个位数
    s = (x / 10) % 10;   // 获取x的十位数
    b = (x / 100) % 10;  // 获取x的百位数
    q = x / 1000;        // 获取x的千位数（这里无需取模运算，因为四位数的千位就是除以1000的商）

    // 对各数位数字加上5后取模10，确保结果仍在0-9范围内
    g = (g + 5) % 10;
    s = (s + 5) % 10;
    b = (b + 5) % 10;
    q = (q + 5) % 10;




    // 输出数据：将重新组合后的整数输出到显示器
    cout<<g * 1000 + s * 100 + b * 10 + q;

    // 主函数返回0，表示程序正常结束
    return 0;
}

四、总结

本节详细探讨了变量交换与拆位求解这两个在程序设计中不可或缺的概念和技术。首先，我们深入理解了变量交换的重要性及其应用场景，认识到在诸如排序、查找、数据结构操作等过程中，正确且高效地交换变量值是保证程序正确运行的关键环节。针对变量交换，我们介绍了三种有效的方法：

临时变量法：通过引入一个额外的临时变量暂存其中一个待交换变量的值，从而实现安全、直观的交换过程。尽管这种方法略显繁琐，但其逻辑清晰，不易出错，尤其适用于初学者和对代码可读性要求较高的场合。
加法交换律法：利用加法交换律的性质，通过一系列加法和减法操作，巧妙地在不借助额外变量的情况下实现变量值的互换。这种方法虽然巧妙且无需额外内存开销，但逻辑相对复杂，对初学者理解难度较高，更适合用于锻炼逻辑思维能力和数学应用能力。
swap函数法：利用C++标准库提供的swap函数，简洁、高效地完成变量交换。这种方法封装了交换逻辑，使用便捷，但对初学者而言可能隐藏了底层交换过程，不利于深入理解交换原理。

在拆位求解部分，我们首先明确了数位的概念，理解了十进制数的各个数位所对应的权重和含义。接着，通过复习数学中的除法和取余运算，我们掌握了如何通过简单的算术操作提取一个数的个位、十位乃至更高位的数字。拆位求解能力不仅在处理特定数学问题时发挥作用，而且对于理解整数内部结构、编写与整数数位相关的算法具有重要意义。

综上所述，掌握变量交换与拆位求解不仅是NOI竞赛学习的重要环节。通过本节的学习与实践，读者应能够灵活运用各种交换方法，解决实际编程中的变量交换需求，并具备将一个整数按数位进行拆分、求和等操作的能力。这些知识将为后续深入学习算法、数据结构及更复杂的编程任务打下坚实基础。