文章目录
- week34 VBAED
- 摘要
- Abstract
- 一、文献阅读
- 1. 题目
- 2. abstract
- 3. 网络架构
- 3.1 序列问题阐述
- 3.2 变分模态分解
- 3.3 具有 BiLSTM 和双向输入注意力的编码器
- 3.4 具有 BiLSTM 和双向时间注意力的解码器
- 4. 文献解读
- 4.1 Introduction
- 4.2 创新点
- 4.3 实验过程
- 4.3.1 数据集
- 数据预处理
- 评估指标
- 实验结果分析
- 总结
- 参考文献
week34 VBAED
摘要
本周阅读了题为Accurate water quality prediction with attention-based bidirectional LSTM and encoder–decoder的论文。该文提出了一种称为VBAED的混合预测方法来预测水质时间序列。VBAED 结合了变分模式分解 (VMD)、双向输入注意力机制、具有双向 LSTM 的编码器 (BiLSTM) 以及具有双向时间注意力机制和 BiLSTM 的解码器。VBAED 的定义是一个编码器-解码器模型,它使用 VMD 作为模式分解,将 BiLSTM 与双向注意力机制相结合。本文在最后使用vmdpy对数据进行了一定处理。
Abstract
This week read the paper entitled Accurate water quality prediction with attention-based bidirectional LSTM and encoder–decoder. This paper proposes a hybrid prediction method called VBAED to predict the water quality time series. VBAED combines Variational mode decomposition (VMD), a Bidirectional input Attention mechanism, an Encoder with bidirectional LSTM (BiLSTM), and a Decoder with a bidirectional temporal attention mechanism and BiLSTM. The definition of VBAED is an Encoder–Decoder model that uses VMD as mode decomposition, combining BiLSTM with a bidirectional attention mechanism. And the end, using vmdpy as a tool for processing data.
一、文献阅读
1. 题目
标题:Accurate water quality prediction with attention-based bidirectional LSTM and encoder–decoder
作者:Jing Bi, Zexian Chen, Haitao Yuan, Jia Zhang
期刊名:[Expert Systems with Applications]
链接:https://doi.org/10.1016/j.eswa.2023.121807
2. abstract
随着水质数据的增加,其变得不稳定且高度非线性,因此,其准确预测成为一个巨大的挑战。为了解决这个问题,该文提出了一种称为VBAED的混合预测方法来预测水质时间序列。VBAED 结合了变分模式分解 (VMD)、双向输入注意力机制、具有双向 LSTM 的编码器 (BiLSTM) 以及具有双向时间注意力机制和 BiLSTM 的解码器。VBAED 的定义是一个编码器-解码器模型,它使用 VMD 作为模式分解,将 BiLSTM 与双向注意力机制相结合。
As the water quality data increases, it becomes unstable and highly nonlinear, and therefore, its accurate prediction becomes a big challenge. To solve it, this work proposes a hybrid prediction method called VBAED to predict the water quality time series. VBAED combines Variational mode decomposition (VMD), a Bidirectional input Attention mechanism, an Encoder with bidirectional LSTM (BiLSTM), and a Decoder with a bidirectional temporal attention mechanism and BiLSTM. The definition of VBAED is an Encoder–Decoder model that uses VMD as mode decomposition, combining BiLSTM with a bidirectional attention mechanism.
3. 网络架构
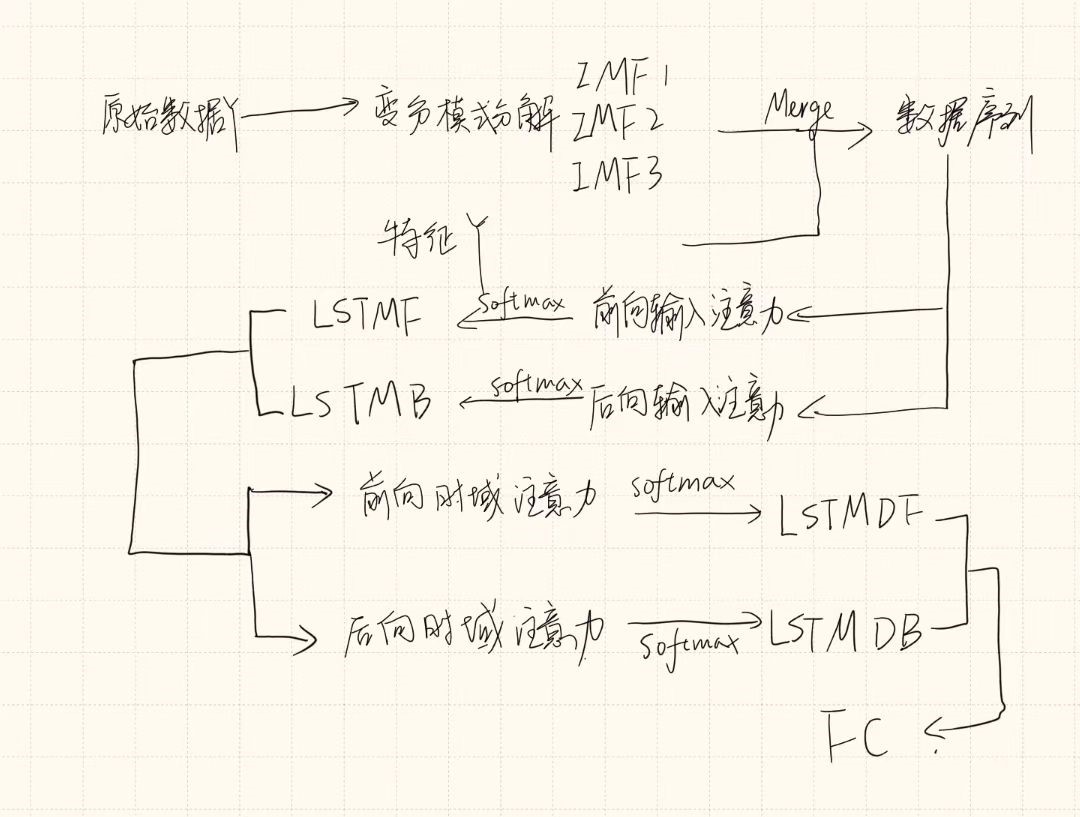
该文在输入维度和时间维度上创新地将注意力机制与BiLSTM相结合,并采用VMD对水质数据进行分解,将重要模式与噪声模式分离,进一步提高预测精度。具体来说,通过VMD将预测因子的历史数据分解为多种模式。然后,模式和其他特征由具有双向输入注意机制的 BiLSTM 进行编码,并由具有双向时间注意机制的 BiLSTM 进行解码,以产生最终预测。
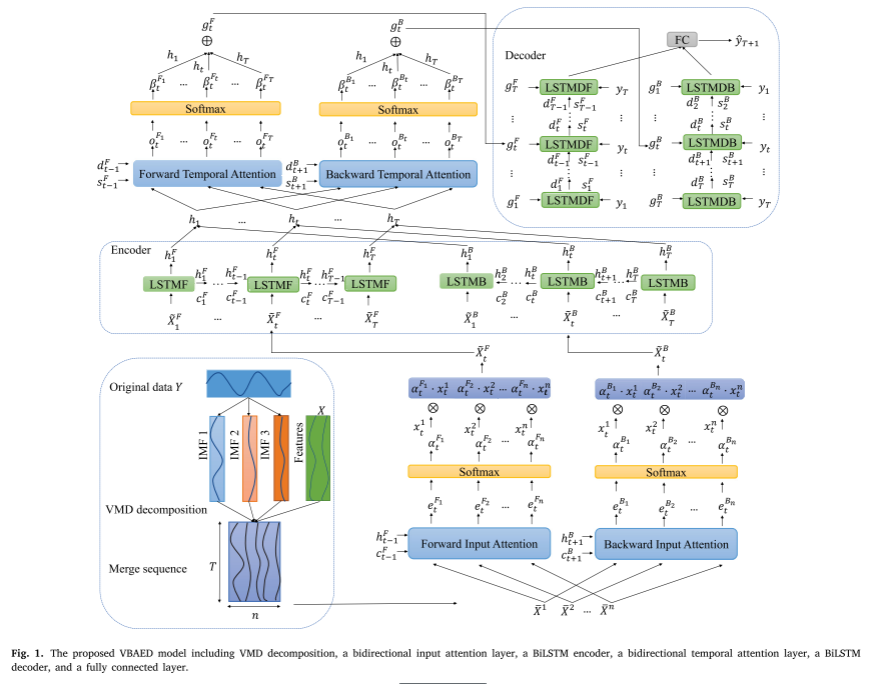
上图说明了所提出的 VBAED 模式
3.1 序列问题阐述

3.2 变分模态分解
VMD迭代地搜索变分模态的最优解,不断更新每个模态函数和中心频率,并获得多个本征模态函数(IMF)。变分问题定义为求解 k模IMF 来最小化每种模式的估计带宽之和。 Y 分解为 k 模。
VMD分解可以降低时间序列的非线性和波动性,避免模式混合的负面影响。不同的模态分量对预测结果有不同的影响。
通过将它们分离并与输入注意机制相结合,VBAED 能够自适应地选择重要模式,从多个模式中过滤掉噪声模式,并专注于包含重要信息的模式。可以根据实验结果选择性地去除模态分量。
这项工作通过 VMD 将目标值序列分解为三个分量,并将其用作特征。这引导神经网络更用心地学习更复杂的特征并提高预测精度。VMD处理后的的输入为 X ^ = { X ^ 1 , … , X ^ t , … , X ^ T } ∈ R n × T where n = n ˙ + 3 \hat X=\{\hat X_1,\dots, \hat X_t,\dots,\hat X_T\}\in \mathbb R^{n\times T}\ \text{where}\ n=\dot n+3 X^={X^1,…,X^t,…,X^T}∈Rn×T where n=n˙+3
3.3 具有 BiLSTM 和双向输入注意力的编码器
BiLSTM:由两个独立的 LSTM 单元组成。第一个 LSTM 单元称为 LSTMF,它从前到后对信息进行编码。第二个 LSTM 单元称为 LSTMB,它从后到前对信息进行编码。然后,组合来自两个方向的信息以获得编码器在时间步 t 的隐藏状态 h t h_t ht。
特别是,在时间步 t 处,LSTMF 根据时间步 t-1 处的前一个隐藏状态
h
t
−
1
F
h^F_{t-1}
ht−1F、时间步 t-1 处的单元状态
c
t
−
1
F
c^F_{t-1}
ct−1F以及输入
X
t
X_t
Xt 计算其隐藏状态
h
t
F
h^F_t
htF 。 LSTMB 基于隐藏状态
h
t
−
1
B
h^B_{t-1}
ht−1B、单元状态
c
t
+
1
B
c^B_{t+1}
ct+1B 和输入
X
t
X_t
Xt 计算其隐藏状态
h
t
B
h^B_t
htB。然后,将前向隐藏状态
h
t
F
h^F_t
htF和后向隐藏状态
h
t
B
h^B_t
htB组合成BiLSTM的隐藏状态。 LSTMF和LSTMB是两个独立的LSTM单元,它们不共享参数。
h
t
F
h^F_t
htF 、
h
t
B
h^B_t
htB 和
h
t
h_t
ht 给出为:
h
t
F
=
LF
(
h
t
−
1
F
,
c
t
−
1
F
,
X
^
t
)
(2)
h^F_t=\text{LF}(h^F_{t-1},c^F_{t-1},\hat X_t) \tag{2}
htF=LF(ht−1F,ct−1F,X^t)(2)
h t B = LB ( h t + 1 B , c t + 1 B , X ^ t ) (3) h^B_t=\text{LB}(h^B_{t+1},c^B_{t+1},\hat X_t) \tag{3} htB=LB(ht+1B,ct+1B,X^t)(3)
h t = [ h t F ; h t B ] (4) h_t=[h^F_t;h^B_t] \tag{4} ht=[htF;htB](4)
其中 LF 是 LSTMF 单元,LB 是 LSTMB 单元。 𝑚 表示每个 BiLSTM 单元的隐藏状态大小, h t F ∈ R m , h t B ∈ R m , h t ∈ R 2 m h^F_t\in R^m,\ h^B_t\in R^m,\ h_t\in R^{2m} htF∈Rm, htB∈Rm, ht∈R2m
该文为BiLSTM设计了一种输入注意机制。分别为LSTMF和LSTMB添加一个输入注意机制层,两种输入注意力机制关注不同的特征。


3.4 具有 BiLSTM 和双向时间注意力的解码器
BiLSTM 解码器由两个独立的 LSTM 单元组成,包括 LSTMDF 和 LSTMDB。前者从前往后解码信息,后者从后到前解码信息。
m 表示每个 BiLSTM 单元的隐藏状态大小。 hi 表示编码器的第 i 隐藏状态。
BiLSTM中双向注意力机制的详细信息:
时间步 t 的前向注意力权重和第 i 个隐藏状态 ( h i h_i hi) 的后向注意力权重分别由 β t F i ( β t F i ∈ ( 0 , 1 ) ) , β t B + i ( ∈ ( 0 , 1 ) ) \beta^{F_i}_t(\beta^{F_i}_t\in(0,1)),\ \beta^{B+i}_t(\in(0,1)) βtFi(βtFi∈(0,1)), βtB+i(∈(0,1)) 。 β t F i \beta^{F_i}_t βtFi 是根据 LSTMDF 在时间步 t-1 的隐藏状态 d t − 1 f ( d t − 1 F ∈ R p ) d^f_{t-1}(d^F_{t-1}\in R^p) dt−1f(dt−1F∈Rp)和单元状态 s t − 1 F ( s t − 1 F ∈ R p ) s^{F}_{t-1}(s^F_{t-1}\in R^p) st−1F(st−1F∈Rp)计算的。此外, β t B i \beta^{B_i}_t βtBi是根据LSTMDB在时间步t+1的隐藏状态 d t + 1 B ( d t + 1 B ∈ R p ) d^B_{t+1}(d^B_{t+1}\in R^p) dt+1B(dt+1B∈Rp)和单元状态 s t + 1 B ( s t + 1 B ∈ R p ) s^B_{t+1}(s^B_{t+1}\in R^p) st+1B(st+1B∈Rp)计算的。 o t F i o^{F_i}_t otFi 和 o t B i o^{B_i}_t otBi 表示 h i h_i hi 在时间步 t 的能量得分,其公式如下:


时间步 𝑡 处的前向和后向上下文向量由 g t F g^F_t gtF 和 g t B g^B_t gtB 表示,它们分别是编码器所有隐藏状态的加权和

将 g t F g^F_t gtF 和 g t B g^B_t gtB 同历史真实值 y t y_t yt联立,分别在时间t获得LSTMDF和LSTMDB的新输入 y ~ t F , y ~ t B \tilde y^F_t, \tilde y^B_t y~tF,y~tB

将这些输入用于更新LSTMDF和LSTMDB在时间步t处的隐藏状态 d t F , d t B d^F_t, d^B_t dtF,dtB

其中LDF表示LSTMDF,LDB表示LSTMDB
最终预测值 y ^ t + 1 \hat y_{t+1} y^t+1表示为
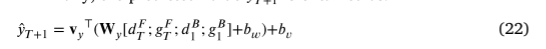
训练过程:采用均方误差MSE作为损失函数,以最小化真实值与预测值之间的差异。损失函数
Δ
\Delta
Δ如下:

4. 文献解读
4.1 Introduction
LSTM只能从前到后进行编码,无法捕获从后道歉的信息。同时,采用注意力机制的网络也无法捕获从后到前的数据。另外,水质数据中可能包含噪声,而噪声无法通过上述方法分离。为了解决上述问题,该文提出了一种称为 VBAED 的混合方法。 VBAED 集成了变分模式分解(VMD)、双向输入注意力机制、具有双向 LSTM 的编码器(BiLSTM)以及具有双向时间注意力机制和 BiLSTM 的解码器。
4.2 创新点
- 采用 BiLSTM 作为编码器来捕获两个方向的特征。 BiLSTM 通过双向输入注意力机制进行了改进,以独立地从两个方向为输入添加注意力权重。
- 采用 BiLSTM 作为解码器,结合双向时间注意力机制来捕获长期依赖性,从而在所有时间步上自适应地选择编码器的重要隐藏状态,并从两个方向对其进行解码。
4.3 实验过程
4.3.1 数据集
为了评估不同时间序列预测方法的性能,采用了两种不同的真实数据集,即BTH数据集和亚拉巴马数据集,分别为多特征和单特征数据集。
-
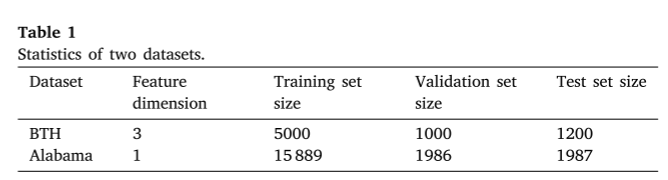
BTH数据集收集自2018年9月至2021年12月期间京津冀地区河流中的自动水质站。每4 h采集一次,涉及pH、TN、TP。在实验中,TN被用作基础事实,pH和TP被用作特征。对于少量的缺失值,采用线性插值的方法进行补充,总共有7200个数据样本。我们将前5000个数据样本作为训练集,接下来的1000个数据样本作为验证集,剩下的1200个数据样本作为测试集。
-
亚拉巴马数据集是2017年5月至2019年8月美国亚拉巴马河一段的水质数据。数据收集间隔为一小时。与BTH数据集不同,亚拉巴马数据集只有一个DO特征,即亚拉巴马数据集中的目标值。对于数据集中的少量缺失值,采用线性插值方法进行补齐。在亚拉巴马数据集中,我们总共有19862个数据样本。在这项工作中,我们将前15889个数据样本作为训练集,随后的1986个数据样本作为验证集,最后的1987个数据样本作为测试集。
数据预处理
采用Savitzky Golay(SG)滤波器对BTH数据集中TN、TP和pH的时间序列数据进行平滑处理,以减少噪声的干扰和局部异常值对整体趋势的影响。对于亚拉巴马数据集,我们直接预测目标DO值而不进行任何预处理。
评估指标
为了验证VBAED的性能,采用三个评估指标来比较预测精度,即均方根误差(RMSE)、平均绝对误差(MAE)和决定系数(R2)。
实验结果分析
- 验证VBAED的准确性
用训练集对VBAED进行训练,对于BTH数据集,预测曲线和地面实况曲线几乎相同,这表明VBAED在多特征数据集中是有效的。对于亚拉巴马数据集,VBAED在单特征数据集中也工作得很好。
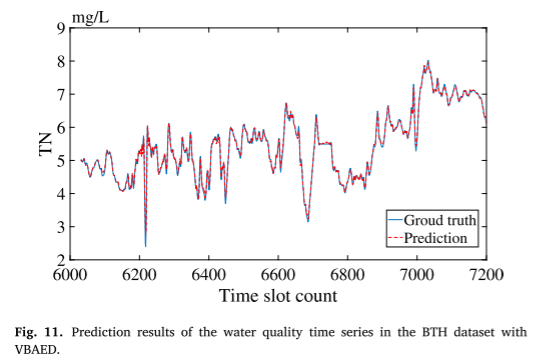
在BTH数据集上的水质时间序列预测结果
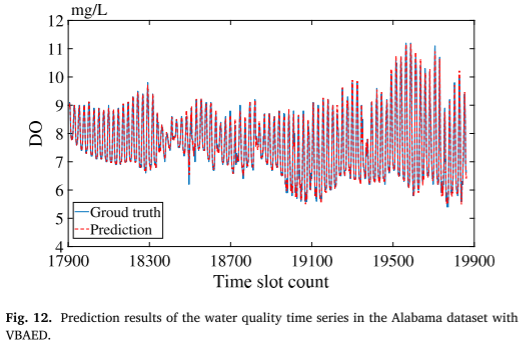
- 验证VBAED的鲁棒性和有效性
为了进一步,采用RMSE,MAE和R2将其与其他10个对等体进行比较,(DA-RNN只能用于多特征数据集)结果表明,VBAED在BTH和亚拉巴马数据集上都获得了最好的结果。此外,在BTH数据集中,当不采用VMD分解时,LSTM,BiLSTM和DA-RNN的RMSE分别为0.2093,0.1657和0.1259。采用VMD分解后,VMD-LSTM、VMD-BiLSTM和VDM-DARNN的RMSE分别为0.1688、0.1475、0.1156。在亚拉巴马数据集中,当不采用VMD分解时,LSTM和BiLSTM的RMSE分别为0.1957和0.1866。采用该方法后,VMD-LSTM和VMD-BiLSTM的RMSE分别为0.1724和0.1555。结果表明,VMD有效地把握了水质数据的演变趋势,并将其分解为关键信息模式和噪声模式,有助于模型训练,提高了预测精度。在BTH和亚拉巴马数据集上,LSTM的RMSE都比BiLSTM差,这表明双向LSTM结构克服了传统LSTM容易忽略从后到前的信息,导致相关信息丢失的局限性。


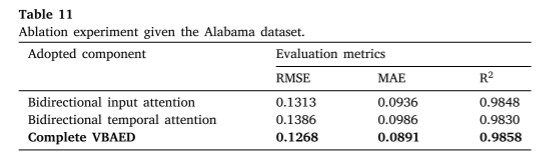
- 验证双向输入注意机制和双向时间注意机制的效果
在两个数据集上进行了消融实验。仅应用双向输入注意机制或双向时间注意机制会导致预测精度显著降低。在BTH和亚拉巴马数据集上,采用双向输入注意的模型的RMSE分别为0.0705和0.1313,而采用双向时间注意的模型的RMSE分别为0.0768和0.1368。这表明双向输入注意机制在VBAED中比双向时间注意机制起着更重要的作用。对于原始的长序列数据,网络很难直接捕捉到重要信息。双向输入注意机制使VBAED能够区分原始特征的重要性,从而加强重要特征,削弱不重要特征。此外,它使VBAED中的编码器能够获得更多有用的信息。VBAED采用双向输入注意机制提取相关特征,采用双向时间注意机制选择所有时间步的相关隐藏状态。因此,VBAED在BTH和亚拉巴马数据集的所有方法中实现了最高的预测精度。

import numpy as np
import matplotlib.pyplot as plt
from vmdpy import VMD
# -----测试信号及其参数--start-------------
Fs=1000 # 采样频率
N=1000 # 采样点数
t=np.arange(1,N+1)/N
fre_axis=np.linspace(0,Fs/2,int(N/2))
f_1=100;f_2=200;f_3=300
v_1=(np.cos(2*np.pi*f_1*t));v_2=1/4*(np.cos(2*np.pi*f_2*t));v_3=1/16*(np.cos(2*np.pi*f_3*t))
v=[v_1,v_2,v_3] # 测试信号所包含的各成分
f=v_1+v_2+v_3+0.1*np.random.randn(v_1.size) # 测试信号
# -----测试信号及其参数--end----------
# alpha 惩罚系数;带宽限制经验取值为抽样点长度1.5-2.0倍.
# 惩罚系数越小,各IMF分量的带宽越大,过大的带宽会使得某些分量包含其他分量言号;
# a值越大,各IMF分量的带宽越小,过小的带宽是使得被分解的信号中某些信号丢失该系数常见取值范围为1000~3000
alpha=2000
tau=0 # tau 噪声容限,即允许重构后的信号与原始信号有差别。
K=3 # K 分解模态(IMF)个数
DC=0 # DC 若为0则让第一个IMF为直流分量/趋势向量
init=1 # init 指每个IMF的中心频率进行初始化。当初始化为1时,进行均匀初始化。
tol=1e-7 # 控制误差大小常量,决定精度与迭代次数
u, u_hat, omega = VMD(f, alpha, tau, K, DC, init, tol) # 输出U是各个IMF分量,u_hat是各IMF的频谱,omega为各IMF的中心频率
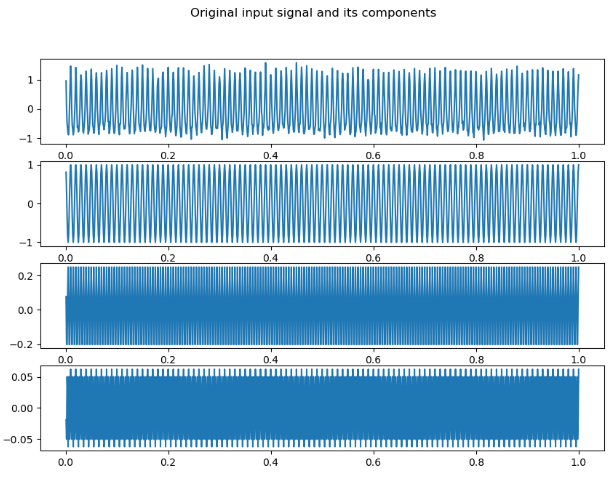
# 1 画原始信号和它的各成分
plt.figure(figsize=(10,7));plt.subplot(K+1, 1, 1);plt.plot(t,f)
for i,y in enumerate(v):
plt.subplot(K+1, 1, i+2);plt.plot(t,y)
plt.suptitle('Original input signal and its components');plt.show()
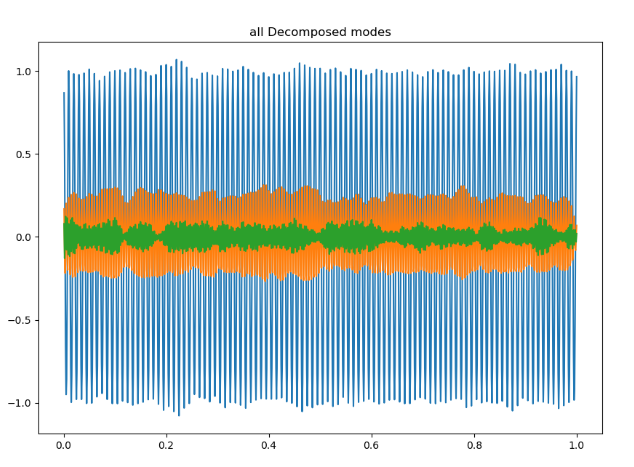
# 2 分解出来的各IMF分量
plt.figure(figsize=(10,7))
plt.plot(t,u.T);plt.title('all Decomposed modes');plt.show() # u.T是对u的转置
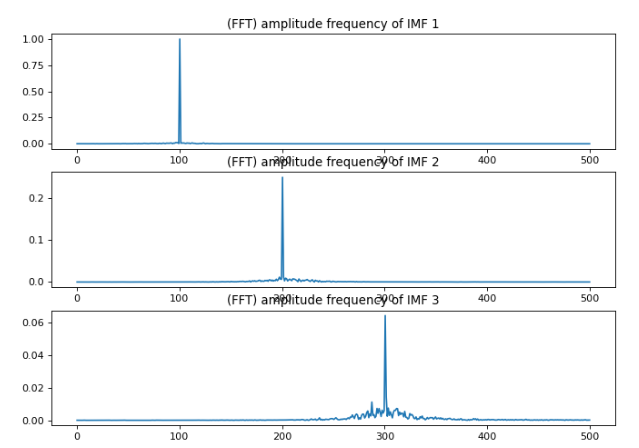
# 3 各IMF分量的fft幅频图
plt.figure(figsize=(10, 7), dpi=80)
for i in range(K):
plt.subplot(K, 1, i + 1)
fft_res=np.fft.fft(u[i, :])
plt.plot(fre_axis,abs(fft_res[:int(N/2)])/(N/2))
plt.title('(FFT) amplitude frequency of IMF {}'.format(i + 1))
plt.show()
# 4 分解出来的各IMF分量的频谱
# print(u_hat.shape,t.shape,omega.shape)
plt.figure(figsize=(10, 7), dpi=80)
for i in range(K):
plt.subplot(K, 1, i + 1)
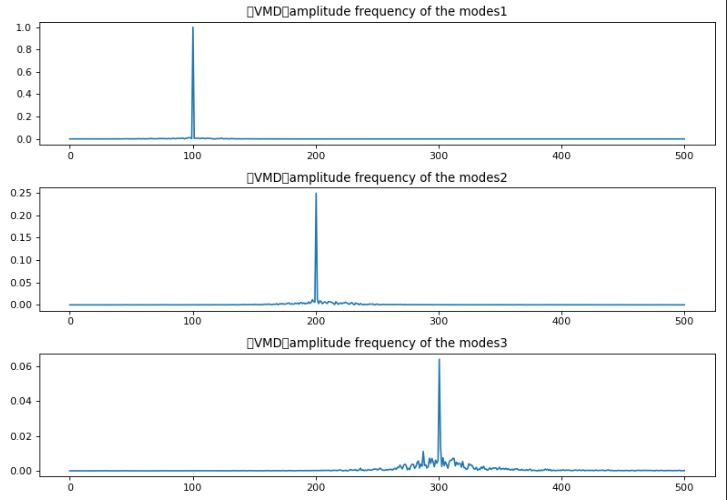
plt.plot(fre_axis,abs(u_hat[:, i][int(N/2):])/(N/2))
plt.title('(VMD)amplitude frequency of the modes{}'.format(i + 1))
plt.tight_layout();plt.show()
# 5 各IMF的中心频率
plt.figure(figsize=(12, 7), dpi=80)
for i in range(K):
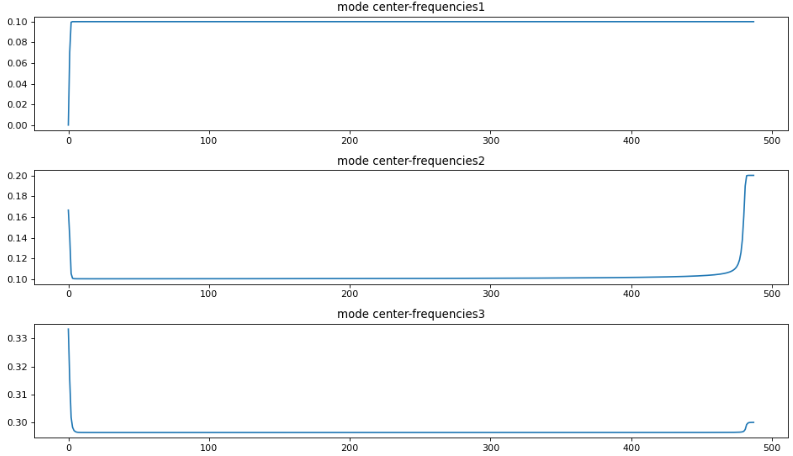
plt.subplot(K, 1, i + 1)
plt.plot(omega[:,i]) # X轴为迭代次数,y轴为中心频率
plt.title('mode center-frequencies{}'.format(i + 1))
plt.tight_layout();plt.show()
plt.figure(figsize=(10,7))
plt.plot(t,np.sum(u,axis=0))
plt.title('reconstructed signal')
总结
这周通过文献学习了解了EMD和VMD两种模态分解方法,模态分解方法可对预测因子的历史数据进行分解,其中VMD分解可以降低时间序列的非线性和波动性,不同于EMD,它可以避免模式混合的负面影响。不同的模态分量对预测结果有不同的影响,通过将它们分离并与输入注意机制相结合,VBAED具有自适应选择重要模式的能力,从多个模式中过滤掉噪声模式,并关注包含重要信息的模式,这将引导神经网络更专注地学习更复杂的特征,从而能够提高预测精度。
参考文献
[1] Jing Bi, Zexian Chen, Haitao Yuan, Jia Zhang “Accurate water quality prediction with attention-based bidirectional LSTM and encoder–decoder”, [J] https://doi.org/10.1016/j.eswa.2023.121807