C++ - 二叉搜索树的基本实现

news2024/11/23 8:04:03

目录

0. 引言

1. 二叉搜索树

1.1 定义

1.2 特点

2. 二叉搜索树的实现 

2.1 基本框架 

 2.2 查找

2.3 插入 

2.4 删除 

2.4.1 右子树为空

 2.4.2 左子树为空

2.4.3 左右都不为空 

2.4.4 代码

0. 引言

在C语言数据结构中，我们已经基本了解过二叉树，这篇博客分享的二叉搜索树，主要是为了方便学习后面的 map 以及 set 的学习。那么，现在让我们开始吧！

1. 二叉搜索树

1.1 定义

 二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值；

若它的右子树不为空，则右子树上所有节点的值都大于根节点的值；

它的左右子树也分别为二叉搜索树。

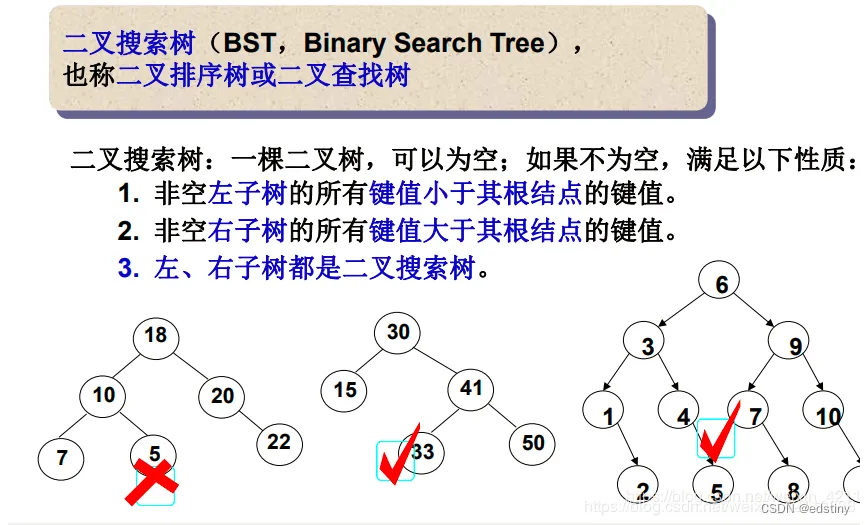
这里我们可以看到，将数据存入二叉搜索树中进行查找时，理想情况下只需要 logN 的时间复杂度。这就是 二叉搜索树 名字的由来，搜索（查找）速度很快。

1.2 特点

搜索二叉树的基本特点：左比根小，右比根大。

  • 若某个节点的左节点不为空，则左节点的值一定比当前节点的值小，且其左子树的所有节点都比它小；
  • 若某个节点的右节点不为空，则右节点的值一定比当前节点的值大，且其右子树的所有节点都比它大；
  • 二叉搜索树的每一个节点的根，左，右 都满足基本特点。

除此之外，二叉搜索树还有一个特点： 中序遍历的结果为升序

例如，对下面这个搜索二叉树进行中序遍历： 

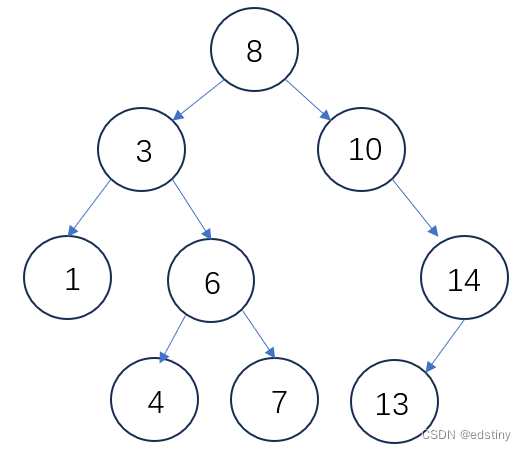
上述结果为：1  3  4  5  6  7  10  13  14 

由此可见搜素二叉树也具有排序价值，故也称为二叉排序树。 

2. 二叉搜索树的实现 

2.1 基本框架 

我们主要利用C++的类和对象，泛型编程等特点来建立节点的框架，并在此框架的基础上完善各种功能。具体代码如下：

#pragma once

#include <iostream>

//部分展开，避免冲突
using std::cout;	//遍历时需要用到
using std::endl;

//命名空间
namespace LHY
{
	//利用模板，泛型编程
	template<class K>
	struct BSTreeNode
	{
		BSTreeNode(const K& key)
			:_left(nullptr)
			,_right(nullptr)
			,_key(key)
		{}

		//二叉树包含左节点指针、右节点指针、节点值信息
		BSTreeNode<K>* _left;
		BSTreeNode<K>* _right;
		K _key;
	};

	template<class K>
	class BSTree
	{
		typedef BSTreeNode<K> Node;
	private:
		Node* _root = nullptr;	//二叉搜索树的根
	};
}

这里需要注意的是，二叉搜索树的节点类需要写出构造函数，因为后面创建新节点时会用到；二叉搜索树的根可以给个缺省值 nullptr ，确保后续不会出错。

 2.2 查找

查找思路较为简单，当查找值比当前值大，往右子树走，当查找值比当前值小时，则往左走，若相等，即为找到。代码如下：

bool Empty() const
{
	return _root == nullptr;
}

bool Find(const K& key) const
{
	//如果为空，则查找失败
	if (Empty())
		return false;

	Node* cur = _root;
	while (cur)
	{
		//如果查找值比当前值大，则往右走
		if (cur->_key < key)
			cur = cur->_right;
		//如果查找值比当前值小，则往左走
		else if (cur->_key > key)
			cur = cur->_left;
		else
			return true;	//找到了
	}

	return false;	//没找到
}

例如，当我们查找 7 时，只需查找 4 次，即可得到结果。

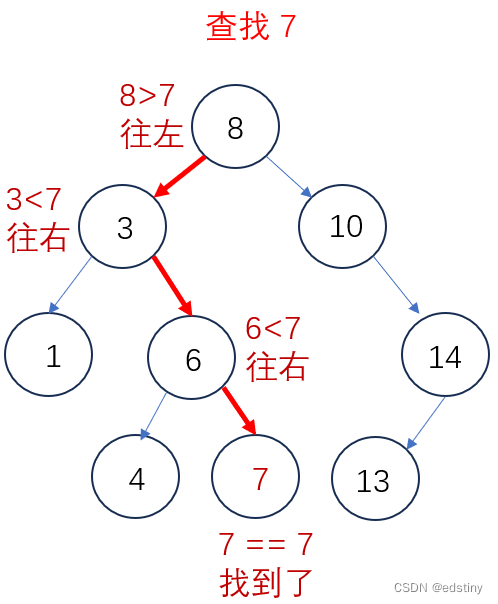
 返回 bool 值是为了表示操作成功或者失败。

2.3 插入 

实现插入操作实际上与查找差不多，插入操作需要先查找合适的位置再进行插入操作。因此我们的思路如下：

  • 先找到合适的位置（满足基本特点）
  • 如果当前位置不为空（冗余），则插入失败
  • 为空则结束循环，进行插入：创建新节点、判断需要插在左边还是右边、链接新节点完成插入

具体代码如下：

bool Insert(const K& key)
{
	//如果为空，则就是第一次插入
	if (Empty())
	{
		_root = new Node(key);
		return true;
	}

	//需要记录父节点
	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			//出现冗余，插入失败
			return false;
		}
	}

	cur = new Node(key);

	//判断需要链接至左边还是右边
	if (parent->_key < key)
		parent->_right = cur;
	else
		parent->_left = cur;

	return true;
}

二叉搜索树的根为多少，取决于谁第一个插入，后序插入的节点都是基于根节点进行插入的

当找到合适位置时，需要根据当前 key 值与父节点的值进行判断，插入至合适的位置（满足基本特点）。

我们以插入 15 为例子，第一步我们先查找合适的位置：

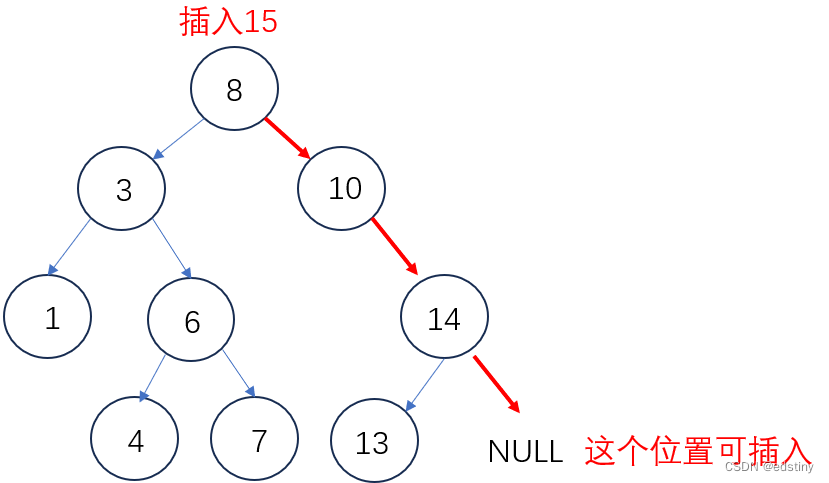
第二步，插入节点：

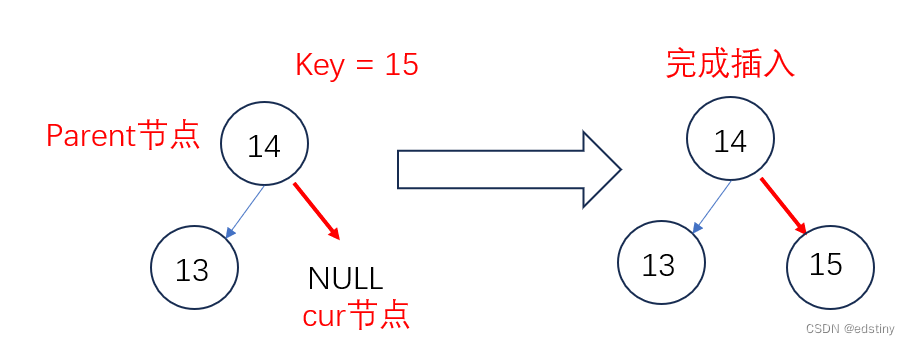
若查找不到合适的位置，则插入失败。 且代码当前实现的二叉搜索树不允许冗余，如果想要实现冗余的二叉搜索树，可以规定重复的值插在左边或右边，都是可行的。

在确认 新节点的链接位置时，可以通过 parent 与 cur 的 key 值判断，也可以通过原有链接关系判断 如果是通过原有链接判断：parent->_right == cur 需要先创建新节点 new_node（不能覆盖 cur 的值），利用 cur 进行链接判断后，再进行新节点链接 推荐直接使用 key 值判断，省时省力

总结： 

  • 在执行循环查找合适位置前，需要创建变量记录父节点的位置，方便后续进行新节点链接
  • 找到合适位置后，需要将新节点与父节点进行比较判断，确认链接在左边还是右边
  • 插入失败返回 false，插入成功返回 true。

2.4 删除 

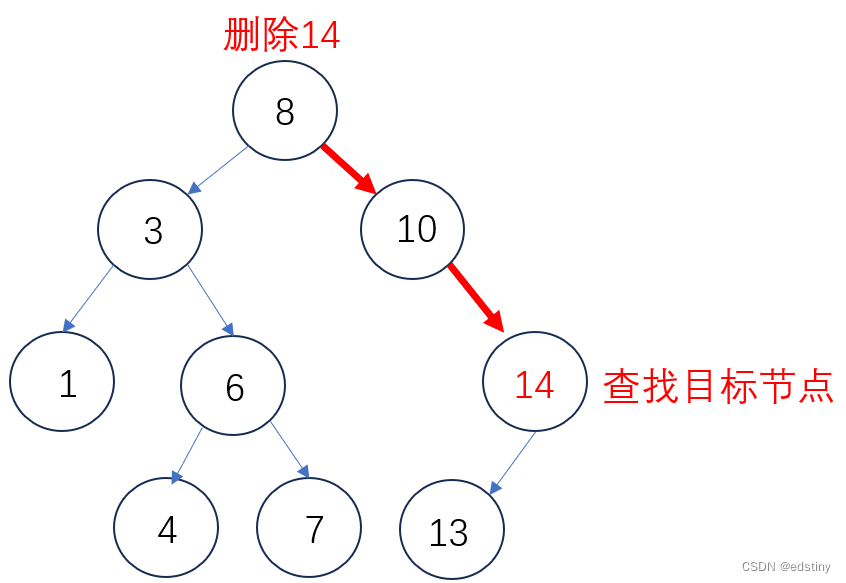
删除的思路如下：先利用查找来判断目标值是否存在，如果存在，则进行删除，此时，待删除的节点可能会存在多种情况，需要具体问题具体分析，如果不存在，则删除失败。下面我们依次来看删除的各种可能性。

2.4.1 右子树为空

当右子树为空时，只 需要将其左子树与父节点进行判断链接即可，无论其左子树是否为空，都可以链接，链接完成后，删除目标节点。

 

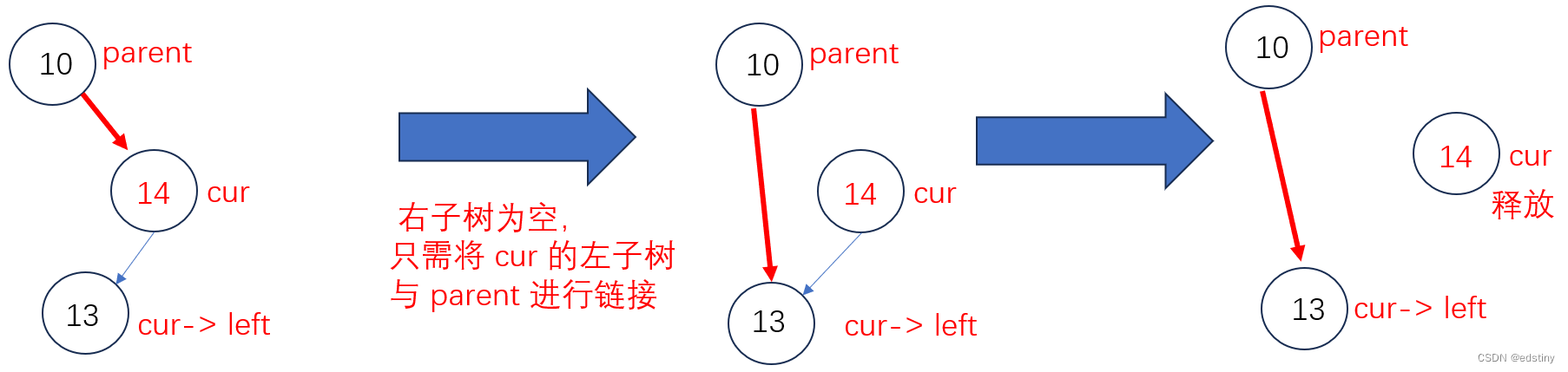
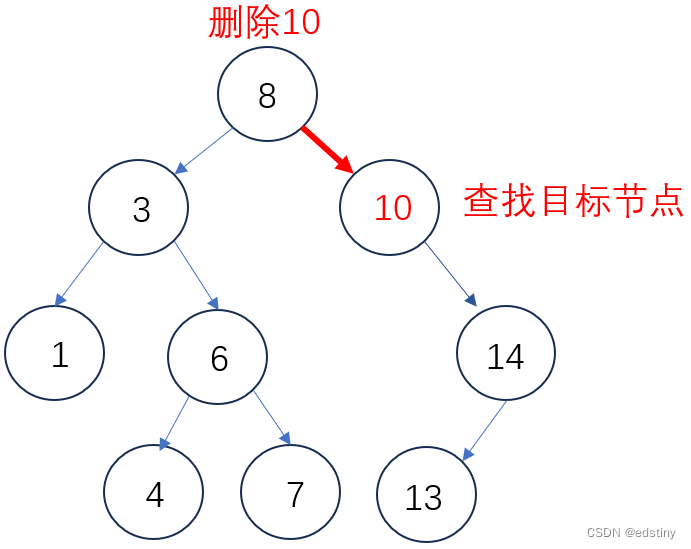
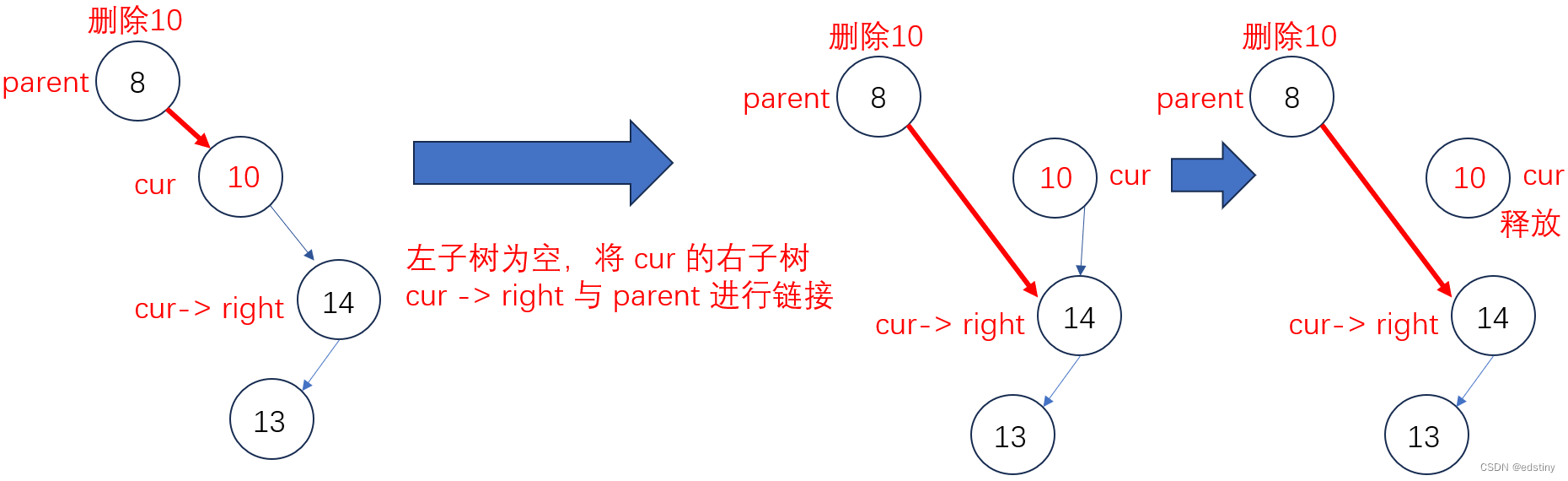
 2.4.2 左子树为空

同理，左子树为空时，将其右子树与父节点进行判断链接，链接完成后删除目标节点。 

 

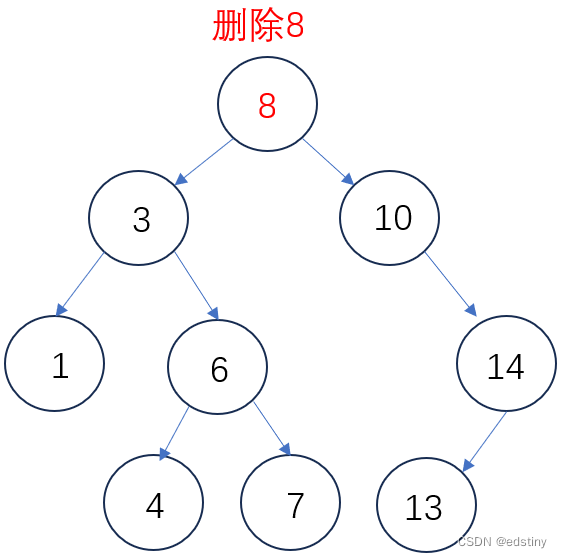
2.4.3 左右都不为空 

当左右都不为空时，就有点麻烦了，需要找到一个合适的值（即 > 左子树所有节点的值，又 < 右子树所有节点的值），确保符合二叉搜索树的基本特点。符合条件的值有：左子树的最右节点（左子树中最大的）、右子树的最左节点（右子树中最小的），将这两个值中的任意一个覆盖待删除节点的值，都能确保符合要求。

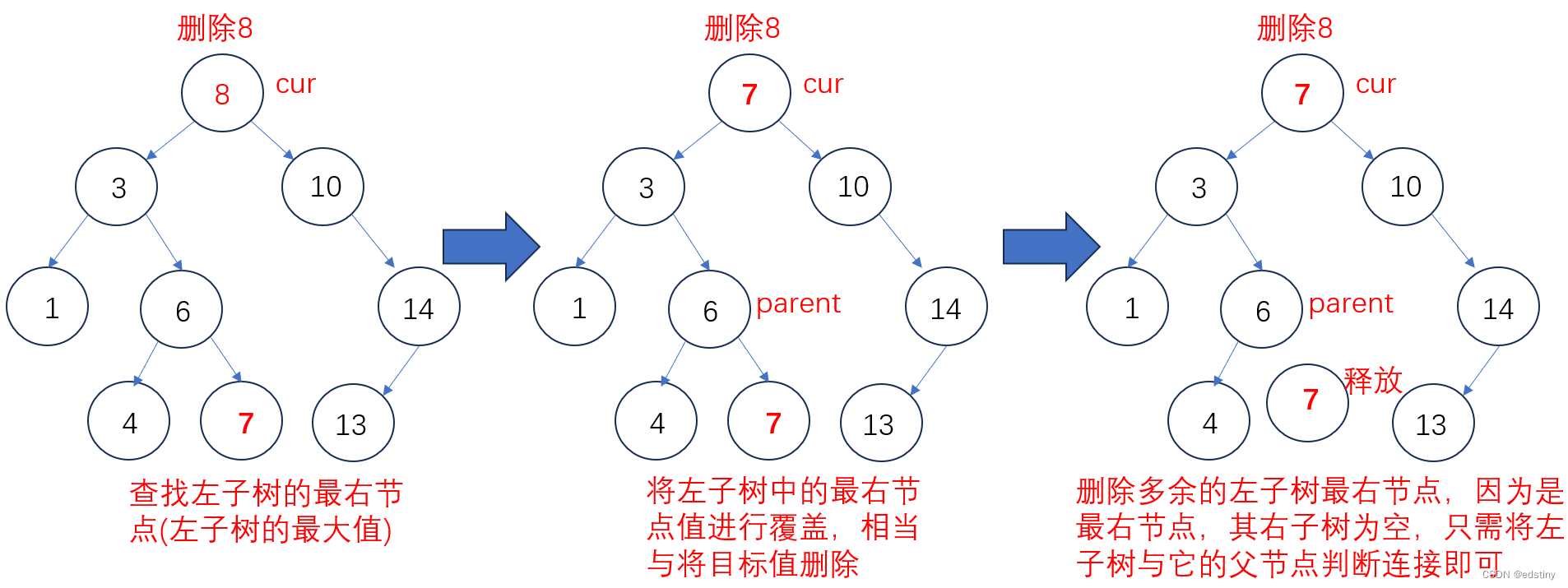
解释： 为什么找 左子树的最右节点或右子树的最左节点的值覆盖 可以符合要求？因为左子树的最右节点是左子树中最大的值，> 左子树所有节点（除了自己），< 右子树所有节点，右子树的最左节点也是如此，都能符合要求。

2.4.4 代码
bool Erase(const K& key)
{
	if (Empty())
		return false;

	Node* parent = nullptr;
	Node* cur = _root;
	while (cur)
	{
		if (cur->_key < key)
		{
			parent = cur;
			cur = cur->_right;
		}
		else if (cur->_key > key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else
		{
			if (cur->_right == nullptr)
			{
				//右为空，考虑将左子树链接
				if (cur == _root)
					_root = cur->_left;
				else
				{
					if (parent->_right == cur)
						parent->_right = cur->_left;
					else
						parent->_left = cur->_left;
				}

				delete cur;
			}
			else if (cur->_left == nullptr)
			{
				//左为空，考虑将右子树链接
				if (cur == _root)
					_root = cur->_right;
				else
				{
					if (parent->_right == cur)
						parent->_right = cur->_right;
					else
						parent->_left = cur->_right;
				}

				delete cur;
			}
			else
			{
				//左右子树都不为空，找左子树的最右节点
				//可以更改为找右子树的最左节点
				parent = cur;
				Node* maxLeft = cur->_left;

				while (maxLeft->_right)
				{
					parent = maxLeft;
					maxLeft = maxLeft->_right;
				}

				//替换，伪删除
				cur->_key = maxLeft->_key;

				if (parent->_right == maxLeft)
					parent->_right = maxLeft->_left;
				else
					parent->_left = maxLeft->_left;

				delete maxLeft;
			}

			return true;
		}
	}

	return false;
}

总结： 

左右子树都为空时：直接删除；左子树、右子树其中一个为空时：托孤，将另一个子树（孩子）寄托给父节点，然后删除自己；左子树、右子树都不空：找一个能挑起担子的保姆，照顾左右两个子树（孩子），然后删除多余的保姆。

注意：涉及更改链接关系的操作，都需要保存父节点的信息；右子树为空、左子树为空时，包含了删除 根节点 的情况，此时 parent 为空，不必更改父节点链接关系，更新根节点信息后，删除目标节点即可，因此需要对这种情况特殊处理；右子树、左子树都为空的节点，包含于 右子树为空 的情况中，自然会处理到；左右子树都不为空的场景中，parent 要初始化为 cur，避免后面的野指针问题。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1592025.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

Golang 开发实战day10 - Maps

Golang 开发实战day10 - Maps

&#x1f3c6;个人专栏 &#x1f93a; leetcode &#x1f9d7; Leetcode Prime &#x1f3c7; Golang20天教程 &#x1f6b4;‍♂️ Java问题收集园地 &#x1f334; 成长感悟 欢迎大家观看&#xff0c;不执着于追求顶峰&#xff0c;只享受探索过程 Golang 教程10 - Maps 1. M…
阅读更多...
WordPress网站上添加看板娘

WordPress网站上添加看板娘

续接上篇——基于LNMP部署wordpress-CSDN博客 目录 一.下载并解压 二.设置头文件 修改header.php 修改配置文件footer.php 三.将你设置的主题包上传到/usr/share/nginx/html/wp-content这个目录里 四.扩展——将看板娘修改到左侧 一.下载并解压 [rootaliyun ~]# wget htt…
阅读更多...
2024年阿里云优惠券领取，买前必看的多渠道代金券获取方法

2024年阿里云优惠券领取，买前必看的多渠道代金券获取方法

阿里云优惠代金券领取入口&#xff0c;阿里云服务器优惠代金券、域名代金券&#xff0c;在领券中心可以领取当前最新可用的满减代金券&#xff0c;阿里云百科aliyunbaike.com分享阿里云服务器代金券、领券中心、域名代金券领取、代金券查询及使用方法&#xff1a; 阿里云优惠券…
阅读更多...
Leetcode刷题之删除有序数组的重复项

Leetcode刷题之删除有序数组的重复项

一、题目描述 删除有序数组的重复项 给你一个 非严格递增排列 的数组 nums &#xff0c;请你 原地 删除重复出现的元素&#xff0c;使每个元素 只出现一次 &#xff0c;返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums…
阅读更多...
360安全卫士去除广告方法

360安全卫士去除广告方法

大安全时代&#xff0c;360 安全卫士为您提供全面安全服务&#xff0c;电脑端下载&#xff1a; https://urlqh.cn/orQqc 在当今数字化时代&#xff0c;网络安全已成为人们日常生活中的重要关切。在这片浩瀚的网络海洋中&#xff0c;360安全卫士犹如一座坚不可摧的灯塔&#xf…
阅读更多...
TL431内部架构学习

TL431内部架构学习

在V/I转换那个篇章里面看到了TL431的内部架构,那我们这一篇一点点的解析TL431的构成,首先TL431的内部详细原理图如下图1所示,为了便于理解我对管子进行了标注,倒时候我们好分析 图1:TL431内部原理图 拿到原理图后我们先简单的拆分,Q10和Q11就是达林顿管,控制Cathode的电压的Q2…
阅读更多...
【RHEL】redhat yum 报错: not registered to Red Hat Subscription Management.

【RHEL】redhat yum 报错: not registered to Red Hat Subscription Management.

【RHEL】redhat yum 报错: not registered to Red Hat Subscription Management. 问题描述解决方法参考博客&#xff1a; 问题描述 使用redhat7用yum install -y dos2unix命令时出现这个错误 This system is not registered to Red Hat Subscription Management. You can use …
阅读更多...
Zotero插件ZotCard中AI-NNDL文献笔记卡

Zotero插件ZotCard中AI-NNDL文献笔记卡

github&#xff1a;ZotCard插件AI-NNDL论文卡片模板 Issue #67 018/zotcard (github.com) ZotCard插件AI-NNDL论文卡片模板是关于人工智能神经网络与深度学习论文的笔记卡片&#xff0c;效果预览如下图&#xff1a; 经过了整理代码如下&#xff1a; <h1><span styl…
阅读更多...
Vue2 —— 学习（六）

Vue2 —— 学习（六）

一、Vue 脚手架 &#xff08;一&#xff09;介绍 Vue 脚手架是 Vue 官方提供的标准化开发工具 &#xff08;开发平台&#xff09; 脚手架版本最新版本 是 4.x 文档可以查看 http://cli.vuejs.org/zh/ 就是vue 官网文档中 的 vue.cli command line interface &#xff08;…
阅读更多...
最齐全，最简单的免费SSL证书获取方法——实现HTTPS访问

最齐全，最简单的免费SSL证书获取方法——实现HTTPS访问

一&#xff1a;阿里云 优势&#xff1a;大平台&#xff0c;在站长中知名度最高&#xff0c;提供20张免费单域名SSL证书 缺点&#xff1a;数量有限&#xff0c;并且只有单域名证书&#xff0c;通配符以及多域名没有免费版本。并且提供的单域名证书只有三个月的期限。 二&#…
阅读更多...
每日一题 第八十九期 洛谷 [NOIP2017 提高组] 奶酪

每日一题 第八十九期 洛谷 [NOIP2017 提高组] 奶酪

[NOIP2017 提高组] 奶酪 题目背景 NOIP2017 提高组 D2T1 题目描述 现有一块大奶酪&#xff0c;它的高度为 h h h&#xff0c;它的长度和宽度我们可以认为是无限大的&#xff0c;奶酪中间有许多半径相同的球形空洞。我们可以在这块奶酪中建立空间坐标系&#xff0c;在坐标系…
阅读更多...
10 Php学习：循环

10 Php学习：循环

在 PHP 中&#xff0c;提供了下列循环语句&#xff1a; while - 只要指定的条件成立&#xff0c;则循环执行代码块do…while - 首先执行一次代码块&#xff0c;然后在指定的条件成立时重复这个循环for - 循环执行代码块指定的次数foreach - 根据数组中每个元素来循环代码块 当…
阅读更多...
一款免费、开源、可批量识别的离线OCR软件，适用于 Windows7 x64及以上平台

一款免费、开源、可批量识别的离线OCR软件，适用于 Windows7 x64及以上平台

免费&#xff1a;本项目所有代码开源&#xff0c;完全免费。方便&#xff1a;解压即用&#xff0c;离线运行&#xff0c;无需网络。高效&#xff1a;自带高效率的离线OCR引擎&#xff0c;内置多种语言识别库。灵活&#xff1a;支持命令行、HTTP接口等外部调用方式。功能&#x…
阅读更多...
【cocos creator】【TS】贝塞尔曲线，地图之间显示曲线，顺着曲线移动

【cocos creator】【TS】贝塞尔曲线，地图之间显示曲线，顺着曲线移动

参考&#xff1a; https://blog.csdn.net/Ctrls_/article/details/108731313 https://blog.csdn.net/qq_28299311/article/details/104009804 const { ccclass, property } cc._decorator;ccclass export default class mapPanel extends cc.Component {property(cc.Node)pla…
阅读更多...
从零开始编写一个cmake构建脚本

从零开始编写一个cmake构建脚本

简介 本文档介绍cmake构建脚本编写&#xff0c;包含的一些主要元素和命名规范。 cmake构建脚本编写步骤 cmake构建工具版本要明确 # 命令名字要小写&#xff0c;这条语句要求构建工具至少需要版本为3.12或以上 cmake_minimum_required (VERSION 3.12)工程名及库的版本号明确…
阅读更多...
spring boot学习第十七篇:OAuth2概述及使用GitHub登录第三方网站

spring boot学习第十七篇:OAuth2概述及使用GitHub登录第三方网站

0. 导言 我们在浏览器上可以访问成百上千个网站&#xff0c;使用每个网站的服务一般都要先注册账号&#xff0c;那么我们为了更好地记忆&#xff0c;一般都会在多个网站使用相同的账号和密码进行注册。那么问题就来了&#xff0c;如果在你注册的网站中有某些个网站的系统设计不…
阅读更多...
C语言-----结构体详解

C语言-----结构体详解

前面已经向大家介绍过一点结构体的知识了&#xff0c;这次我们再来深度了解一下结构体。结构体是能够方便表示一个物体具有多种属性的一种结构。物体的属性可以转换为结构体中的变量。 1.结构体类型的声明 1.1 结构体的声明 struct tag {member-list;//结构体成员变量 }vari…
阅读更多...
VLC-Qt实现简单的视频播放器

VLC-Qt实现简单的视频播放器

VLC-Qt是一个结合了Qt应用程序和libVLC的免费开源库。它提供了用于媒体播放的核心类&#xff0c;以及用于快速开发媒体播放器的GUI类。由于集成了整个libVLC&#xff0c;VLC-Qt具备了libVLC的所有特性&#xff0c; 例如&#xff1a;libVLC实例和播放器、单个文件和列表播放、音…
阅读更多...
海山数据库（He3DB）原理剖析：浅析Doris跨源分析能力

海山数据库（He3DB）原理剖析：浅析Doris跨源分析能力

Doris湖仓分析背景&#xff1a; Doris多数据源功能演进 Doris的生态近年来围绕湖仓分析做了较多工作&#xff0c;Doris一直在积极拓宽大数据生态的OLAP分析市场&#xff0c;Doris2.0之后为了满足湖仓分析场景&#xff0c;围绕multi-catalog、数据缓存、容错、pipeline资源管理…
阅读更多...
LibRadtran使用教程

LibRadtran使用教程

LibRadtran使用教程 1.简介2.基本语法规则3.例子3.1 例子13.2 例子2 1.简介 关于LibRadtran的介绍以及安装可以参考另一篇博文&#xff1a;Windows系统LibRadtran安装。这里将针对LibRadtran的基础使用&#xff0c;以及基本语法进行介绍。 2.基本语法规则 uvspec < input…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023