题目分析

给定一组选用的数码管，要求判断这些数码管是否连通。连通的定义是：所有选用的数码管中的发光二极管必须构成一个连通的图，即从任意一个发光的二极管出发，可以到达其他所有发光的二极管。

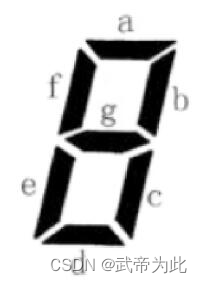
思路与算法

1. 构建数码管的邻接矩阵：由于七段码数码管中的二极管之间存在连接关系，可以用一个哈希表（unordered_map）来表示数码管的邻接关系。其中，键为每个二极管的标记，值为与之相邻的二极管的标记。
2. 使用DFS进行搜索：从选用的数码管中的第一个二极管开始，使用深度优先搜索算法遍历所有与之相邻的二极管，并标记为已访问。通过这种方式，我们可以检查所有发光的二极管是否构成了一个连通的图。
3. 检查连通性：遍历所有选用的数码管，如果有任何一个数码管未被访问到，则说明选用的数码管不连通；否则，选用的数码管是连通的。

代码

#include <iostream>
#include <vector>
#include <unordered_map>
#include <algorithm>

using namespace std;

string selection;  // 选用的数码管

// 定义七段码数码管的邻接关系
unordered_map<char, vector<char>> segments = {
    {'a', {'b', 'f'}},
    {'b', {'a', 'c', 'g'}},
    {'c', {'g', 'd', 'b'}},
    {'d', {'c', 'e'}},
    {'e', {'d', 'f', 'g'}},
    {'f', {'a', 'e', 'g'}},
    {'g', {'f', 'b', 'e', 'c'}}
};

// 深度优先搜索函数，用于检查数码管是否连通
void dfs(char node, unordered_map<char, bool>& visited) {
    visited[node] = true;
    for (char neighbor : segments[node]) {
        if (!visited[neighbor] && find(selection.begin(), selection.end(), neighbor) != selection.end()) {
            dfs(neighbor, visited);
        }
    }
}

int main() {
    cin >> selection;

    unordered_map<char, bool> visited; // 记录数码管是否被访问过
    // 初始化visited
    for (char segment : selection) {
        visited[segment] = false;
    }

    // 从第一个选用的数码管开始进行深度优先搜索
    dfs(selection[0], visited);

    // 检查是否所有选用的数码管都连通
    bool connected = true;
    for (char segment : selection) {
        if (!visited[segment]) {
            connected = false;
            break;
        }
    }

    if (connected) {
        cout << "yes" << endl;
    } else {
        cout << "no" << endl;
    }

    return 0;
}