LeetCode-416. 分割等和子集【数组 动态规划】
- 题目描述:
- 解题思路一:01背包问题,动规五部曲
- 解题思路二:0
- 解题思路三:0
题目描述:
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
示例 1:
输入:nums = [1,5,11,5]
输出:true
解释:数组可以分割成 [1, 5, 5] 和 [11] 。
示例 2:
输入:nums = [1,2,3,5]
输出:false
解释:数组不能分割成两个元素和相等的子集。
提示:
1 <= nums.length <= 200
1 <= nums[i] <= 100
解题思路一:01背包问题,动规五部曲
- 确定dp数组以及下标的含义
01背包中,dp[j] 表示: 容量为j的背包,所背的物品价值最大可以为dp[j]。
本题中每一个元素的数值既是重量,也是价值。
套到本题,dp[j]表示 背包总容量(所能装的总重量)是j,放进物品后,背的最大重量为dp[j]。
那么如果背包容量为target, dp[target]就是装满 背包之后的重量,所以 当 dp[target] == target 的时候,背包就装满了。
有录友可能想,那还有装不满的时候?
拿输入数组 [1, 5, 11, 5],举例, dp[7] 只能等于 6,因为 只能放进 1 和 5。
而dp[6] 就可以等于6了,放进1 和 5,那么dp[6] == 6,说明背包装满了。
- 确定递推公式
01背包的递推公式为:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
本题,相当于背包里放入数值,那么物品i的重量是nums[i],其价值也是nums[i]。
所以递推公式:dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);
- dp数组如何初始化
在01背包,一维dp如何初始化,已经讲过,
从dp[j]的定义来看,首先dp[0]一定是0。
如果题目给的价值都是正整数那么非0下标都初始化为0就可以了,如果题目给的价值有负数,那么非0下标就要初始化为负无穷。
这样才能让dp数组在递推的过程中取得最大的价值,而不是被初始值覆盖了。
本题题目中 只包含正整数的非空数组,所以非0下标的元素初始化为0就可以了。
-
确定遍历顺序
在动态规划:关于01背包问题,你该了解这些!(滚动数组) (opens new window)中就已经说明:如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环放在内层,且内层for循环倒序遍历! -
举例推导dp数组
dp[j]的数值一定是小于等于j的。
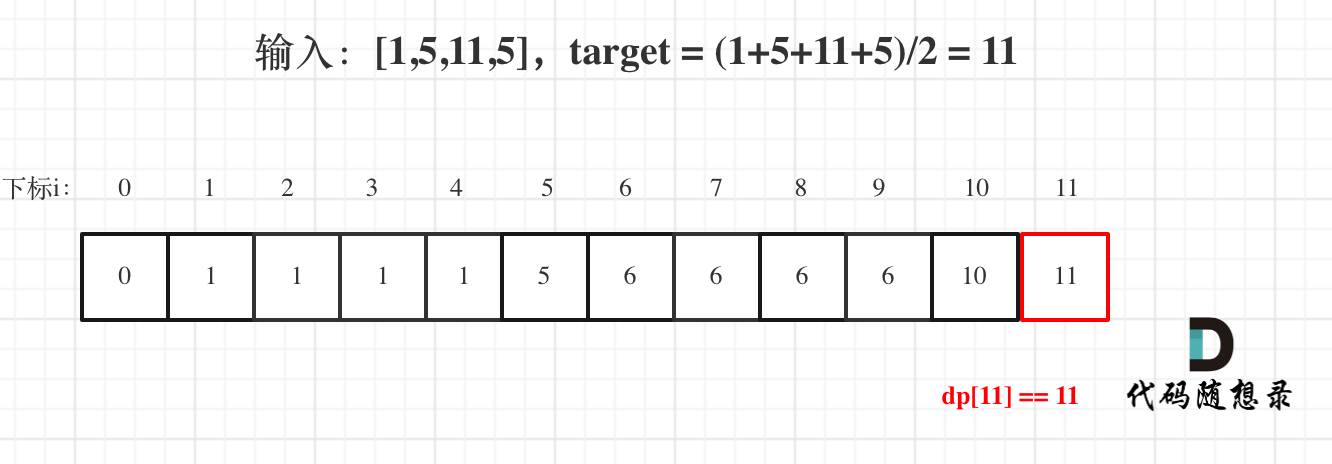
如果dp[j] == j 说明,集合中的子集总和正好可以凑成总和j,理解这一点很重要。
用例1,输入[1,5,11,5] 为例,如图:
class Solution:
def canPartition(self, nums: List[int]) -> bool:
if sum(nums) % 2 == 1:
return False
target = sum(nums) // 2
dp = [0] * (target + 1)
for num in nums:
for j in range(target, num - 1, -1):
dp[j] = max(dp[j], dp[j-num] + num)
return dp[target] == target
时间复杂度:O(n2)
空间复杂度:O(n)
解题思路二:0
时间复杂度:O(n)
空间复杂度:O(n)
解题思路三:0
时间复杂度:O(n)
空间复杂度:O(n)