文章目录
- 题目
- 303、区域和检索(数组不可变)
- 304、二维区域和检索(矩阵不可变)
- 解
- ①303,一维前缀和
- ②304,二维前缀和
- 算法
- 前缀和
- 一维前缀和
- 二维前缀和
题目
303、区域和检索(数组不可变)
给定一个整数数组 nums,处理以下类型的多个查询:
- 计算索引
left和right(包含left和right)之间的nums元素的 和 ,其中left <= right
实现 NumArray 类:
NumArray(int[] nums)使用数组nums初始化对象int sumRange(int i, int j)返回数组nums中索引left和right之间的元素的 总和 ,包含left和right两点(也就是nums[left] + nums[left + 1] + ... + nums[right])
示例 1:
输入:
["NumArray", "sumRange", "sumRange", "sumRange"]
[[[-2, 0, 3, -5, 2, -1]], [0, 2], [2, 5], [0, 5]]
输出:
[null, 1, -1, -3]
解释:
NumArray numArray = new NumArray([-2, 0, 3, -5, 2, -1]);
numArray.sumRange(0, 2); // return 1 ((-2) + 0 + 3)
numArray.sumRange(2, 5); // return -1 (3 + (-5) + 2 + (-1))
numArray.sumRange(0, 5); // return -3 ((-2) + 0 + 3 + (-5) + 2 + (-1))
304、二维区域和检索(矩阵不可变)
给定一个二维矩阵 matrix,以下类型的多个请求:
- 计算其子矩形范围内元素的总和,该子矩阵的 左上角 为
(row1, col1),右下角 为(row2, col2)。
实现 NumMatrix 类:
NumMatrix(int[][] matrix)给定整数矩阵matrix进行初始化int sumRegion(int row1, int col1, int row2, int col2)返回 左上角(row1, col1)、右下角(row2, col2)所描述的子矩阵的元素 总和 。
示例 1:

输入:
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出:
[null, 8, 11, 12]
解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]);
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)
解
①303,一维前缀和
class Solution {
public int[] productExceptSelf(int[] nums) {
int len=nums.length;
int[] answer=new int[len];
answer[0]=1;
for(int i=1;i<len;i++){
answer[i]=nums[i-1]*answer[i-1];
}
int R=nums[len-1]; // R存储右侧所有元素乘积
for (int i = len - 2; i >= 0; i--) {
answer[i] = answer[i] * R;
R=R*nums[i];
}
return answer;
}
}
②304,二维前缀和
class NumMatrix {
int[][] sum;
public NumMatrix(int[][] matrix) {
int m=matrix.length,n=matrix[0].length;
sum=new int[m+1][n+1];
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
sum[i][j]=sum[i-1][j]+sum[i][j-1]-sum[i-1][j-1]+matrix[i-1][j-1];
}
}
}
public int sumRegion(int row1, int col1, int row2, int col2) {
return sum[row2+1][col2+1]-sum[row1][col2+1]-sum[row2+1][col1]+sum[row1][col1];
}
}
算法
前缀和
前缀和是一种常见的算法技巧,用于快速计算数组中某个区间内元素的和,通常用于优化处理大量的区间求和问题,比如给定一个数组,询问其中某个连续区间内元素的和。
算法原理: 前缀和的核心思想是通过对数组进行预处理,计算出从数组开头到每个位置的元素累加和,然后利用这些预先计算好的累加和,在O(1)时间内求出任意区间的和。假设给定数组为A,其前缀和数组为prefix,其中prefix[i]表示数组A从0到i的元素和。
一维前缀和
假设给定数组为A = [1, 2, 3, 4, 5],其前缀和数组为prefix = [1, 3, 6, 10, 15]。
但在①②中,A数组的前缀和应当为prefix = [0,1, 3, 6, 10, 15],比原数组要多一个。
在计算任意区间的和时,通过在前缀和数组中添加0,可以统一处理起始位置为0的边界情况,无需单独考虑。例如,对于查询区间[0, 3],直接使用prefix[3]即可得到结果,无需特殊处理。
具体使用的时候建议用草稿纸绘制相关的数组或者矩阵的图形,进行检验。
二维前缀和
二维的前缀和更为复杂,
A = [ [1, 2, 3], [4, 5, 6], [7, 8, 9] ]
prefix = [ [1, 3, 6], [5, 12, 21], [12, 27, 45] ]
prefix[i] [j] = A[i] [j] + prefix[i-1] [j] + prefix[i] [j-1] - prefix[i-1] [j-1]
可以用下图帮助理解(图源LeetCode:负雪明烛):
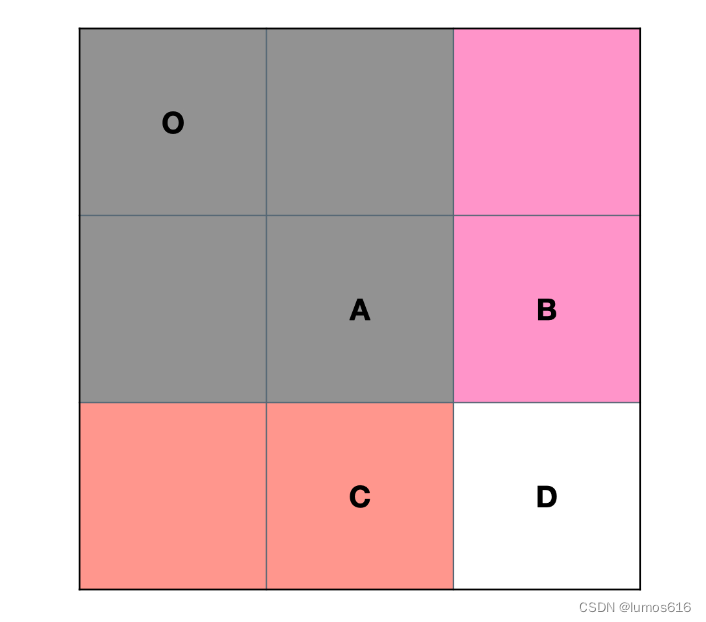
至于输出的公式,也类似于上面的用右下角位置加上左上角-1的位置减去区域右上角和左下角:
area=sum[row2+1] [col2+1]-sum[row1] [col2+1]-sum[row2+1] [col1]+sum[row1] [col1](为了方便书写代码,实际矩阵比原矩阵大一圈,所以这里所有的加减都在原矩阵基础上+1)