刷题之动态规划-两个数组

前言

大家好，我是jiantaoyab，开始刷动态规划的两个数组类型相关的题目

动态规划5个步骤

状态表示：dp数组中每一个下标对应值的含义是什么>dp[i]表示什么
状态转移方程： dp[i] 等于什么
1 和 2 是动态规划的核心步骤，第三步是初始化，保证填表的时候不越界
填表顺序：为了保证填写当前状态的时候，所需要的状态已经计算过
返回值

最长公共子序列

题目分析

代码

class Solution {
public:
    int longestCommonSubsequence(string text1, string text2) {
      int m = text1.size(), n = text2.size();
      //增加一行和一列 dp[i - 1][j - 1]的时候不会越界
      vector<vector<int>> dp(m + 1, vector<int>(n + 1));

      //初始化
      text1 = " " + text1, text2 = " " + text2;
      for(int i = 1; i <= m; i++)
      {
        for(int j = 1; j <= n; j++)
        { 
          if(text1[i] == text2[j]) dp[i][j] = dp[i - 1][j - 1] + 1;
          else
          dp[i][j] = max(dp[i][j - 1], dp[i - 1][j]);
        }
      }

      return dp[m][n];
    }
};

最长重复子数组

代码

class Solution {
public:
    int findLength(vector<int>& nums1, vector<int>& nums2) {
      int m = nums1.size(), n = nums2.size();
      vector<vector<int>> dp (m + 1, vector<int>(n + 1));
      int ret = 0;
        for(int i = 1; i <= m; i++)
        {
          for(int j = 1; j <= n; j++)
          {
            if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1 , ret = max(dp[i][j], ret);
            else
            {
              dp[i][j] = 0;
            }
          }
        }
        return ret;
    }
};

不相交的线

代码

这道题目和上一道题目很像，不过是在数组中最长公共的子序列

class Solution {
public:
    int maxUncrossedLines(vector<int>& nums1, vector<int>& nums2) {
        int m = nums1.size(), n = nums2.size();
        //避免dp[i - 1][j - 1]越界
        vector<vector<int>> dp (m + 1, vector<int>(n + 1));
        for(int i = 1; i <= m; i++)
        {
          for(int j = 1; j <= n; j++)
          {
            if(nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;
            else
            {
              dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);
            }
          }
        }
        return dp[m][n];
    }
};

不同的子序列

题目分析

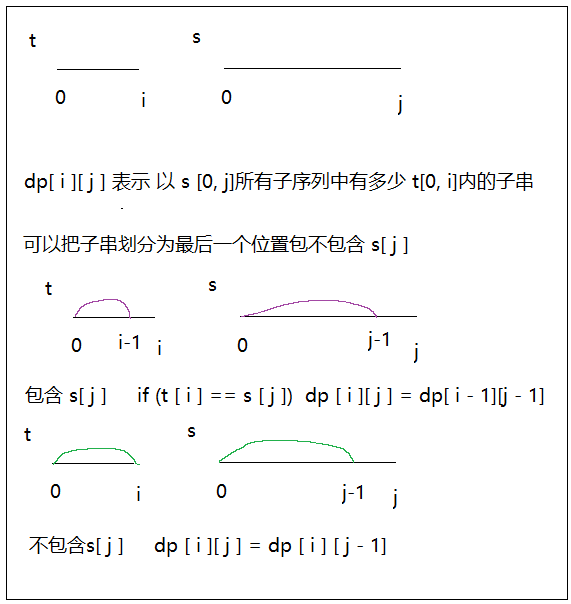
代码

class Solution {
public:
    int numDistinct(string s, string t) {
        int m = t.size(), n = s.size();

        vector<vector<int>> dp(m + 1, vector<int>(n + 1));

        for(int j = 0; j <= n; j++) dp[0][j] = 1; //初始化

        for(int i = 1; i <= m; i++)
        {
          for(int j = 1; j <= n; j++)
          {
            dp[i][j] += dp[i][j - 1];
            if(t[i - 1] == s[j - 1]) dp[i][j] += dp[i - 1][j - 1] % 10000000007; 
                            
          }
        }
        return dp[m][n];
    }
};

通配符匹配

题目分析

初始化

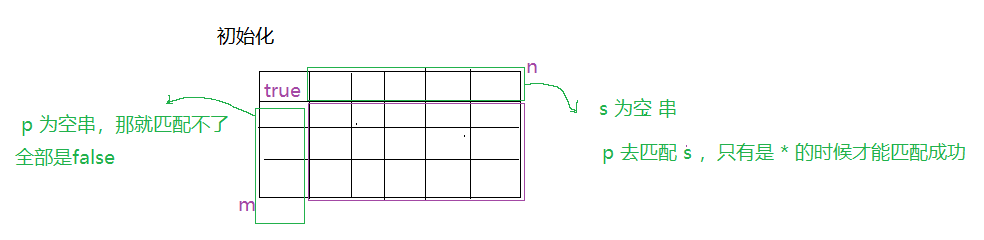
代码

class Solution {
public:
    bool isMatch(string s, string p) {
      int m = s.size(), n = p.size();
      vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
      s= " " + s, p = " " + p;
      //初始化
      dp[0][0] = true; //空串匹配空串
      for(int j = 1; j <= n; j++) 
      {
        if(p[j] == '*') dp[0][j] = true;
        else break;
      }
      for(int i = 1; i <= m; i++)
      {
        for(int j = 1; j <= n; j++)
        {
          if(p[j] == s[i] && dp[i -1][j - 1] == true) dp[i][j] = true;
          else if(p[j] == '?' &&  dp[i - 1][j- 1] == true) dp[i][j] = true;
          else if(p[j] == '*') dp[i][j] = dp[i - 1][j] || dp[i][j - 1];
       
        }
      }
      return dp[m][n];

    }
};

正则表达式匹配

题目分析

这里的*是根据前面的字符来匹配的，不能单独使用。

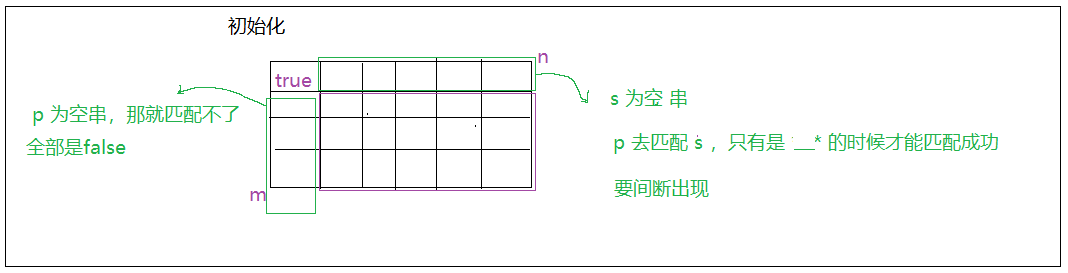
代码

class Solution {
public:
    bool isMatch(string s, string p) {
      int m = s.size(), n = p.size();
      vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
      //初始化
      dp[0][0] = true;
      s = ' ' + s , p = ' ' + p;
      for(int j = 2; j <= n; j += 2)
      {
        if(p[j] == '*') dp[0][j] = true;
        else break;
      }

      for(int i = 1; i <= m; i++)
      {
        for(int j = 1; j <= n; j++)
        {
          if( p[j] == '*')
           dp[i][j] = dp[i][j - 2] || (p[j - 1] == '.' || p[j - 1] == s[i]) && dp[i -1][j];    
          else         
           dp[i][j] = (s[i] == p[j] || p[j] == '.') && dp[i - 1][j - 1] ;

     
        }
      }
      return dp[m][n];
    }
};

交错字符串

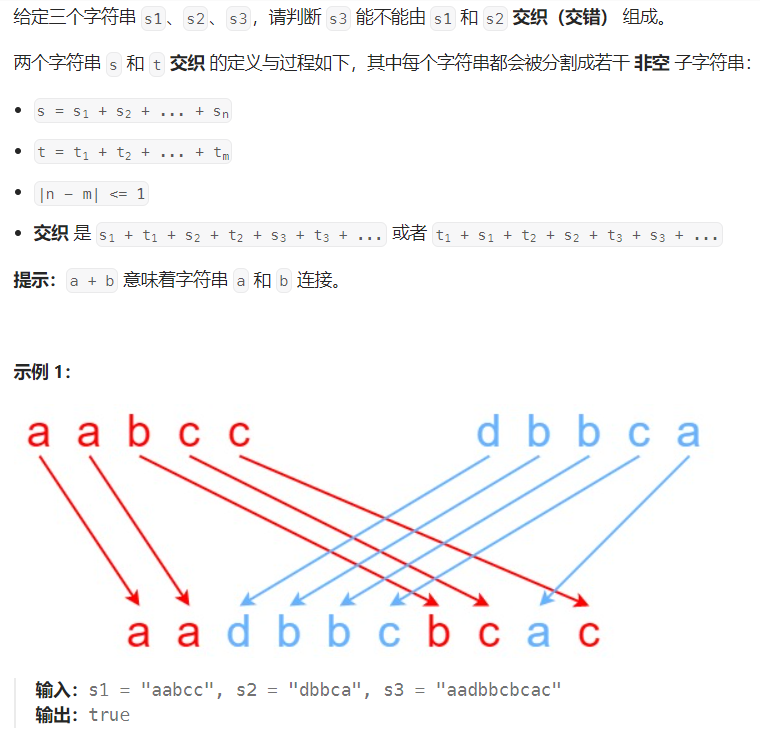
题目分析

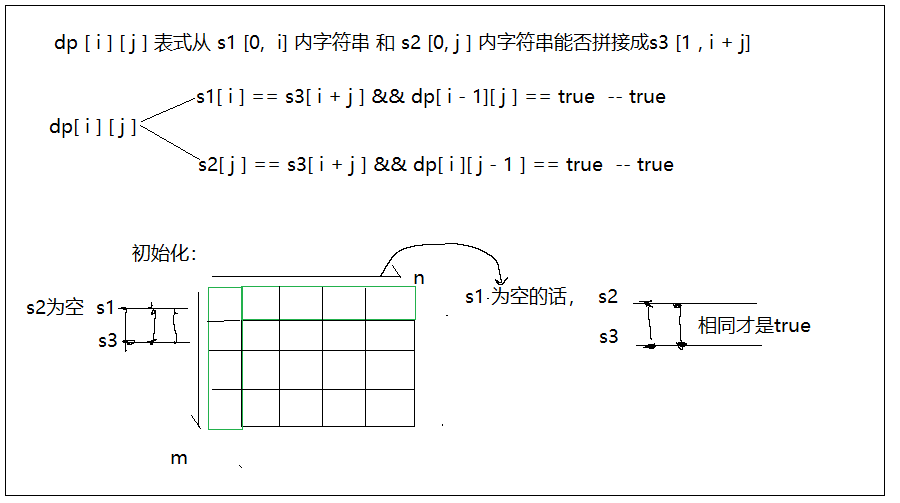
代码

class Solution {
public:
    bool isInterleave(string s1, string s2, string s3) {
      int m = s1.size(), n = s2.size();
      if(n + m != s3.size()) return false;
       vector<vector<bool>> dp(m + 1, vector<bool>(n + 1));
      s1 = " " + s1, s2 = " " + s2, s3 = " " + s3;
      //初始化
      dp[0][0] = true;
      for(int i = 1; i <= n; i++) 
        if(s2[i] == s3[i]) dp[0][i] = true;
        else break;
      for(int j = 1; j <= m; j++) 
        if(s1[j] == s3[j]) dp[j][0] = true;
        else break;
      
      for(int i = 1; i <= m; i++)
      {
        for(int j = 1; j <= n; j++)
        {
          if(s1[i] == s3[i + j] && dp[i - 1][j]) dp[i][j] = true;
          else if(s2[j] == s3[i + j] && dp[i][j - 1]) dp[i][j] = true;
        }
      }
      return dp[m][n];
    }
};

两个字符串的最小ASCII删除和

代码

class Solution {
public:
    int minimumDeleteSum(string s1, string s2) {
      int m = s1.size(), n = s2.size();
      //dp[i][j] 表示s1[0, i]和s2[0, j]公共子串ascii值最大
      vector<vector<int>> dp (m + 1, vector<int>(n + 1));
      
      for(int i = 1; i <= m; i++)
      {
        for(int j = 1; j <= n; j++)
        {
          dp[i][j]  = max(dp[i][j - 1], dp[i - 1][j]);
          if(s1[i - 1] == s2[j - 1]) 
          dp[i][j] = max(dp[i][j], dp[i - 1][j - 1] + s1[i - 1]);       
        }
      } 
      int sum = 0;
      for(auto c : s1) sum += c;
      for(auto c : s2) sum += c;
      return sum - dp[m][n] - dp[m][n];
    }
};