sprintf函数源自 C 语言标准库中的同名函数,这个函数在 C 语言中用于创建格式化的字符串,且使用频率非常高。作为一门高级编程语言,MATLAB借鉴了 C 语言和其他编程语言中的许多特性和命名惯例。在MATLAB中,sprintf函数主要有两种用法:解析转义字符和执行格式化文本操作,下面我们分别介绍这两种用法。
基础用法:解析转义字符
上一章讲解strjoin函数时,我们介绍过转义字符的概念。转义字符是一类特殊的字符,用于在文本中表示无法直接输入的特定字符。例如,转义字符\n表示换行符、\t表示水平制表符、\r表示回车符等。
在MATLAB中,sprintf函数可以解析文本中的转义字符,即将它们转换为相应的特定字符。下面我们直接引用MATLAB的官方文档来介绍这种用法:
str = sprintf(literalText) 转换literalText 中的转义字符序列,例如 \n 和 \t。它会原样返回所有其他字符。literalText指定为字符向量或字符串标量。
这种用法简单直接,下面来看两个具体的例子:

此外,官方文档中还有额外补充的一句话:如果输入参数表示的文本中包含格式化操作符,则输出的结果中将丢弃该字符以及之后的所有字符。这句话中出现了一个新的概念:格式化操作符,我们会在下面的高级用法中给大家介绍。
高级用法:格式化文本操作
sprintf函数的高级用法用于将数据按照特定的格式转换为文本。这种格式化操作可以让我们以非常具体的方式控制文本的呈现,包括数字的精度、对齐方式、字段宽度等。在生成报告、展示数据等场景中,这种功能显得尤为重要,因为它能够确保信息的准确性和一致性,同时使文本输出更加整洁和易读。
我们先引用MATLAB 的官方文档来介绍sprintf函数用于格式化文本的方法:
str = sprintf(formatSpec,A1,...,An) 使用 formatSpec 指定的格式化操作符格式化数组 A1,...,An 中的数据,并在 str 中返回结果文本。sprintf 函数按列顺序格式化 A1,...,An 中的值。如果 formatSpec 是字符串,则输出 str 也是字符串;否则,str 是字符向量。(注:所谓的格式化,可以理解为用A1,...,An替换formatSpec中的格式化操作符)
在此用法中,formatSpec是一个核心参数,代表输出文本的格式。它可以包含格式化操作符、普通文本和特殊字符(如转义字符),其数据类型为字符向量或字符串标量。而A1, ..., An则是一组用于格式化的数值、字符或字符串数组,可以有一个或多个。
上方介绍中出现了一个重要的概念:格式化操作符。格式化操作符是该函数的核心,它以百分号%开头,且必须以转换字符结束。在这两者之间,我们还可以指定标识符、标志、字段宽度、精度和子类型,这些都是可选参数。
MATLAB官网上有一个最完整的格式化操作符的例子:'%3$0-12.4bu',其分解如下:

上面展示的格式化操作符的例子虽然全面,但对于初学者而言可能过于复杂,且在实际应用中使用的频率并不高。因此,在本书中,我们将专注于那些更常用且易于理解的格式化操作符的用法。这样做的目的是为了使知识点更加贴近实际应用,同时也便于大家快速掌握MATLAB中文本格式化的核心技巧。
另外,在上述介绍中,我们提到了格式化操作符的多个组成部分。为了更深入地理解这些部分的作用,我们将分别介绍它们各自的功能和用法。
一、转换字符(格式化操作符必须以转换字符结束)
下面我们介绍几种最常用的转换字符:d或i、f、e和s。这五个转换字符在文本格式化的应用中最为常见,掌握它们的用法能够满足大多数的格式化文本需求。
(1)d或i:这两个转换字符用于格式化整数

(2)转换字符f:以定点记数法格式化数据

从上面的例子可以看出,直接使用'%f'会保留小数点后6位。如果需要自己控制保留的小数点位数,需要结合可选的“精度”参数一同使用。例如保留三位小数的格式化操作符为'%.3f',保留五位小数的格式化操作符为'%.5f',我们在后面会具体介绍。
(3)转换字符e:以科学记数法格式化数据

从结果可以看出,使用'%e'表示为科学计数法时,MATLAB默认也会保留小数点后6位,我们也可以结合可选的“精度”参数一同使用,后面会给大家展示例子。
(4)转换字符s:格式化文本数据

以上就是几个使用频率很高的转换字符的介绍。大家可以查看sprintf函数的帮助文档,帮助文档中有更多转换字符如u、o、x、g、c等的介绍,它们使用频率较低。
下面给大家额外补充三个知识点,来帮助大家更好地理解sprintf函数的用法:
知识点一:错误的格式化操作符
在使用sprintf函数时,选择正确的格式化操作符至关重要。错误的格式化操作符会导致输出的结果不符合预期。例如,'%p'并不是一个标准的MATLAB格式化操作符,使用它会导致文本的后续部分被意外丢弃。

事实上,sprintf函数可以有第二个返回值,用法如下:如果操作失败,[str,errmsg] = sprintf(formatSpec,A1,...,An) 将以字符向量形式返回一条错误消息。否则,errmsg 为空。

知识点二:多元素数组的处理
在上面展示的示例中,我们主要关注了如何使用 sprintf 函数格式化单个数值或文本。然而,根据 MATLAB 官方文档中的描述:str = sprintf(formatSpec, A1, ..., An) 使用 formatSpec 指定的格式化操作符对数组 A1, ..., An 中的数据进行格式化。这意味着 A1, ..., An 可以是具有多个元素的向量或矩阵。当我们使用向量或矩阵作为函数的输入时,sprintf 函数会按照线性索引的顺序来格式化。让我们通过两个简单的例子来理解这一点:

下面我们再来看两个更为复杂的例子,当formatSpec参数中包含多个格式化操作符时,MATLAB会依次使用数组参数中的元素进行替换。

知识点三:特殊的字符
使用sprintf函数时,对特殊字符的正确处理至关重要。以下是处理一些常见特殊字符的例子:

二、精度(可选项)
精度是格式化操作符中的一个核心可选项,用于控制数字在格式化为文本时的精确程度。它主要用于 %f(定点记数法)和%e(科学记数法),可用来控制小数点右侧的位数。
例如:%.nf和%.ne格式化操作符可以指定小数点后保留n位数字。我们举几个例子:

尽管设置精度看似是一个简单的任务,但它在数据呈现中扮演着至关重要的角色。
在实际应用中,适当的精度设置有助于确保数据的准确传达,避免可能的误解或数据丢失。例如,在财务报告中,过多的小数位可能会导致读者阅读困难;而在科学研究中,小数位的减少可能会影响结果的准确性。因此,理解并正确设置精度是数据处理和展示的一个关键技能。
三、字段宽度(可选项)
字段宽度是格式化操作符中的一个重要可选项,用于控制文本输出的布局。具体来说,它定义了每个格式化字段应占用的最小字符数量。在sprintf函数中,字段宽度通过一个数字指定,该数字位于百分号%和精度选项之间(如果存在精度选项的话)。
如果实际值的字符数量少于指定的字段宽度,则MATLAB会使用空格在左侧填充余下的空间。这种填充保证了每个字段至少占用指定宽度的空间,从而使输出的文本在视觉上更加统一和整齐。
下面我们来看几个指定字段宽度的例子:
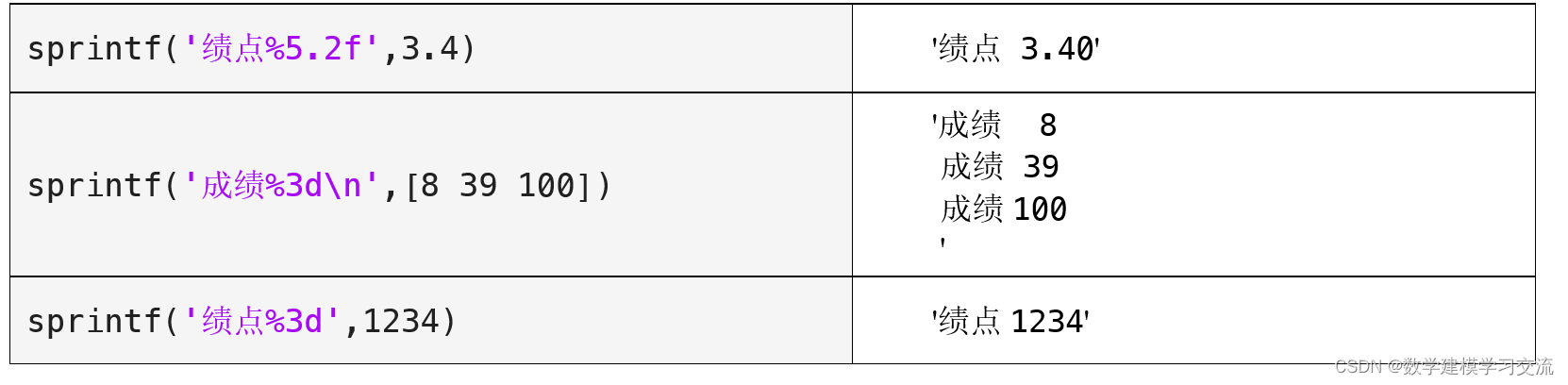
前两个例子比较容易理解,最后一个例子比较特殊:在这个例子中,字段宽度被设置为3,而实际数值1234占据了4个字符的位置。在这种情况下,sprintf函数不会截断或省略实际数值,而是保留完整的数值。字段宽度的作用主要是确保文本至少占用设定宽度的空间,如果实际数值超出了这个宽度,它会完整地显示出来。
这样的格式化使得即使在数值长度不一致的情况下,输出的文本也能保持整齐,从而大幅提升了信息的可读性和专业感。例如,在制作成绩表格或财务报告时,利用字段宽度确保所有数据列对齐,就能让整个文档看起来更加清晰、有序。
四、标志(可选项)
在格式化操作符中,标志是用来进一步调整输出文本布局的可选项。通过使用不同的标志,我们可以控制数值和文本的对齐方式、符号显示等。
使用时,标志参数需要放在百分号%和字段宽度之间(如果存在字段宽度的话)。下面我们介绍三种常见的标志及其使用方式:
(1)'-' :左对齐标志(实际上就是键盘上的减号)
标志'-'确保文本或数值在指定的字段宽度内靠左对齐,剩余的字符使用空格填充。

(2)'+' :始终显示符号(实际上就是键盘上的加号)
标志'+'用于确保无论正数还是负数,数值前面都会显示一个符号(+或-)。这在需要明确区分正负值时非常有用。

此外,我们可以同时设置多个标志,且标志出现的顺序对结果没有影响。例如:

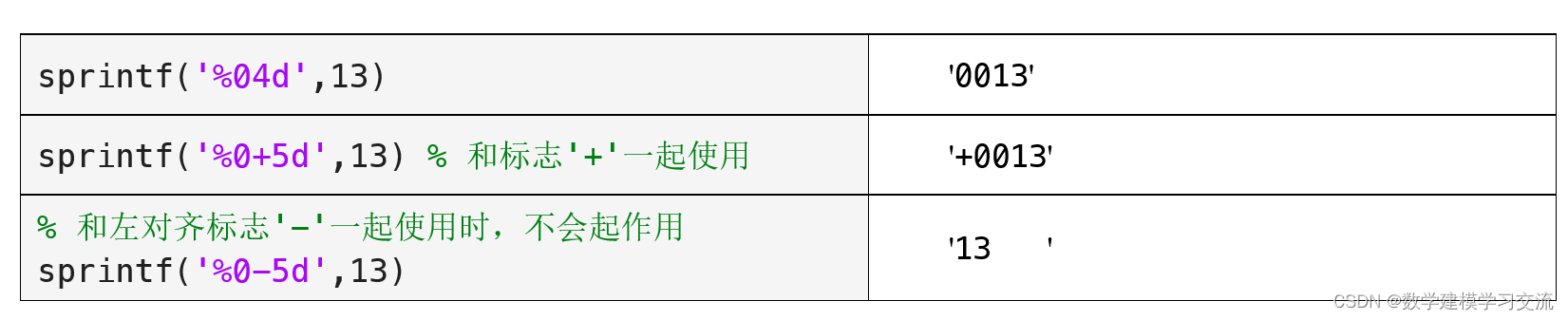
(3)'0':在值之前补零以填充字段宽度
在默认情况下,MATLAB使用空格来填充并达到指定的字段宽度。然而,使用'0'标志可以让我们用数字0来进行填充。
五、标识符(可选项、很少用到)
标识符是格式化操作符中的一个高级功能,用于指定函数输入参数的顺序。虽然在日常使用中不太常见,但在某些特定场合,它可以提供额外的灵活性,尤其是在需要调整输出顺序或重复使用某些参数时。
在sprintf函数中,标识符通过'n$'的形式来实现,其中'n'代表了其他输入参数在函数调用中的位置。这种方式允许我们在格式化文本时重新排列或重复使用参数,而不必改变输入参数的实际顺序。
使用时,标识符参数需要放在百分号%和标志之间(如果存在标志的话)。下面我们来看两个例子:

需要注意的是,如果输入参数是一个包含多个元素的数组,则标识符不能用来指定数组中的元素顺序,大家可以自己尝试。
六、子类型(可选项、极少用到)
子类型是格式化操作符中的一个高度专业化的功能,它主要用于将浮点数以不同精度的数制(如八进制、十进制、十六进制)进行展示。子类型紧邻转换字符之前,位于其他可选参数之后。下面我们看一个具体的例子来理解其用法:

在这个例子中,'b' 表示双精度的子类型,而 'x' 是表示十六进制的转换字符。它们结合在一起用于将圆周率π转换为其双精度十六进制的表示形式。这种表示并非用于日常的数值阅读,而是为了满足底层的编程调试或特定的科学计算需求,例如处理硬件驱动、嵌入式编程、操作系统底层调试等。
除了上述示例,sprintf函数还提供了其他子类型的表示方法(大家有印象即可,不需要刻意去记):
'%bo':将浮点数表示为双精度八进制;'%bu':将浮点数表示为双精度十进制;'%tx'将浮点数表示为单精度十六进制;'%to':将浮点数表示为单精度八进制;'%tu':将浮点数表示为单精度十进制。
介绍完sprintf函数的使用方法后,接下来我们通过两个例题帮助大家更好地掌握它在实际编程中的应用。
例题1:构造所有可能的生日
在某些应用场景中,我们可能需要构造一个包含所有可能生日的列表。例如,在统计分析或数据模拟中,可能需要对每一日的数据进行处理。本例演示如何使用MATLAB构造包含所有可能生日的字符串数组(考虑闰年,共366天)。每个生日都按照"mmdd"的格式构造,确保月份和日期部分均是两位数。例如,"0115"表示1月15日,"0803"表示8月3日。(本题节选自上一章课后习题的提高篇Q7)

在这段代码中,我们首先定义了月份和每个月的天数;接下来,我们使用双层循环遍历每个月的每一天,并使用sprintf函数来格式化每个日期为"mmdd"格式,格式化后的日期被储存在字符串数组S中;最后,我们输出S,此时S中保存着按照日期顺序排列的所有生日。
例题2:输出二分搜索法的中间计算结果
本题改编自第四章4.2.3节的例题,原题如下图所示:

通过上面这个例题,我们详细探讨了二分搜索法的原理和实现方法,验证了这种方法在求解函数零点问题上的有效性和高效性。二分搜索法的实质是不断缩小搜索区间,逐步逼近目标值,直到达到预设的精度要求。然而,在实际编程实现过程中,我们不仅需要关心算法的最终结果,更需要关注算法的执行过程,特别是在调试阶段或者分析算法性能时。为此,实时监控算法的执行细节就显得尤为重要。
在二分搜索法的实现中,我们通常关注以下几个关键信息:
迭代次数:显示当前是第几次迭代,帮助我们了解算法收敛的速度。
当前区间:展示当前的搜索区间,让我们知道零点可能的所在范围。
区间中点:即当前迭代的零点估计值,是算法逼近真实零点的媒介。
函数值:中点处的函数值,用于判断是否已接近零点。
借助sprintf函数,我们可以按照特定的格式来组织这些信息,使输出内容既丰富美观又易于理解。
a = 6; b = 10; % 设置初始搜索区间
epsilon = 1e-8; % 设置误差阈值
iter = 1; % 迭代次数
while 1 % 开始二分搜索
c = (a + b) / 2; % 计算区间中点
fc = c^3 - 8*c^2 + c - 5; % 计算中点处的函数值
cc = '迭代次数: %2d, 当前区间: [%.6f, %9.6f], 区间中点: %.6f, 函数值: %12.8f';
s = sprintf(cc, iter, a, b, c, fc);
disp(s) % 输出当前迭代的详细信息
if abs(fc) < epsilon % 如果中点处的函数值已经足够接近零,停止搜索
break
end
fa = a^3 - 8*a^2 + a - 5; % 否则根据函数值的正负来调整搜索区间
if fa * fc < 0 % f(a) × f(c)<0
b = c; % 区间更换为[a,c]
else % f(c) × f(b)<0
a = c; % 区间更换为[c,b]
end
iter = iter + 1;
end

点击下方的CSDN专栏阅读下一篇文章:
MATLAB入门课程专栏