C++学习笔记---014
- C++之queue的应用及模拟实现
- 1、queue的简单介绍
- 2、queue的简单接口应用
- 3、queue的模拟实现
- 3.1、queue的结构一般的构建
- 3.2、queue的适配器模式构建
- 3.3、queue的主要接口函数
- 4、queue的模拟实现完整代码
- 4.1、一般方式
- 4.2、泛型模式
- 5、queue巩固练习题
- 5.1、最小栈
- 5.2、栈的匹配(栈的压入和弹出序列)
- 5.3、逆波兰表达式求值 (后缀表达式)
- 5.4、两个栈实现队列
C++之queue的应用及模拟实现
前言:
前面篇章学习了C++对于stack容器的基本使用以及常用接口的认识,接下来继续学习,C++的queue的模拟实现等知识。
/知识点汇总/
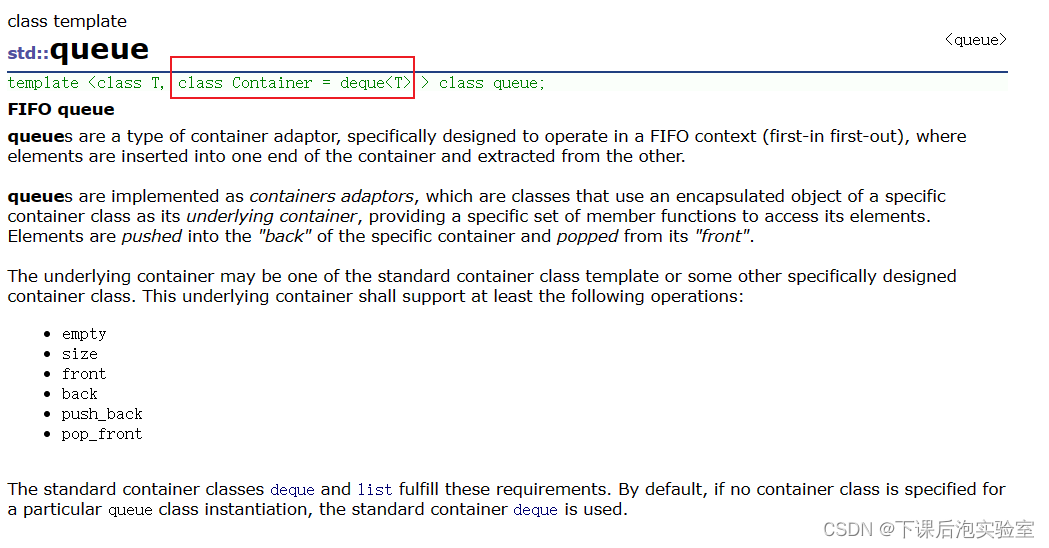
1、queue的简单介绍
在C++中,queue是一种基于先进先出(FIFO)原则操作的容器。
与日常生活中的排队类似,队列的头部是第一个被添加的元素,也是第一个可以被删除的元素。
新添加的元素总是被放在队列的尾部。
queue为这种数据结构提供了一组函数来操作和访问元素。
以下是queue的一些基本特性和操作:
1.基本特性:
先进先出(FIFO):队列的头部是第一个被添加的元素,也是第一个可以被删除的元素。新添加的元素总是被放在队列的尾部。
动态性:queue的大小是动态的,可以根据需要自动增长或缩小。
不支持随机访问:queue不支持通过索引直接访问任意位置的元素,只能从队头开始依次访问。
容器的通用性:queue可以容纳任何类型的元素,包括基本类型和自定义类型。
2.常用操作:
front():返回queue中第一个元素的引用。如果queue是常量,就返回一个常引用;如果queue为空,返回值是未定义的。
back():返回queue中最后一个元素的引用。如果queue是常量,就返回一个常引用;如果queue为空,返回值是未定义的。
push(const T& obj):在queue的尾部添加一个元素的副本。这是通过调用底层容器的成员函数push_back()来完成的。
push(T&& obj):以移动的方式在queue的尾部添加元素。这是通过调用底层容器的具有右值引用参数的成员函数push_back()来完成的。
pop():移除queue头部的元素。注意,这个操作不返回被移除的元素,也不检查queue是否为空。在调用pop()之前,应确保queue不为空,否则可能会导致未定义行为。
empty():检查queue是否为空。如果为空,返回true;否则返回false。
size():返回queue中元素的数量。
3.需要注意的是:
queue的内部实现使用了底层容器来存储元素,并且只能通过特定的函数来访问和操作元素。默认情况下(官方),底层容器的类型是deque,但也可以使用其他容器类型,如list。
总的来说,C++中的queue是一个简单但非常实用的数据结构,用于处理那些需要按照特定顺序(即先进先出)访问和操作元素的场景。
2、queue的简单接口应用
void test_queue()
{
queue<int> qt;
qt.push(1);
qt.push(2);
qt.push(3);
qt.push(4);
qt.push(5);
while (!qt.empty())
{
cout << qt.front() << " ";
qt.pop();
}
cout << endl;
}

3、queue的模拟实现
3.1、queue的结构一般的构建
一般方法的构建:
template<class T>
class queue {
private:
T* elements; // 存储元素的数组
int front; // 队列头部的索引
int rear; // 队列尾部的下一个位置索引
int capacity; // 队列的容量
};
3.2、queue的适配器模式构建
template<class T, class Container = list<T>>
class queue
{
private:
Container _con;
};
3.3、queue的主要接口函数
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_front();
}
T& back()
{
return _con.back();
}
const T& back() const
{
return _con.back();
}
T& front()
{
return _con.front();
}
const T& front() const
{
return _con.front();
}
size_t size() const
{
return _con.size();
}
bool empty() const
{
return _con.empty();
}
4、queue的模拟实现完整代码
4.1、一般方式
#include <iostream>
#include <stdexcept> // 用于抛出异常
template<class T>
class queue {
private:
T* elements; // 存储元素的数组
int front; // 队列头部的索引
int rear; // 队列尾部的下一个位置索引
int capacity; // 队列的容量
public:
// 构造函数
queue(int c) {
capacity = c;
elements = new T[capacity];
front = 0;
rear = 0;
}
// 析构函数
~queue() {
delete[] elements;
}
// 检查队列是否为空
bool isEmpty() const {
return front == rear;
}
// 检查队列是否已满
bool isFull() const {
return (rear + 1) % capacity == front;
}
// 入队操作
void enqueue(const T& value) {
if (isFull()) {
throw std::out_of_range("Queue is full");
}
elements[rear] = value;
rear = (rear + 1) % capacity;
}
// 出队操作
void dequeue() {
if (isEmpty()) {
throw std::out_of_range("Queue is empty");
}
front = (front + 1) % capacity;
}
// 访问队首元素
T& frontElement() {
if (isEmpty()) {
throw std::out_of_range("Queue is empty");
}
return elements[front];
}
// 获取队列大小
int size() const {
return (rear - front + capacity) % capacity;
}
};
// 使用示例
int main()
{
queue<int> q(5); // 创建一个容量为5的int类型队列
q.enqueue(1);
q.enqueue(2);
q.enqueue(3);
std::cout << "Front element: " << q.frontElement() << std::endl;
q.dequeue();
std::cout << "New front element: " << q.frontElement() << std::endl;
std::cout << "Queue size: " << q.size() << std::endl;
return 0;
}
4.2、泛型模式
namespace bit
{
template<class T, class Container = list<T>>
class queue
{
public:
void push(const T& x)
{
_con.push_back(x);
}
void pop()
{
_con.pop_front();
}
T& back()
{
return _con.back();
}
const T& back() const
{
return _con.back();
}
T& front()
{
return _con.front();
}
const T& front() const
{
return _con.front();
}
size_t size() const
{
return _con.size();
}
bool empty() const
{
return _con.empty();
}
private:
Container _con;
};
}
5、queue巩固练习题
5.1、最小栈
最小栈:在常数级时间内检索最小元素的栈
思路:
两个栈,一个存放原始数据,一个存放当前最小值(不断更新栈顶元素min)
class MinStack
{
public:
MinStack()
{}
//两个情况进值:
//1.最开始空栈
//2.更新栈顶min小值
void push(int val)
{
_st.push(val);
if (_minst.empty() || val <= _minst.top())
{
_minst.push(val);
}
}
void pop()
{
if (_minst.top() == _st.top())
{
_minst.pop();
}
_st.pop();
}
int top()
{
return _st.top();
}
int getMin()
{
return _minst.top();
}
stack<int> _st;
stack<int> _minst;
};
int main()
{
MinStack st;
st.push(2);
st.push(1);
st.push(3);
st.push(4);
st.push(0);
st.pop();
cout << st.top() << endl;
cout << st.getMin() << endl;
return 0;
}

5.2、栈的匹配(栈的压入和弹出序列)
满足栈的压入与出栈序列合理。
意思就是出栈序列,可满足栈的入栈序列,即”先进后出“。
思路:
1.先把入栈序列入栈
2.栈顶元素和出栈序列是否匹配
a、如果匹配就持续出数据,直到栈为空为止
b、如果不匹配,继续入栈
3.结束标志:a、入栈序列走完了 b、栈走完了,也不匹配,不合法的序列
class Solution
{
public:
bool IsPopOrder(vector<int>& pushV, vector<int>& popV)
{
int pushi = 0, popi = 0;
stack<int> st;
while (pushi < pushV.size())
{
st.push(pushV[pushi++]);
while (!st.empty() && st.top() == popV[popi])
{
++popi;
st.pop();
}
}
return st.empty();
}
};
int main()
{
Solution sol;
vector<int> pushV = { 1, 2, 3, 4, 5 };
//vector<int> popV = { 5, 4, 3, 2, 1 };
vector<int> popV = { 4, 5, 3, 2, 1 };
//vector<int> popV = { 4, 3, 5, 1, 2 };
// 检查出栈序列是否是可能的
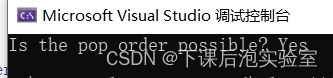
bool isPossiblePopOrder = sol.IsPopOrder(pushV, popV);
// 打印结果
cout << "Is the pop order possible? " << (isPossiblePopOrder ? "Yes" : "No") << endl;
return 0;
}
5.3、逆波兰表达式求值 (后缀表达式)
操作数在操作符之后的表达式,比如:abcd-*+ — 遇见运算符就开始计算
思路:
利用栈,栈处理操作数和运算符的顺序关系优先级,遇到操作数就入栈,遇到操作数就出栈操作数,运算结果继续入栈,再继续下一个操作数。
class Solution
{
public:
int evalRPN(vector<string>& tokens)
{
stack<int> st;
//写法2:set
set<string> s = { "+","-","*","/" };
for (auto& str : tokens)
{
//1.操作数入栈,遇到运算符运算
//写法1:穷举
//if (str == "+" || "-" == str || "*" == str || "/" == str)
//写法2:set -- 容器,搜索树
if(s.find(str) != s.end())
{
//是操作符,根据栈的性质
//先取的是右操作数,再是左操作数
int right = st.top();
st.pop();
int left = st.top();
st.pop();
//运算后的结果入栈
switch (str[0])//str[0] --- char整型与case参数匹配
{
case '+':
st.push(left + right);//操作数顺序还原
break;
case '-':
st.push(left - right);
break;
case '*':
st.push(left * right);
break;
case '/':
st.push(left / right);
break;
}
}
else
{
st.push(stoi(str));
}
}
return st.top();
}
};
int main()
{
Solution sol;
// 逆波兰表示法的表达式
vector<string> tokens = { "2", "1", "+", "3", "*" };
// 计算表达式的值
int result = sol.evalRPN(tokens);
// 打印结果
cout << "The result of the expression is: " << result << endl;
return 0;
}

5.4、两个栈实现队列
实现用两个栈模拟实现队列的”先进先出“。
思路:
利用两个栈相互倒,从而满足队列的性质
即:一个push栈进数据,push栈倒数据到一个pop栈,让pop栈出数据。
class MyQueue {
public:
MyQueue()
{}
void push(int x)
{
_pushst.push(x);
}
int pop()
{
int retpop = peek();
_popst.pop();
return retpop;
}
int peek()
{
if (_popst.empty())
{
//倒数据
while (!_pushst.empty())
{
_popst.push(_pushst.top());
_pushst.pop();
}
}
return _popst.top();
}
bool empty()
{
return _pushst.empty() && _popst.empty();
}
private:
stack<int> _pushst;
stack<int> _popst;
};
int main()
{
MyQueue qt;
qt.push(1);
qt.push(2);
qt.push(3);
qt.push(4);
qt.push(5);
while (!qt.empty())
{
printf("%d ", qt.peek());
qt.pop();
}
return 0;
}