数学杂谈之四：学习数学的方法

数学杂谈之一：数学的形态 https://blog.csdn.net/cnds123/article/details/137437208

数学杂谈之二：数学中的概念和理解 https://blog.csdn.net/cnds123/article/details/137500537

数学杂谈之三：数学思想方法 https://blog.csdn.net/cnds123/article/details/137559940

学习数学的方法和前文提到的数学方法不完全是一个意思。

“数学方法”指的是数学这门学科本身探索真理、发现规律和解决问题时所遵循和运用的一般方法，是数学发展和研究本身所依赖的科学方法论，体现了数学的本质特点。

“学习数学的方法”通常指的是人们获取和掌握数学知识的方式方法，着眼于个人如何高效获取数学知识，着重服务于教与学。包括如下方面：

概念理解和知识构建的途径

解题技巧和策略

利用教学资源、工具等辅助手段

培养数学思维习惯

个人学习计划和时间管理

等

“数学方法”和“学习数学的方法”两者虽有区别（关注焦点、应用范围、层次和阶段、目的性和实际应用等方面不同），但也存在内在联系（在目标、知识与技能、思维方式等方面存在内在联系），它们相辅相成，共同推动学生对数学素养的提高。

关于学习数学的方法，学习数学是一个多样化且个性化的过程，它依赖于个人的学习习惯、兴趣和能力。通用建议如下：

理解基础概念： 确保对基础概念的理解清晰，因为后续学习都基于这些概念。

练习和实践： 数学需要不断的练习和实践。解决问题、做练习题和参加数学竞赛都是提高数学能力的有效方法。

多角度学习： 如果一个方法无法理解，尝试从不同的角度或资源去学习。有时候换个解释方式就能让难题迎刃而解。

建立联系： 将数学与实际生活联系起来，这样可以增加学习的兴趣和动力。例如，观察数学在科学、工程和日常生活中的应用。

寻求帮助： 不要害羞于向老师、同学或在线资源求助。有时候别人的解释和指导能够加速你的理解和学习进程。

持之以恒： 数学需要持之以恒的学习，不能一蹴而就。每天保持一定的学习时间，持续积累知识和技能。

学好数学需要持之以恒地练习和理解数学概念、公式、定理、法则。

通过做大量的练习题来熟练运用各种公式、定理和法则，加深对其理解。整理和总结重要的概念、公式、定理和法则之间的关系，将不同的概念、公式、定理和法则进行联系，建立起它们之间的逻辑关系，有助于记忆和理解。

在数学学习过程中，强调结构化思维是非常重要的。这是因为数学是一门高度结构化的学科，它建立在一系列概念、原则和规则的基础上。结构化思维帮助学生理解和应用数学的核心概念、关系和方法，从而提高他们的数学思维能力。

任何事物都是结构化的。这是因为在自然界和人类社会中，事物都是由各种组成部分、要素或阶段组成的，这些组成部分之间存在着一定的联系和关系。这种内在的联系和关系构成了事物的结构。例如房屋，房屋的基本结构通常包括地基、地板、墙体、屋顶、门窗等组成部分。这些部分相互关联，构成了房屋的整体结构。

表述1：结构化思维是一种思考和解决问题的方式，它将复杂的问题或想法按照一定的逻辑关系和层次结构有序地组织起来。具有以下几个主要特点：

分解与层次化：将大的问题或概念分解成小的、可管理的部分，并按照一定的层次关系组织起来。

逻辑关联：通过因果关系、前后关系等逻辑关联，将各个部分联系起来，形成一个有机的整体。

可视化：常常采用树状结构图、思维导图等形式将思维过程可视化，有助于直观地把握全貌和细节。

表述2：还有人认为，结构化思维可以理解为一种将复杂问题拆解为简单问题并按照逻辑性和优先级为这些问题构建框架的思考方式。这种思考方式有助于我们更好地理解问题，找到解决问题的方法。

两种表述方式实际上是相辅相成的， 不存在实质性差异，只是侧重点和表达方式有所不同，都反映了结构化思维的本质:将混乱的整体有序地分解为部分，按照内在逻辑将部分重新组织，从而使复杂问题变得可管理。这种思维模式有助于我们更好地理解和解决复杂的问题。

结构化思维有利于提高思考的效率和质量，是处理复杂信息和解决复杂问题的有效方式，能够帮助我们更好地组织和理解复杂的信息。在数学领域，结构化思维非常重要，因为它能够帮助我们更好地理解数学概念、解决数学问题。

结构化思维在数学中具有重要意义。数学中所涵盖的知识点都不是孤立的，而是相互联系的。数学本身就是一门研究抽象结构的学科，其核心是探索各种数学对象之间的关系和规律。结构化思维有助于理解和把握数学对象的内在逻辑，发现不同对象之间的联系，从而推导出一般化的理论和公式。

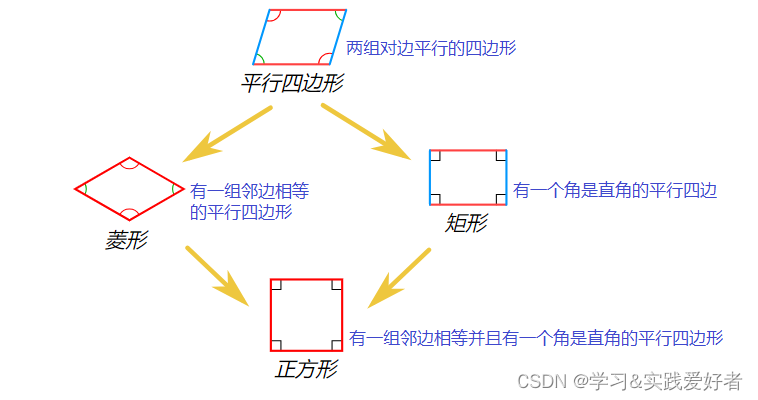
让数学知识结构化，更在于形成结构化思维。重视数学知识的方法建构、思想渗透等。“概念的抽象和下定义”一般流程是：观察分析典型案例和具体案例的共同表面特征，提炼和概括对象的本质特征、概念内涵和元素等。也就是说“下定义”表示几何对象，考虑了几何对象的分类，注意文字语言、符号语言、图形语言这三种语言转换。

由四个直线段围成的封闭平面图形称为一般四边形。如果对角线完全位于四边形内，则它是凸的，否则是凹的。下面是凸的四边形

附录

从数数开始的数学学习指南https://zhuanlan.zhihu.com/p/678367275

上最强学习方法——费曼学习法https://zhuanlan.zhihu.com/p/152547764

小平邦彦的数学学习方式https://www.zhihu.com/question/622134563/answer/3299706903

为什么突然感觉数学学习依靠积累而非智商?https://www.zhihu.com/question/630707081/answer/3368852361

学数学的真正意义https://www.zhihu.com/question/67237271