文章目录
- 前言
- 深度是个啥,高度又是啥
- Leetcode 104.二叉树的最大深度
- 题目讲解
- Leetcode 111.二叉树的最小深度
- 题目讲解
- Leetcode 222.完全二叉树的节点个数(优先掌握递归
- 题目讲解
- 总结
前言
今天将主要围绕 深度和高度 来展开
复习一下递归三部曲
- 确定递归函数的参数和返回值
- 确定终止条件
- 确定单层递归的逻辑
深度是个啥,高度又是啥
深度: 从根节点 到 最远叶子节点的距离 一般采用前序遍历

这三叉树的最大深度 为 3
高度 : 从最远叶子节点 到 根节点的距离 一般采用后续遍历
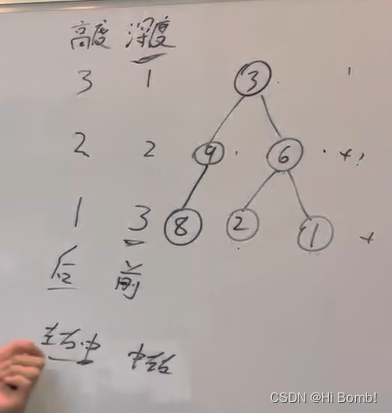
因为根节点的高度 就是 这颗二叉树的最大深度 今天的题都是用后续遍历做的
Leetcode 104.二叉树的最大深度
题目讲解
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int maxDepth(TreeNode root) {
// 按照高度即深度的思路 因为 深度 是按照后序算法来做的
if( root ==null)
{
return 0;
}
int leftHeight = maxDepth( root.left);
int rightHeight = maxDepth(root.right);
int Height = Math.max( leftHeight,rightHeight) +1;
return Height;
}
}
Leetcode 111.二叉树的最小深度
题目讲解
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int minDepth(TreeNode root) {
if( root == null)
{
return 0;
}
int leftHeight = minDepth(root.left);
int rightHeight = minDepth(root.right);
if( root.left!=null && root.right==null)
{
return leftHeight+1;
}
if( root.right!= null && root.left==null)
{
return rightHeight+1;
}
return Math.min( rightHeight,leftHeight)+1;
}
}
Leetcode 222.完全二叉树的节点个数(优先掌握递归
题目讲解
/**
* Definition for a binary tree node.
* public class TreeNode {
* int val;
* TreeNode left;
* TreeNode right;
* TreeNode() {}
* TreeNode(int val) { this.val = val; }
* TreeNode(int val, TreeNode left, TreeNode right) {
* this.val = val;
* this.left = left;
* this.right = right;
* }
* }
*/
class Solution {
public int countNodes(TreeNode root) {
//
if( root ==null)
return 0;
TreeNode left = root.left;
TreeNode right = root.right;
int leftdepth =0;
int rightdepth=0;
while( left!= null)
{
left= left.left;
leftdepth++;
}
while( right!=null)
{
right=right.right;
rightdepth++;
}
if( rightdepth== leftdepth)
{
return (2<<leftdepth)-1;
}
return countNodes(root.left)+countNodes(root.right)+1;
}
}
总结
无论是求二叉树的最大深度还是最小深度 我都采用了后续遍历的方式
左右 中 +1到父节点 加1再到根节点
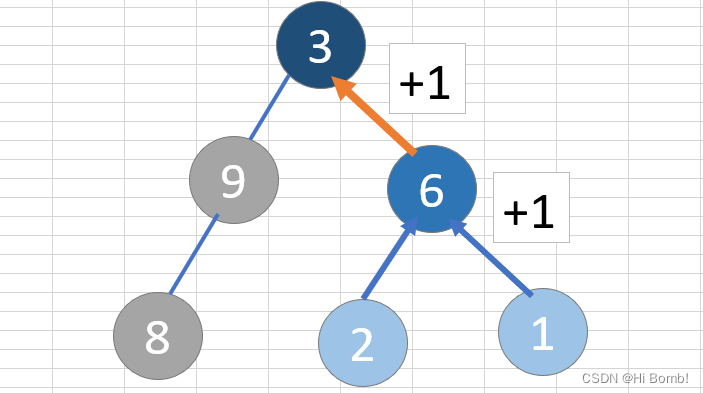
虽然不喜欢糊弄事 不过接下来还要配环境就到这吧