贪心算法一般分为如下四步:
- 将问题分解为若干个子问题
- 找出适合的贪心策略
- 求解每一个子问题的最优解
- 将局部最优解堆叠成全局最优解
做题的时候,只要想清楚 局部最优 是什么,如果推导出全局最优,其实就够了。
假设你是一位很棒的家长,想要给你的孩子们一些小饼干。但是,每个孩子最多只能给一块饼干。
对每个孩子 i,都有一个胃口值 g[i],这是能让孩子们满足胃口的饼干的最小尺寸;并且每块饼干 j,都有一个尺寸 s[j] 。如果 s[j] >= g[i],我们可以将这个饼干 j 分配给孩子 i ,这个孩子会得到满足。你的目标是尽可能满足越多数量的孩子,并输出这个最大数值。
455. 分发饼干
示例 1:
输入: g = [1,2,3], s = [1,1] 输出: 1 解释: 你有三个孩子和两块小饼干,3个孩子的胃口值分别是:1,2,3。 虽然你有两块小饼干,由于他们的尺寸都是1,你只能让胃口值是1的孩子满足。 所以你应该输出1。
思路:这里的局部最优就是大饼干喂给胃口大的,充分利用饼干尺寸喂饱一个,全局最优就是喂饱尽可能多的小孩。
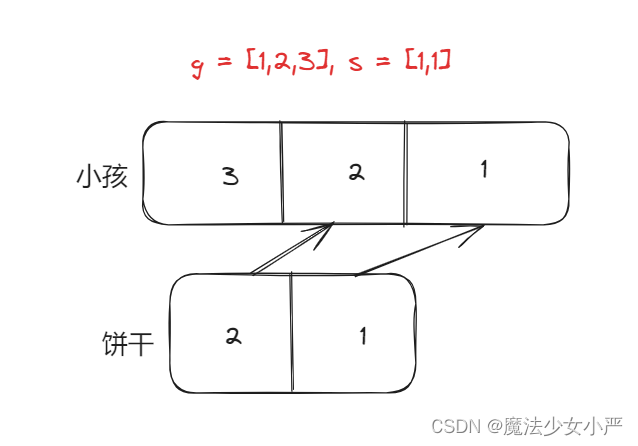
这里先遍历小孩,找到当前最大尺寸饼干能满足的小孩
class Solution {
public int findContentChildren(int[] g, int[] s) {
//将饼干和胃口排序
Arrays.sort(g);
Arrays.sort(s);
int total_child=0;
int start=s.length-1;//start指向当前最大的饼干
//g是小孩,s是饼干
//遍历小孩,先满足最大胃口的小孩
for(int i=g.length-1;i>=0;i--){
if(start>=0&&s[start]>=g[i]){
start--;
total_child++;
}
}
return total_child;
}
}也可以让小饼干满足小胃口的孩子.
这里先遍历饼干,找到满足当前最小胃口的饼干
class Solution {
public int findContentChildren(int[] g, int[] s) {
//将饼干和胃口排序
Arrays.sort(g);
Arrays.sort(s);
int total_child=0;
int start=0;//start指向当前小的胃口
//g是小孩,s是饼干
//遍历饼干
for(int i=0;i<s.length;i++){
if(start<g.length&&g[start]<=s[i]){
start++;
total_child++;
}
}
return total_child;
}
}376. 摆动序列
如果连续数字之间的差严格地在正数和负数之间交替,则数字序列称为 摆动序列 。第一个差(如果存在的话)可能是正数或负数。仅有一个元素或者含两个不等元素的序列也视作摆动序列。
-
例如,
[1, 7, 4, 9, 2, 5]是一个 摆动序列 ,因为差值(6, -3, 5, -7, 3)是正负交替出现的。 - 相反,
[1, 4, 7, 2, 5]和[1, 7, 4, 5, 5]不是摆动序列,第一个序列是因为它的前两个差值都是正数,第二个序列是因为它的最后一个差值为零。
子序列 可以通过从原始序列中删除一些(也可以不删除)元素来获得,剩下的元素保持其原始顺序。
给你一个整数数组 nums ,返回 nums 中作为 摆动序列 的 最长子序列的长度 。
示例 1:
输入:nums = [1,7,4,9,2,5] 输出:6 解释:整个序列均为摆动序列,各元素之间的差值为 (6, -3, 5, -7, 3)
思路:删除单调坡度上的结点(不包括单调坡度两端的节点)
实际操作上,其实连删除的操作都不用做,因为题目要求的是最长摆动子序列的长度,所以只需要统计数组的峰值数量就可以了(相当于是删除单一坡度上的节点,然后统计长度)
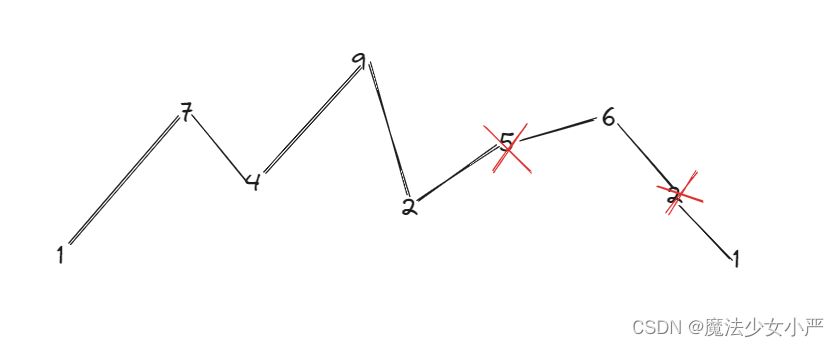
在计算是否有峰值的时候,遍历的下标 i ,计算 prediff(nums[i] - nums[i-1]) 和 curdiff(nums[i+1] - nums[i]),如果prediff < 0 && curdiff > 0 或者 prediff > 0 && curdiff < 0 此时就有波动就需要统计。
但本题要考虑三种情况:
- 情况一:上下坡中有平坡
- 情况二:数组首尾两端
- 情况三:单调坡中有平坡
1.情况一:上下坡中有平坡
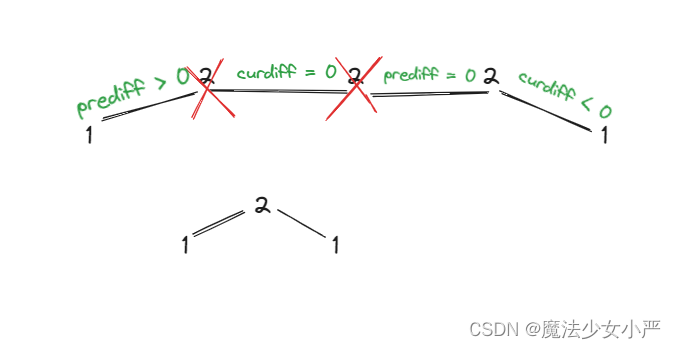
当 i 指向第一个 2 的时候,prediff > 0 && curdiff = 0 ,当 i 指向最后一个 2 的时候 prediff = 0 && curdiff < 0。
删左面三个 2 的规则,那么 当 prediff = 0 && curdiff < 0 也要记录一个峰值,因为他是把之前相同的元素都删掉留下的峰值。
所以我们记录峰值的条件应该是: (preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0),为什么这里允许 prediff == 0 ,就是为了 上面我说的这种情况。
2.情况二:数组首尾两端
如果只有两个元素,这里我们可以写死,只有两个元素且元素不同,那么结果为 2。
不写死的话,如何和我们的判断规则结合在一起呢?
那么为了规则统一,针对序列[1,2,1],可以假设为[1,1,2,1],这样它就有坡度了即 preDiff = 0
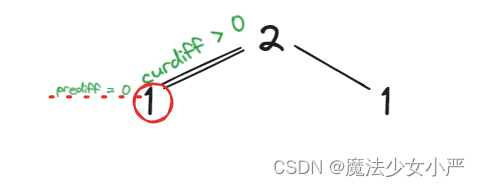
result 初始为 1(默认最右面有一个峰值)
3.情况三:单调坡中有平坡
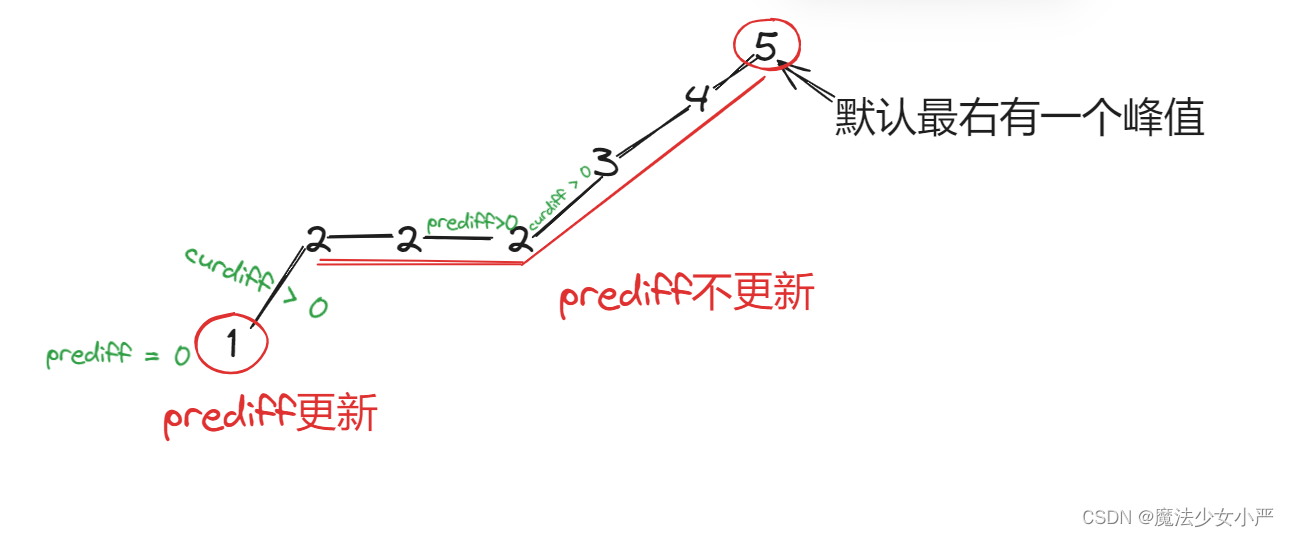
(preDiff <= 0 && curDiff > 0) || (preDiff >= 0 && curDiff < 0)会导致我们在单调坡中有平坡的情况发生误判,如图中的2

改进:我们只需要在 这个坡度 摆动变化的时候,更新 prediff 就行,这样 prediff 在 单调区间有平坡的时候 就不会发生变化
class Solution {
public int wiggleMaxLength(int[] nums) {
//仅有一个元素也视作摆动序列
if(nums.length<=1) return nums.length;
int preDiff=0;//与前差值(默认第一个数的前面的坡度为0)
int curDiff=0;//与后差值
int result=1;//记录峰值,默认最右端的数是摆动序列的一员
//i<nums.length-1,默认最后一个数为峰值,所有遍历到倒数第二个数
for(int i=0;i<nums.length-1;i++){
curDiff=nums[i+1]-nums[i];
if(preDiff>=0&&curDiff<0||preDiff<=0&&curDiff>0){
result++;
preDiff=curDiff;//只有摆动变化才更新prediff;
}
}
return result;
}
}53. 最大子数组和
给你一个整数数组 nums ,请你找出一个具有最大和的连续子数组(子数组最少包含一个元素),返回其最大和。
子数组
是数组中的一个连续部分。
示例 1:
输入:nums = [-2,1,-3,4,-1,2,1,-5,4] 输出:6 解释:连续子数组 [4,-1,2,1] 的和最大,为 6
方法1:
暴力解法:
第一层 for 就是设置起始位置,第二层 for 循环遍历数组寻找最大值
方法2:
贪心:
局部最优:当前“连续和”为负数的时候立刻放弃,从下一个元素重新计算“连续和”,因为负数加上下一个元素 “连续和”只会越来越小。
全局最优:选取最大“连续和”

class Solution {
public int maxSubArray(int[] nums) {
int sum = Integer.MIN_VALUE;
int count=0;
for(int i=0;i<nums.length;i++){
count+=nums[i];
if(count>sum){//取区间的累计最大值,因为连续子区间的和可能小于0;
sum=count;
}
if(count<=0) count=0;//加上负数一定会拉低连续子数组的和,重置子序列位置
}
return sum;
}
}79. 填充
时间限制:1.000S 空间限制:256MB
题目描述
有一个长度为 n 的 01 串,其中有一些位置标记为 ?,这些位置上可以任意填充 0 或者 1,请问如何填充这些位置使得这个 01 串中出现互不重叠的 00 和 11 子串最多,输出子串个数。
输入描述
输入一行包含一个字符串。
输出描述
输出一行包含一个整数表示答案。
输入示例
1110?0输出示例
2提示信息
如果在问号处填 0 ,则最多出现一个 00 和一个 11:111000。
对于所有评测用例,1 ≤ n ≤ 1000000。
思路:很多人把这题想复杂了,你根本不需要考虑?是0还是1,无所谓,我们把x?,?x,xx,??(x代表1或者0)都当作子串了,如果遇见子串,走两步,i=i+2,如果不是子串,走一步,让下一个数去匹配
代码参考:
import java.util.*;
public class Main {
public static void main(String args[]) {
Scanner scanner=new Scanner(System.in);
String s=scanner.next();
int count=0;
for(int i=0;i<s.length()-1;){
if(s.charAt(i)==s.charAt(i+1)||s.charAt(i+1)=='?'||s.charAt(i)=='?'){
count++;i=i+2;
}else{i++;}
}
System.out.println(count);
}
}