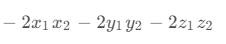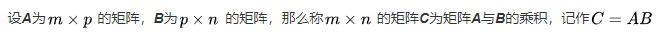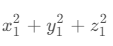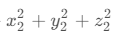文章目录
- 一、计算两组点之间的欧式距离
- 二、举例
- 三、中间结果输出
一、计算两组点之间的欧式距离
def square_distance(src, dst):
"""
Calculate Euclid distance between each two points.
src^T * dst = xn * xm + yn * ym + zn * zm;
sum(src^2, dim=-1) = xn*xn + yn*yn + zn*zn;
sum(dst^2, dim=-1) = xm*xm + ym*ym + zm*zm;
dist = (xn - xm)^2 + (yn - ym)^2 + (zn - zm)^2
= sum(src**2,dim=-1)+sum(dst**2,dim=-1)-2*src^T*dst
Input:
src: source points, [B, N, C]
dst: target points, [B, M, C]
Output:
dist: per-point square distance, [B, N, M]
"""
B, N, _ = src.shape
_, M, _ = dst.shape
dist = -2 * torch.matmul(src, dst.permute(0, 2, 1))
dist += torch.sum(src ** 2, -1).view(B, N, 1)
dist += torch.sum(dst ** 2, -1).view(B, 1, M)
return dist
🍉解释:
B, N, _ = src.shape:获取输入源点和目标点的形状信息,其中 B 表示批量大小,N 表示源点的数量
_, M, _ = dst.shape:M 表示目标点的数量,C 表示每个点的维度
dist = -2 * torch.matmul(src, dst.permute(0, 2, 1)):这一步计算了两组点之间的叉乘积
dst.permute(0, 2, 1):将目标点张量 dst 的第二维和第三维进行交换,以便进行点积
同理,src为N x C,dst为M x C,需要将M x C转置成C x M才可以进行点积(N x C)·(C x M)torch.matmul:计算源点和目标点之间的点积,结果 dist 是一个形状为 [B, N, M] 的张量,表示每对源点和目标点之间的点积
dist += torch.sum(src ** 2, -1).view(B, N, 1):计算了源点和目标点的平方和,并将其广播到与 dist 相同的形状
torch.sum(src ** 2, -1):计算张量 src 中每个点的平方和,src ^2 将 src 中的每个元素都平方,然后 torch.sum 函数对最后一个维度(即 -1 所代表的维度)进行求和,最后一个维度被求和消除。- 假设 src 张量的形状是 [B, N, D],其中 B 表示批量大小,N 表示点的数量,D 表示每个点的维度。那么 torch.sum(src ** 2, -1) 的结果形状将是 [B, N],其中每个元素表示了原张量中相应位置点的平方和
view(B, N, 1):对张量调整到[B, N, 1],以便与后续的计算相兼容
dist += torch.sum(dst ** 2, -1).view(B, 1, M):将这些平方和加到 dist 上,以完成欧氏距离的计算
dist:张量,函数返回每对源点和目标点之间的欧氏距离的平方,形状为 [B, N, M]
计算欧式距离的平方等价于下方等式
(
x
1
−
x
2
)
2
+
(
y
1
−
y
2
)
2
+
(
z
1
−
z
2
)
2
(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}+(z_{1}-z_{2})^{2}
(x1−x2)2+(y1−y2)2+(z1−z2)2=
x
1
2
+
y
1
2
+
z
1
2
+
x
2
2
+
y
2
2
+
z
2
2
−
2
x
1
x
2
−
2
y
1
y
2
−
2
z
1
z
2
x_{1}^{2}+y_{1}^{2}+z_{1}^{2}+x_{2}^{2}+y_{2}^{2}+z_{2}^{2}-2x_{1}x_{2}-2y_{1}y_{2}-2z_{1}z_{2}
x12+y12+z12+x22+y22+z22−2x1x2−2y1y2−2z1z2
二、举例
假设有两组点,分别是 src 和 dst:
import torch
def square_distance(src, dst):
B, N, _ = src.shape
_, M, _ = dst.shape
dist = -2 * torch.matmul(src, dst.permute(0, 2, 1))
dist += torch.sum(src ** 2, -1).view(B, N, 1)
dist += torch.sum(dst ** 2, -1).view(B, 1, M)
return dist
# 定义源点和目标点
src = torch.tensor([[[1, 2, 3], [4, 5, 6]]]) # shape: [1, 2, 3]
dst = torch.tensor([[[7, 8, 9], [10, 11, 12], [13, 14, 15]]]) # shape: [1, 3, 3]
dist = square_distance(src, dst)
print(dist)
结果

例如
(
7
−
1
)
2
+
(
8
−
2
)
2
+
(
9
−
3
)
2
=
108
(7-1)^{2}+(8-2)^{2}+(9-3)^{2}=108
(7−1)2+(8−2)2+(9−3)2=108
三、中间结果输出
- 对于
dist = -2 * torch.matmul(src, dst.permute(0, 2, 1))
对于torch.sum(src ** 2, -1)

tensor([[14, 77]]):这是一个形状为 (1, 2) 的张量,表示一个批次中有两个源点,每个源点有两个坐标分量。具体地,它包含了以下信息:第一个源点的坐标是 (14, 77)。- 对于torch.sum(src ** 2, -1).view(B, N, 1)

tensor([[[14], [77]]]):这是一个形状为 (1, 2, 1) 的张量,表示一个批次中有两个目标点,每个目标点有一个坐标分量。具体地,它包含了以下信息:
第一个目标点的坐标是 (14)
第二个目标点的坐标是 (77)- 对于
dist += torch.sum(src ** 2, -1).view(B, N, 1)
- 对于
torch.sum(dst ** 2, -1)
- 对于
torch.sum(src ** 2, -1).view(B, N, 1)
- 对于
dist += torch.sum(src ** 2, -1).view(B, N, 1)