吴恩达机器学习：均值聚类法（K-means Clustering）

news2024/11/25 18:27:37

在本练习中，您将实现K-means算法并将其用于图像压缩。

  • 您将从一个样本数据集开始，该数据集将帮助您直观地了解K-means算法的工作原理。
  • 之后，您将使用K-means算法进行图像压缩，将图像中出现的颜色数量减少到该图像中最常见的颜色。

文章目录

  • 1-实现K-means
    • 1.2计算质心意味着
  • 2-样本数据集上的K-means
  • 3-随机初始化
  • 4-使用K-means进行图像压缩
    • 4.1数据集加载图像
    • 4.2图像像素上的K-Means
    • 4.3压缩图像

import numpy as np
import matplotlib.pyplot as plt
from utils import *

%matplotlib inline

1-实现K-means

K-means算法是一种自动将相似数据点聚类在一起的方法。

  • 具体来说，你会得到一套训练{𝑥1,……,𝑥(𝑚)}，并且您希望将数据分组为几个有凝聚力的“集群”。
  • K-means是一个迭代过程
    • 首先猜测初始质心，然后
    • 通过优化此猜测
      • 反复将示例指定给它们最近的质心
      • 根据指定重新计算质心。
        在伪码中，K-means算法如下：
# Initialize centroids
# K is the number of clusters
#初始化质心
#K是簇的数量
centroids = kMeans_init_centroids(X, K)

for iter in range(iterations):
    # Cluster assignment step: 
    # Assign each data point to the closest centroid. 
    # idx[i] corresponds to the index of the centroid 
    # assigned to example i
    #群集分配步骤：
	#将每个数据点指定给最近的质心。
	#idx[i]对应于质心的索引
	#分配给示例i
    idx = find_closest_centroids(X, centroids)

    # Move centroid step: 
    # Compute means based on centroid assignments
    #移动质心步长：
	#基于质心分配计算均值
    centroids = compute_means(X, idx, K)
  • 算法的内部循环重复执行两个步骤：
    • （i） 分配每个训练示例𝑥(𝑖) 以及
    • （ii）使用分配给每个质心的点重新计算每个质心的平均值。
  • 这个𝐾-均值算法将总是收敛到质心的某个最终均值集。
  • 然而，收敛解可能并不总是理想的，并且取决于质心的初始设置。
    • 因此，在实践中，K-means算法通常在不同的随机初始化下运行几次。
    • 从不同的随机初始化中在这些不同的解决方案之间进行选择的一种方法是选择具有最低成本函数值（失真）的解决方案。

在接下来的部分中，您将分别实现K-means算法的两个阶段。

  • 您将从完成find_closest_centroid开始，然后继续完成compute_centroids。

1.1寻找最接近的质心
在K-means算法的“聚类分配”阶段，该算法分配每个训练示例𝑥(𝑖)到其最近的质心，给定质心的当前位置。

练习1
您的任务是完成find_closest_centroids中的代码。

  • 此函数获取数据矩阵X和质心内所有质心的位置。
  • 它应该输出一个一维数组idx（与X具有相同数量的元素），该数组保存最近质心的索引（{1，…，𝐾}，𝐾是质心的总数）。
  • 具体来说，对于每个例子𝑥(𝑖) 我们设置
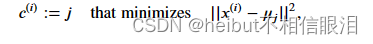
    在这里插入图片描述
  • 𝑐^(i)是最接近于其的质心的索引(对应于起始代码中的idx[i])，
  • 而u𝑗是𝑗的第一个质心的位置(值)。(存储在启动代码中的质心中)

如果你遇到了困难，你可以查看下面单元格后呈现的提示，以帮助你实现。
正确答案👇

def find_closest_centroids(X, centroids):

    # Set K
    K = centroids.shape[0]

    # You need to return the following variables correctly
    idx = np.zeros(X.shape[0], dtype=int)

    ### START CODE HERE ###
    for i in range(X.shape[0]):
        # Array to hold distance between X[i] and each centroids[j]
        distance = [] 
        for j in range(centroids.shape[0]):
            norm_ij = np.linalg.norm(X[i]-centroids[j])
            distance.append(norm_ij)
        
        idx[i] = np.argmin(distance)
    ### END CODE HERE ###
    return idx

自己写的答案👇

# UNQ_C1
# GRADED FUNCTION: find_closest_centroids

def find_closest_centroids(X, centroids):
    """
    Computes the centroid memberships for every example
    
    Args:
        X (ndarray): (m, n) Input values      
        centroids (ndarray): k centroids
    
    Returns:
        idx (array_like): (m,) closest centroids
    
    """

    # Set K
    K = centroids.shape[0]

    # You need to return the following variables correctly
    idx = np.zeros(X.shape[0], dtype=int)

    m=X.shape[0]

    ### START CODE HERE ###
    for i in range(m):
        min = float('inf')
        for j in range(K):
            L=np.linalg.norm(X[i]-centroids[j])
            if L<min:
                min=L
                idx[i]=j

    ### END CODE HERE ###
    
    return idx

现在，让我们使用示例数据集检查您的实现

# Load an example dataset that we will be using
X = load_data()

下面的代码打印变量X中的前五个元素和变量的维度

print("First five elements of X are:\n", X[:5]) 
print('The shape of X is:', X.shape)

First five elements of X are:
 [[1.84207953 4.6075716 ]
 [5.65858312 4.79996405]
 [6.35257892 3.2908545 ]
 [2.90401653 4.61220411]
 [3.23197916 4.93989405]]
The shape of X is: (300, 2)

# Select an initial set of centroids (3 Centroids)
initial_centroids = np.array([[3,3], [6,2], [8,5]])

# Find closest centroids using initial_centroids
idx = find_closest_centroids(X, initial_centroids)

# Print closest centroids for the first three elements
print("First three elements in idx are:", idx[:3])

# UNIT TEST
from public_tests import *

find_closest_centroids_test(find_closest_centroids)


First three elements in idx are: [0 2 1]
All tests passed!

Expected Output:

First three elements in idx are [0 2 1]

1.2计算质心意味着

给定每个点到质心的分配，算法的第二阶段为每个质心重新计算分配给它的点的平均值。
练习2
请完成下面的compute_centroids，以重新计算每个质心的值

  • 具体来说，对于每个质心𝜇𝑘我们设置
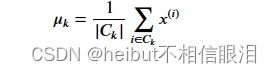
    在这里插入图片描述
    • 𝐶𝑘是分配给质心的一组示例𝑘
    • |𝐶𝑘|是集合中的示例数𝐶𝑘

具体来说，如果有两个例子𝑥3和𝑥5分配给质心𝑘=2，则应该更新𝜇2=1/2(𝑥3+𝑥5).
如果遇到问题，可以查看下面单元格后面的提示，以帮助您实现。

def compute_centroids(X, idx, K):
    """
    Returns the new centroids by computing the means of the 
    data points assigned to each centroid.
    
    Args:
        X (ndarray):   (m, n) Data points
        idx (ndarray): (m,) Array containing index of closest centroid for each 
                       example in X. Concretely, idx[i] contains the index of 
                       the centroid closest to example i
        K (int):       number of centroids
    
    Returns:
        centroids (ndarray): (K, n) New centroids computed
    """
    
    # Useful variables
    m, n = X.shape

    # You need to return the following variables correctly
    centroids = np.zeros((K, n))

    ### START CODE HERE ###
    for k in range(K):   
        points = X[idx == k]
        # Your code here to get a list of all data points in X assigned to centroid k  
        centroids[k] = np.mean(points,axis=0)
        # Your code here to compute the mean of the points assigned
    ### END CODE HERE ## 

    return centroids

我写的且让chat修改过的👇
在这里插入图片描述

K = 3
centroids = compute_centroids(X, idx, K)

print("The centroids are:", centroids)

# UNIT TEST
compute_centroids_test(compute_centroids)


The centroids are: [[2.42830111 3.15792418]
 [5.81350331 2.63365645]
 [7.11938687 3.6166844 ]]
All tests passed!

Expected Output:

2.42830111 3.15792418

5.81350331 2.63365645

7.11938687 3.6166844

2-样本数据集上的K-means

在完成上面的两个函数（find_closest_centroids和compute_centroid）后，下一步是在玩具2D数据集上运行K-means算法，以帮助您了解K-means是如何工作的。

  • 我们鼓励您看看下面的函数（run_kMeans），了解它是如何工作的。
  • 请注意，该代码调用您在循环中实现的两个函数。

当您运行下面的代码时，它将生成一个可视化，在每次迭代中逐步了解算法的进度。
最后，您的图应该如图1所示。
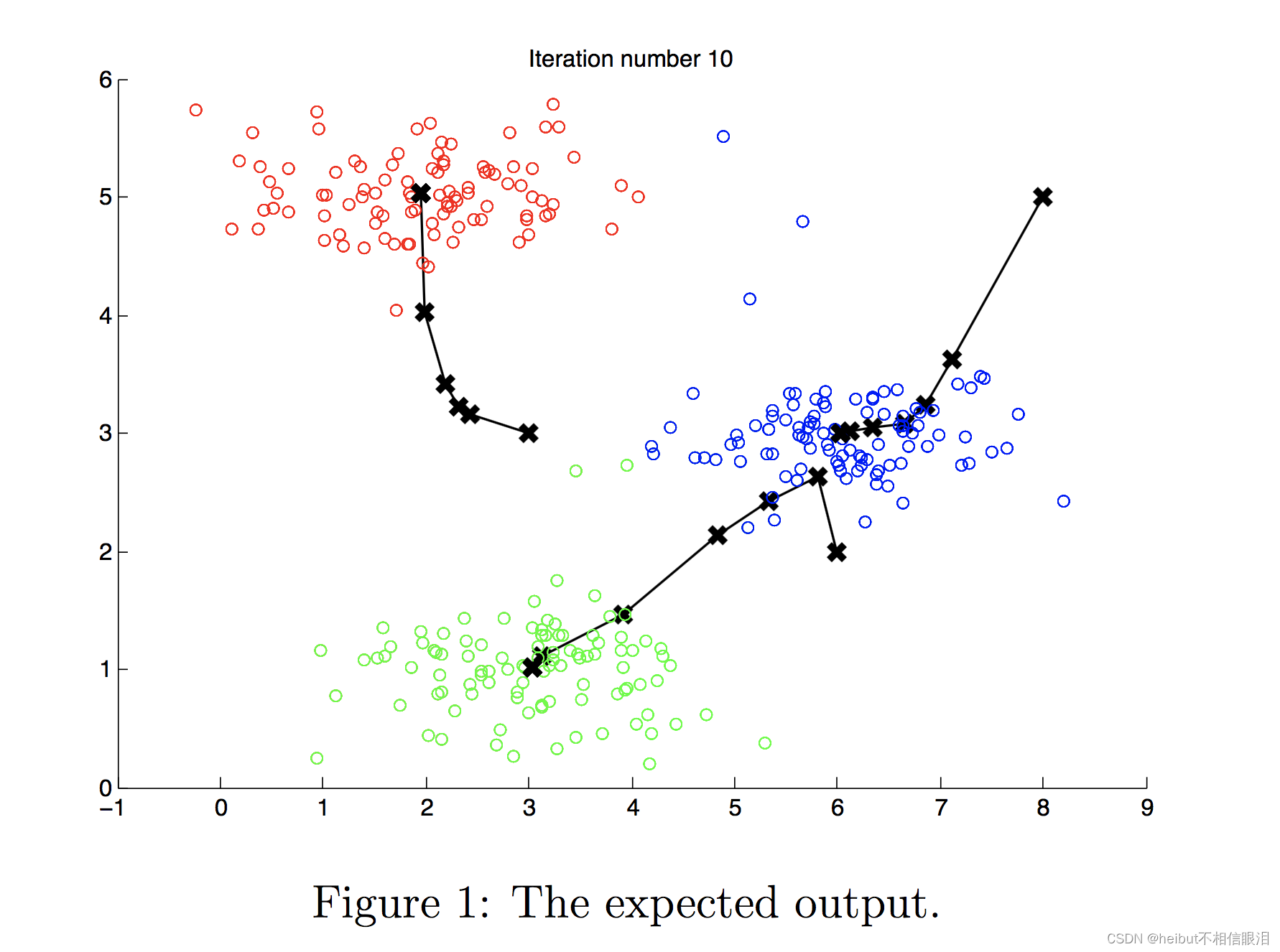
在这里插入图片描述
注意：您不需要为这个部分实现任何东西。只需运行下面提供的代码

# You do not need to implement anything for this part

def run_kMeans(X, initial_centroids, max_iters=10, plot_progress=False):
    """
    Runs the K-Means algorithm on data matrix X, where each row of X
    is a single example
    """
    """
	在数据矩阵X上运行K-Means算法，其中X的每一行
	只是一个例子
	"""
    # Initialize values
    m, n = X.shape
    K = initial_centroids.shape[0]
    centroids = initial_centroids
    previous_centroids = centroids    
    idx = np.zeros(m)
    
    # Run K-Means
    for i in range(max_iters):
        
        #Output progress
        print("K-Means iteration %d/%d" % (i, max_iters-1))
        
        # For each example in X, assign it to the closest centroid
        idx = find_closest_centroids(X, centroids)
        
        # Optionally plot progress
        if plot_progress:
            plot_progress_kMeans(X, centroids, previous_centroids, idx, K, i)
            previous_centroids = centroids
            
        # Given the memberships, compute new centroids
        centroids = compute_centroids(X, idx, K)
    plt.show() 
    return centroids, idx

# Load an example dataset
X = load_data()

# Set initial centroids
initial_centroids = np.array([[3,3],[6,2],[8,5]])
K = 3

# Number of iterations
max_iters = 10

centroids, idx = run_kMeans(X, initial_centroids, max_iters, plot_progress=True)

K-Means iteration 0/9
K-Means iteration 1/9
K-Means iteration 2/9
K-Means iteration 3/9
K-Means iteration 4/9
K-Means iteration 5/9
K-Means iteration 6/9
K-Means iteration 7/9
K-Means iteration 8/9
K-Means iteration 9/9

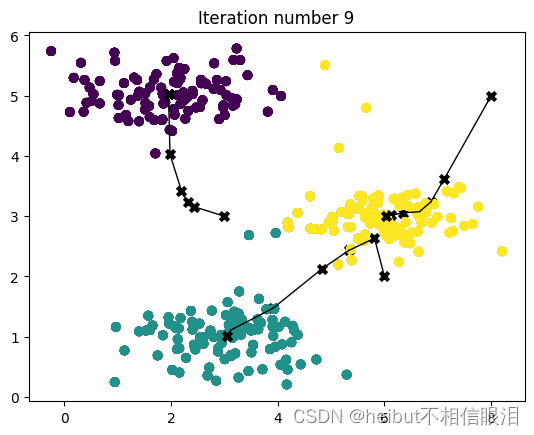
在这里插入图片描述

3-随机初始化

示例数据集的质心的初始分配经过设计，您将看到与图1中相同的图。在实践中，初始化质心的一个好策略是从训练集中随机选择示例。
在练习的这一部分中，您应该了解函数kMeans_int_centroids是如何实现的。

  • 代码首先随机打乱示例的索引（使用np.srandom.permutation()）。
  • 然后，它选择第一个𝐾 基于索引的随机排列的示例。
    • 这允许随机选择示例，而不存在两次选择同一示例的风险。

注意：对于练习的这一部分，您不需要进行任何实现。

# You do not need to modify this part

def kMeans_init_centroids(X, K):
    """
    This function initializes K centroids that are to be 
    used in K-Means on the dataset X
    
    Args:
        X (ndarray): Data points 
        K (int):     number of centroids/clusters
    
    Returns:
        centroids (ndarray): Initialized centroids
    """
    
    # Randomly reorder the indices of examples
    randidx = np.random.permutation(X.shape[0])
    
    # Take the first K examples as centroids
    centroids = X[randidx[:K]]
    
    return centroids

4-使用K-means进行图像压缩

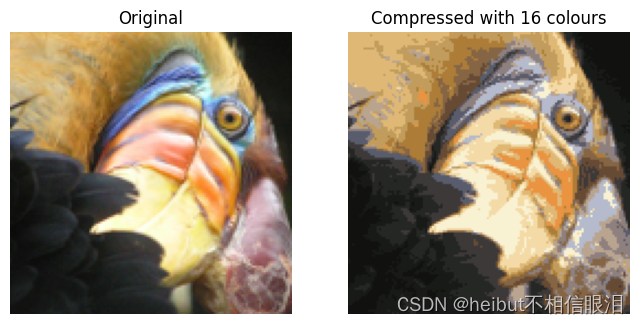
在本练习中，您将把K-means应用于图像压缩。

  • 在图像2的直接24位颜色表示中 ，每个像素表示为指定红色、绿色和蓝色强度值的三个8位无符号整数（范围从0到255）。这种编码通常被称为RGB编码。
  • 我们的图像包含数千种颜色，在这部分练习中，您将把颜色的数量减少到16种。
  • 通过进行这种缩小，可以以有效的方式表示（压缩）照片。
  • 具体来说，您只需要存储16种选定颜色的RGB值，对于图像中的每个像素，您现在只需要存储该位置的颜色索引（其中仅需要4位来表示16种可能性）。

在本部分中，您将使用K-means算法来选择将用于表示压缩图像的16种颜色。

  • 具体来说，您将把原始图像中的每个像素都作为一个数据示例，并使用K-means算法来找到在三维RGB空间中对像素进行最佳分组（聚类）的16种颜色。
  • 计算出图像上的簇质心后，将使用16种颜色替换原始图像中的像素。
    在这里插入图片描述
    2.本练习中使用的照片属于Frank Wouters，经其许可使用。

4.1数据集加载图像

首先，您将使用matplotlib读取原始图像，如下所示。

# Load an image of a bird
original_img = plt.imread('bird_small.png')

可视化图像
您可以使用下面的代码可视化刚刚加载的图像。

# Visualizing the image
plt.imshow(original_img)

在这里插入图片描述
检查变量的尺寸
和往常一样，您将打印出变量的形状，以便更熟悉数据。

print("Shape of original_img is:", original_img.shape)

Shape of original_img is: (128, 128, 3)

如您所见，这将创建一个三维矩阵original_img，其中

  • 前两个索引标识像素位置，第三个索引表示红色、绿色或蓝色。

例如，original_img[50，33，2]给出第50行和第33列像素的蓝色强度。
处理数据
要调用run_kMeans，首先需要将矩阵original_img转换为二维矩阵。

  • 下面的代码重塑矩阵original_img以创建𝑚*3. 像素颜色矩阵（其中𝑚=16384=128×128)
# Divide by 255 so that all values are in the range 0 - 1
original_img = original_img / 255

# Reshape the image into an m x 3 matrix where m = number of pixels
# (in this case m = 128 x 128 = 16384)
# Each row will contain the Red, Green and Blue pixel values
# This gives us our dataset matrix X_img that we will use K-Means on.
#将图像重塑为m x 3矩阵，其中m=像素数
#（在这种情况下，m=128 x 128=16384）
#每行将包含红色、绿色和蓝色像素值
#这给了我们数据集矩阵X_img，我们将对其使用K-Means。

X_img = np.reshape(original_img, (original_img.shape[0] * original_img.shape[1], 3))

举例说明上述代码的作用👇
在这里插入图片描述

4.2图像像素上的K-Means

现在，运行下面的单元格对预处理的图像运行K-Means。

# Run your K-Means algorithm on this data
# You should try different values of K and max_iters here
K = 16                       
max_iters = 10               

# Using the function you have implemented above. 
initial_centroids = kMeans_init_centroids(X_img, K) 

# Run K-Means - this takes a couple of minutes
centroids, idx = run_kMeans(X_img, initial_centroids, max_iters) 

K-Means iteration 0/9
K-Means iteration 1/9
K-Means iteration 2/9
K-Means iteration 3/9
K-Means iteration 4/9
K-Means iteration 5/9
K-Means iteration 6/9
K-Means iteration 7/9
K-Means iteration 8/9
K-Means iteration 9/9

print("Shape of idx:", idx.shape)
print("Closest centroid for the first five elements:", idx[:5])

4.3压缩图像

找到顶部后𝐾=16颜色来表示图像，现在可以使用find_closest_centroids函数将每个像素位置分配给其最近的质心。

  • 这允许您使用每个像素的质心指定来表示原始图像。
  • 请注意，您已经显著减少了描述图像所需的位数。
    • 原始图像需要128×128中的每一个24位 像素位置，导致总大小为128×128×24=393216 位。
    • 新的表示需要以16种颜色的字典形式的一些开销存储，每种颜色需要24位，但图像本身每个像素位置只需要4位。
    • 因此，最终使用的位数为16×24+128×128×4=65920 这对应于将原始图像压缩大约6倍。
# Represent image in terms of indices
X_recovered = centroids[idx, :] 

# Reshape recovered image into proper dimensions
X_recovered = np.reshape(X_recovered, original_img.shape)

idx是索引，centroids是值，X_recovered是每一个元素对应的值。

最后，您可以通过仅基于质心指定重建图像来查看压缩的效果。

  • 具体来说，您可以将每个像素位置替换为指定给它的质心的平均值。
  • 图3显示了我们获得的重建。即使生成的图像保留了原始图像的大部分特征，我们也会看到一些压缩伪影。
    在这里插入图片描述
# Display original image
fig, ax = plt.subplots(1,2, figsize=(8,8))
plt.axis('off')

ax[0].imshow(original_img*255)
ax[0].set_title('Original')
ax[0].set_axis_off()


# Display compressed image
ax[1].imshow(X_recovered*255)
ax[1].set_title('Compressed with %d colours'%K)
ax[1].set_axis_off()

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1589510.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

基于Springboot的网上商品订单转手系统（有报告）。Javaee项目，springboot项目。

基于Springboot的网上商品订单转手系统（有报告）。Javaee项目，springboot项目。

演示视频&#xff1a; 基于Springboot的网上商品订单转手系统&#xff08;有报告&#xff09;。Javaee项目&#xff0c;springboot项目。 项目介绍&#xff1a; 采用M&#xff08;model&#xff09;V&#xff08;view&#xff09;C&#xff08;controller&#xff09;三层体系…
阅读更多...
Excel---一个工作簿中的多个sheet合并成一个PDF

Excel---一个工作簿中的多个sheet合并成一个PDF

0 Preface/Foreword 1 操作方法 1.1 方法一 文件》 导出 》创建PDF/XPS 》 选项 》发布内容 》“整个工作簿” 1.2 方法二 文件》 打印》 打印机选项中&#xff0c;选择一种PDF阅读器 》设置选项中&#xff0c;选择打印整个工作簿。
阅读更多...
二维数组中的查找

二维数组中的查找

&#x1f600;前言 在解决问题时&#xff0c;我们经常会遇到需要在二维数组中查找特定元素的情况。然而&#xff0c;如果直接使用暴力搜索&#xff0c;即遍历整个数组寻找目标元素&#xff0c;可能会导致时间复杂度较高&#xff0c;效率不高。然而&#xff0c;对于给定的二维数…
阅读更多...
代码随想录阅读笔记-回溯【分割回文串】

代码随想录阅读笔记-回溯【分割回文串】

题目 给定一个字符串 s&#xff0c;将 s 分割成一些子串&#xff0c;使每个子串都是回文串。 返回 s 所有可能的分割方案。 示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ] 思路 本题这涉及到两个关…
阅读更多...
CSS水波纹效果

CSS水波纹效果

效果图&#xff1a; 1.创建一个div <div class"point1" click"handlePoint(1)"></div> 2.设置样式 .point1{width: 1rem;height: 1rem;background: #2ce92f;position: absolute;border-radius: 50%;z-index: 999;cursor: pointer;} 3.设置伪…
阅读更多...
程序员搞副业你可以这样做

程序员搞副业你可以这样做

程序员搞副业你可以这样做 文章目录 程序员搞副业你可以这样做01/开发外包项目02/开源项目赢取打赏盈利模式之一&#xff1a;多种产品线盈利模式之二&#xff1a;技术服务型盈利模式之三&#xff1a;应用服务托管&#xff08;ASP&#xff09;盈利模式之四&#xff1a;软、硬件一…
阅读更多...
BUUCTF-Misc(1~4题)

BUUCTF-Misc(1~4题)

一.签到 答案就在上面&#xff0c;输入&#xff1a;flag{buu-ctf} 二.金三胖 然后解压得到一个GIF图 大家清楚地看到闪过了两张红色的图片 方法一&#xff1a;使用GifSplitter 2.0 然后就可以在金三胖的文件夹里生成了每一帧的图片 可以看到答案是flag{he11ohongke} 方法二…
阅读更多...
Samba实现windows和Linux共享文件，环境搭建

Samba实现windows和Linux共享文件，环境搭建

​ 搭建步骤 安装sambad sudo apt-get install samba samba-common 创建samba用户和密码 此处使用 Linux 账号和密码作为 samba 的账号和密码。Linux 账号为 shelmean shelmeanmachine:[~] $ sudo smbpasswd -a shelmean New SMB password: Retype new SMB password: Add…
阅读更多...
二叉树-数据结构

二叉树-数据结构

二叉树-数据结构 二叉树是属性结构的一个重要类型。 如下图二叉树形状 二叉树特征如下&#xff1a; 1.二叉树由 n(n > 0) 个节点组成 2.如果 n 为 0&#xff0c;则为空树 3.如果 n 1&#xff0c;则只有一个节点称为根节点(root) 4.每个节点最多有两个节点&#xff0c;节…
阅读更多...
STM32学习和实践笔记（8）: 理解位带区和位带别名区

STM32学习和实践笔记（8）: 理解位带区和位带别名区

如前《STM32学习和实践笔记&#xff08;4&#xff09;: 分析和理解GPIO_InitTypeDef GPIO_InitStructure (b)&#xff08;含memory mapping图&#xff09;-CSDN博客 》中所写&#xff0c; STM32一共有4GB的地址&#xff0c;对所有的寄存器、存储器、外设等进行统一编址。 每…
阅读更多...
PostgreSQL入门到实战-第二十二弹

PostgreSQL入门到实战-第二十二弹

PostgreSQL入门到实战 PostgreSQL中表连接操作(六)官网地址PostgreSQL概述PostgreSQL中self-join命令理论PostgreSQL中self-join命令实战更新计划 PostgreSQL中表连接操作(六) 使用PostgreSQL自联接技术来比较同一表中的行 官网地址 声明: 由于操作系统, 版本更新等原因, 文…
阅读更多...
19、矩阵-螺旋矩阵

19、矩阵-螺旋矩阵

思路: 这道题主要是对空间上有所思考&#xff0c;每次转一圈上右下左各减少一层。不妨设top&#xff0c;right&#xff0c;down&#xff0c;left&#xff0c;每次旋转一圈 top&#xff0c;right--&#xff0c;down--&#xff0c;left 代码如下&#xff1a; class Solution …
阅读更多...
【Linux】网络基础（一）

【Linux】网络基础（一）

文章目录 一、计算机网络背景1. 网络发展2. 认识“协议” 二、网络协议初识1. 协议分层2. OSI七层模型3. TCP/IP五层&#xff08;或四层&#xff09;模型 三、网络传输基本流程1. 同局域网的两台主机通信数据包封装和分用封装分用 2. 跨网络的两台主机通信 四、网络中的地址管理…
阅读更多...
应该如何进行POC测试？—【DBA从入门到实践】第三期

应该如何进行POC测试？—【DBA从入门到实践】第三期

在数据库选型过程中&#xff0c;为确保能够灵活应对数据规模的不断扩大和处理需求的日益复杂化&#xff0c;企业和技术人员会借助POC测试来评估不同数据库系统的性能。在测试过程中&#xff0c;性能、并发处理能力、存储成本以及高可用性等核心要素通常会成为大家关注的焦点&am…
阅读更多...
KNN分类算法的MATLAB实现以及可视化

KNN分类算法的MATLAB实现以及可视化

一、KNN简介 KNN算法&#xff0c;即K-Nearest Neighbors&#xff0c;是一种常用的监督学习算法&#xff0c;可以用于分类问题&#xff0c;并且在实际应用中取得了广泛的成功。 二、KNN算法的基本原理 对于给定的测试样本&#xff0c;KNN算法首先计算它与训练集中所有样本的距…
阅读更多...
电子元器件线上交易商城搭建的价值和必要性-加速度jsudo

电子元器件线上交易商城搭建的价值和必要性-加速度jsudo

随着科技的飞速发展&#xff0c;电子元器件行业正迎来前所未有的变革。为了满足市场对于电子元器件采购的便捷性、高效性和多样性的需求&#xff0c;电子元器件商城的开发显得尤为重要。本文将探讨电子元器件商城开发的重要性、主要功能以及它如何助力行业发展。 电子元器件商城…
阅读更多...
Open CASCADE学习|BrepOffsetAPI_ThruSections无法放样成Solid

Open CASCADE学习|BrepOffsetAPI_ThruSections无法放样成Solid

目录 1、边界线&#xff08;TopoDS_Wire&#xff09;不在一个平面上时&#xff0c;无法生成Solid 2、边界线&#xff08;TopoDS_Wire&#xff09;在一个平面上时&#xff0c;可以生成Solid 3、边界线&#xff08;TopoDS_Wire&#xff09;不在一个平面上时&#xff0c;添加To…
阅读更多...
每日OJ题_01背包①_牛客DP41 【模板】01背包（滚动数组优化）

每日OJ题_01背包①_牛客DP41 【模板】01背包（滚动数组优化）

目录 牛客DP41 【模板】01背包 问题一解析 问题二解析 解析代码 滚动数组优化代码 牛客DP41 【模板】01背包 【模板】01背包_牛客题霸_牛客网 #include <iostream> using namespace std;int main() {int a, b;while (cin >> a >> b) { // 注意 while 处…
阅读更多...
力扣刷题 二叉树层序遍历相关题目II

力扣刷题 二叉树层序遍历相关题目II

NO.116 填充每个节点的下一个右侧节点指针 给定一个 完美二叉树 &#xff0c;其所有叶子节点都在同一层&#xff0c;每个父节点都有两个子节点。二叉树定义如下&#xff1a; struct Node {int val;Node *left;Node *right;Node *next; } 填充它的每个 next 指针&#xff0c;…
阅读更多...
《疯狂java讲义》Java AWT图形化编程中文显示

《疯狂java讲义》Java AWT图形化编程中文显示

《疯狂java讲义》第六版第十一章AWT中文没有办法显示问题解决 VM Options设置为-Dfile.encodinggbk 需要增加变量 或者这边直接设置gbk 此外如果用swing 就不会产生这个问题了。
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023