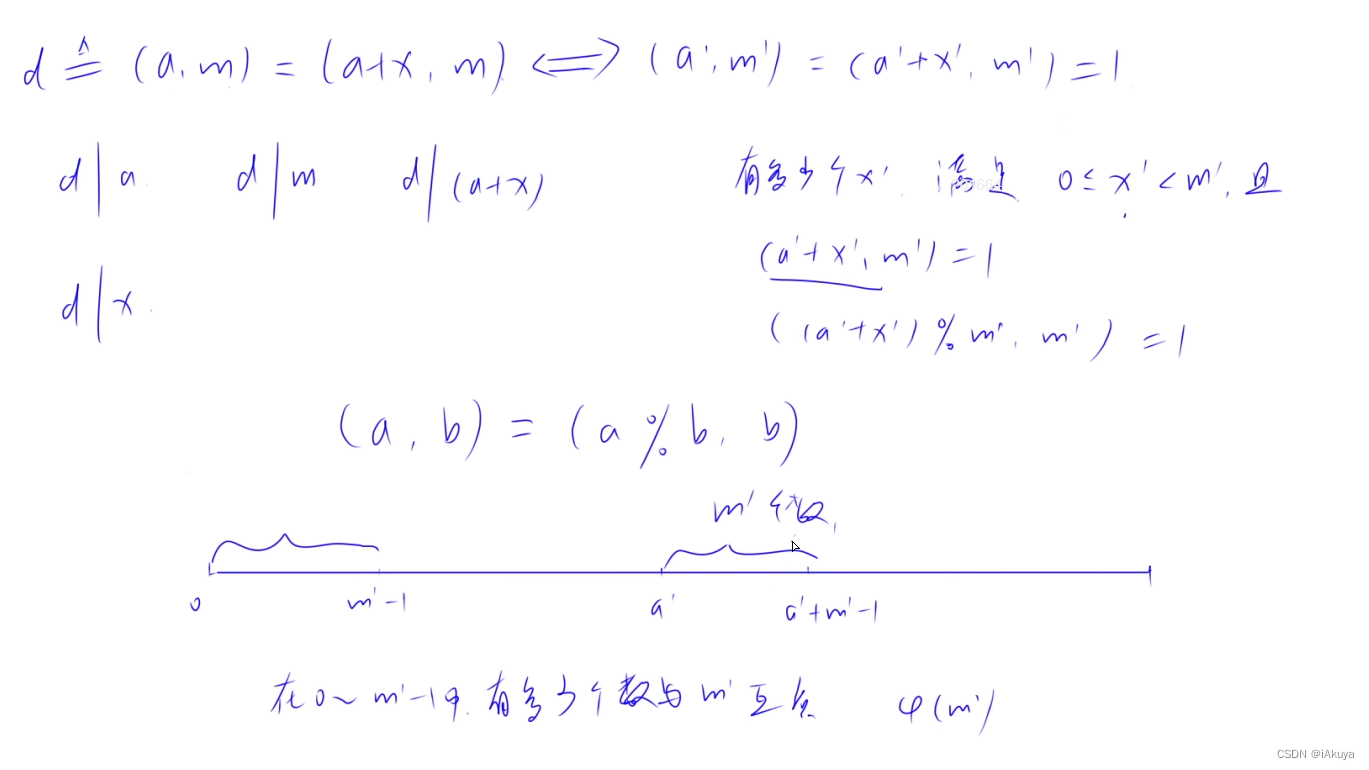题解

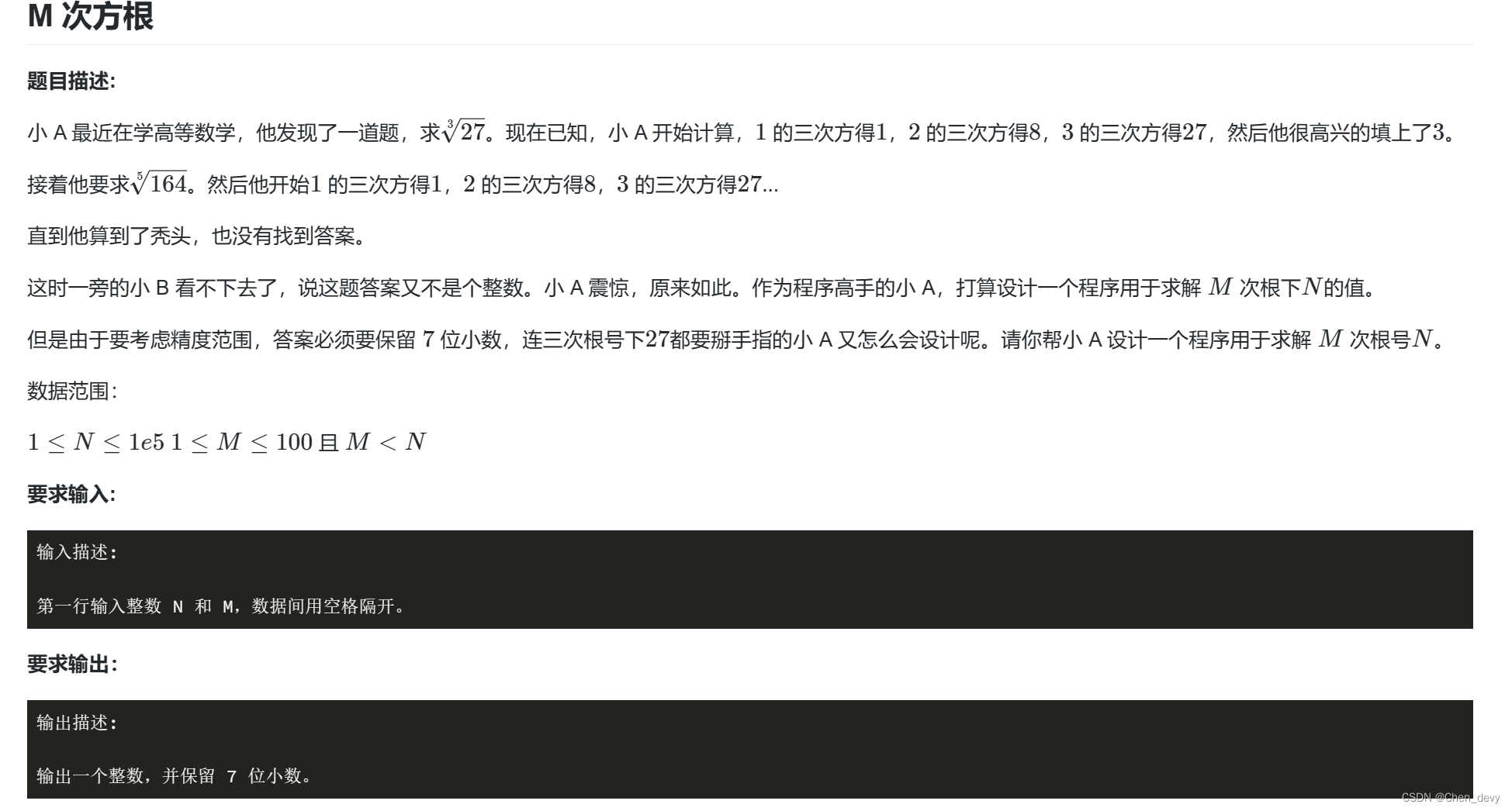
给定两个正整数 a,m，其中 a<m。

请你计算，有多少个小于 m 的非负整数 x满足：

gcd(a,m)=gcd(a+x,m)

输入格式

第一行包含整数 T ，表示共有 T 组测试数据。

每组数据占一行，包含两个整数 a,m 。

输出格式

每组数据输出一行结果，一个整数，表示满足条件的非负整数 x 的个数。

数据范围

前三个测试点满足，1≤T≤10 。 所有测试点满足，1≤T≤50 ，1≤a<m≤1010 。

• 输入样例：

3
4 9
5 10
42 9999999967

• 输出样例：

6
1
9999999966

题解

import java.util.Scanner;

/**
 * @author akuya
 * @create 2024-04-12-18:42
 */
public class GCDivisor {
    static int T;
    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        T=scanner.nextInt();
        while(T--!=0){
            long a=scanner.nextLong();
            long  b=scanner.nextLong();
            long t=gcd(a,b);
            System.out.println(phi(b/t));

        }

    }

    public static long gcd(long a,long b){
        return b==0?a:gcd(b,a%b);
    }

//欧拉函数
    public static long phi(long m){
        long res=m;
        for(long i=2;i<=m/i;i++){
            if(m%i==0){
                while(m%i==0)m/=i;
                res=res/i*(i-1);
            }
        }

        if(m>1) res=res/m*(m-1);
        return res;
    }
}

思路

这道题其实就是考察数学推理，没有什么思路，根据推理我们得出，该题的结果为1-m所有与m互质的数，那么可以通过欧拉函数直接求解。
至于欧拉函数为什么这样写，不要问，直接背，理解一次之后也会忘。当然你是大佬可以看y总基础课中的视频详细了解欧拉函数。

推导过程如下图