（Java）数据结构——图（第七节）Folyd实现多源最短路径

news2024/11/24 2:40:50

前言

本博客是博主用于复习数据结构以及算法的博客，如果疏忽出现错误，还望各位指正。

Folyd实现原理

中心点的概念

感觉像是充当一个桥梁的作用

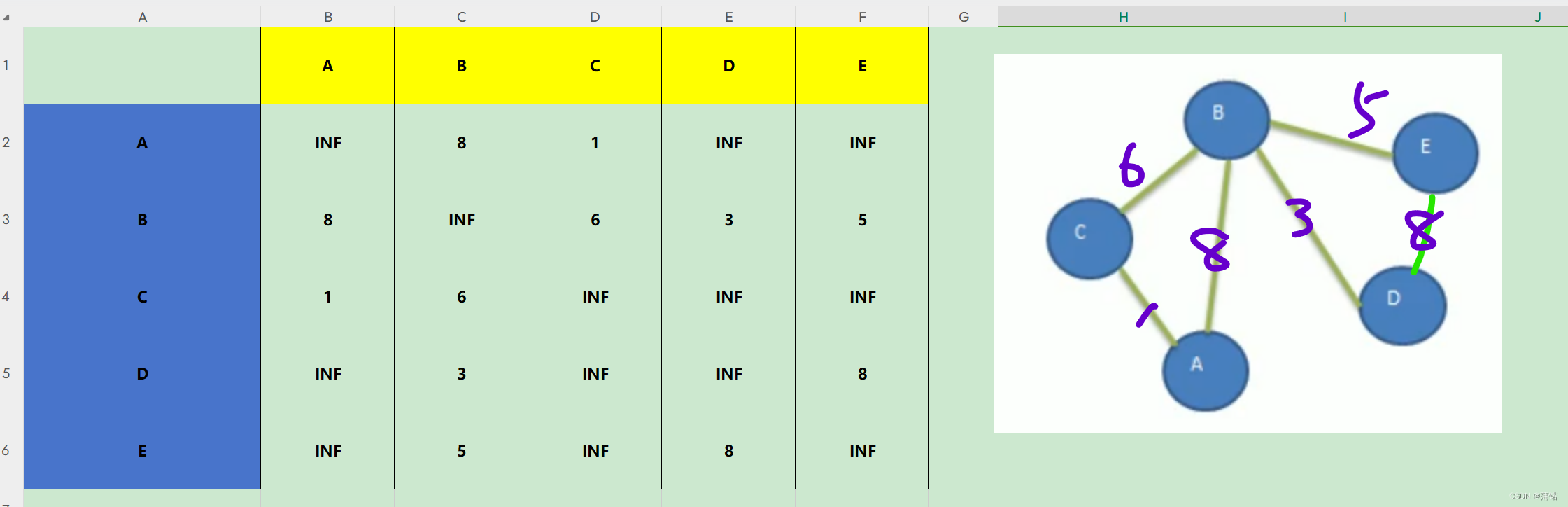
还是这个图

我们常在一些讲解视频中看到，就比如dist（-1），这是原始的邻接矩阵

dist（0），就是A充当中心点

这时候就是打比方，我D->E，A作为中心点之后，这一轮就是看D->A->E的距离相较之前是否最小，所以，A->A->B多次一举，所以pass，X->A->A也是多此一举，所以pass，对角线别动X->A->X又回到自己PASS。一来三个pass，差不多如图。我们只需要剩下的就可以。

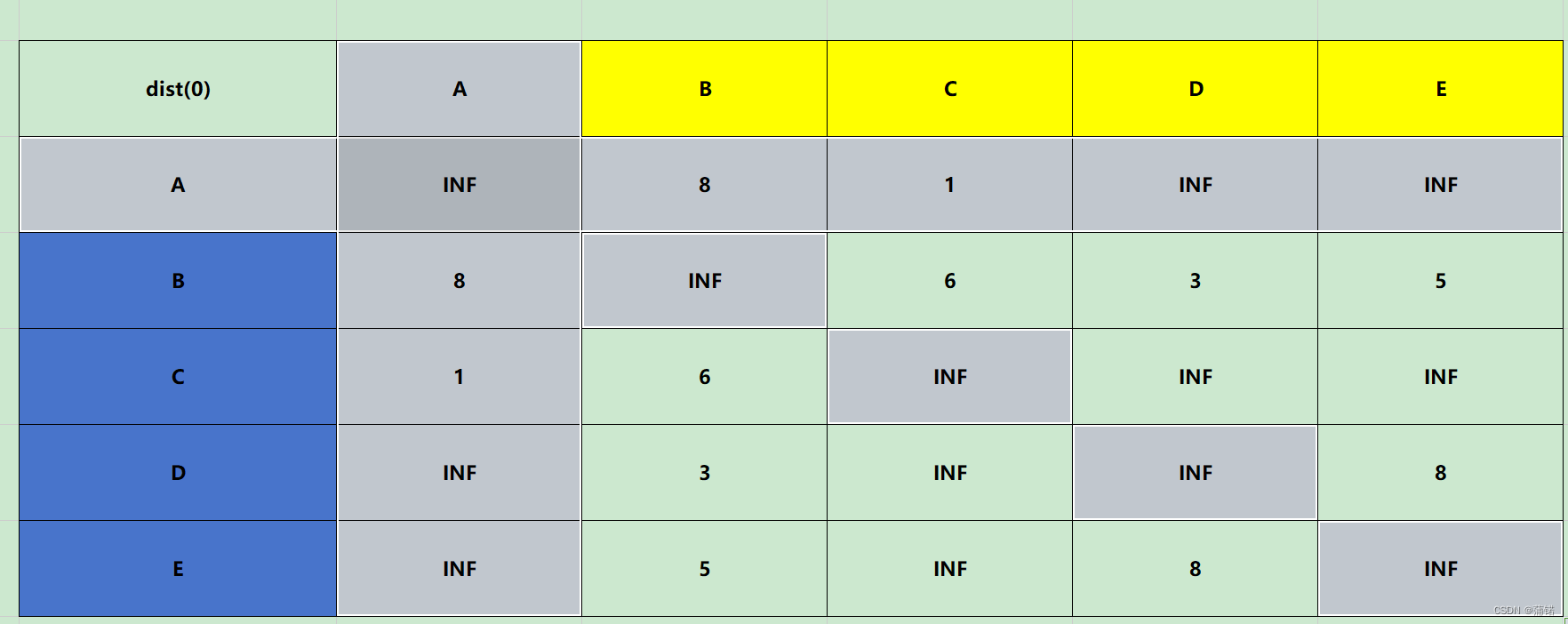
打比方B->C，那么加入A之后就是B->A->C=BA+AC=8+1=9，相比于之前的6，大了，所以不换不更新。

B->E，那么加入A之后就是B->A->E，BA+AE=8+INF，直接pass遇到不通的情况。

遍历完B，到C继续重复步骤更新……即可，脑力有限，就不多解释了。

这样我每个点都充当一次中心点下来，我的最短路径也出来了。

Folyd实现代码

Folyd的代码形式十分简单，如果比赛中看寻找最短路径，嫌Dijkstra算法麻烦的话，直接试试Folyd看看能不能过，不能再说单源的。以下是主要实现代码。

public int[][] Folyd(){
        int N = vertexList.size();
        int[][] edges = new int[N][N];
        //新开个二维数组，防止数据被动
        //edges[i] = this.edges[i]，这样是不行的，因为java的引用
        for(int i = 0;i<N;i++){
            for(int j=0;j<N;j++){
                edges[i][j] = this.edges[i][j];
            }
        }
        //弗洛伊德算法就是要求整个的
        for(int k = 0;k<N;k++){//中心点
            for(int i = 0;i<N;i++){//哪个点
                //if(i==k) continue;
                for(int j = 0;j<N;j++){//到哪个点
                    //if(j == k) continue;
                    if(i == j) continue;
                    if(edges[i][k] !=Integer.MAX_VALUE && edges[k][j] != Integer.MAX_VALUE){
                        edges[i][j] = Math.min(edges[i][j], edges[i][k] + edges[k][j]);
                        //当前的ij位置
                    }
                }
            }
        }
        return edges;
    }

三层循环，代码中注释//掉的if就是我原理里面pass的东西。

以下是完整的实现代码，以及与迪杰斯特拉算法结果的比对。

//package GraphTest.Demo;

import java.util.*;

public class Graph{//这是一个图类
    /***基础属性***/
    int[][] edges;    //邻接矩阵存储边
    ArrayList<EData> to = new ArrayList<>();    //EData包含start,end,weight三个属性，相当于另一种存储方式，主要是为了实现kruskal算法定义的
    ArrayList<String> vertexList = new ArrayList<>();    //存储结点名称，当然你若想用Integer也可以，这个是我自己复习用的
    int numOfEdges;    //边的个数
    boolean[] isVisited;
    //构造器
    Graph(int n){
        this.edges = new int[n][n];
        //为了方便，决定讲结点初始化为INF，这也方便后续某些操作
        int INF = Integer.MAX_VALUE;
        for(int i=0;i<n;i++){
            Arrays.fill(edges[i],INF);
        }
        this.numOfEdges = 0;
        this.isVisited = new boolean[n];
    }
    //插入点
    public void insertVertex(String vertex){//看自己个人喜好，我这边是一个一个在主方法里插入点的名称
        vertexList.add(vertex);
    }
    //点的个数
    public int getNumOfVertex(){
        return vertexList.size();
    }
    //获取第i个节点的名称
    public String getVertexByIndex(int i){
        return vertexList.get(i);
    }
    //获取该节点的下标
    public int getIndexOfVertex(String vertex){
        return vertexList.indexOf(vertex);
    }
    //插入边
    public void insertEdge(int v1,int v2,int weight){
        //注意，这里是无向图
        edges[v1][v2] = weight;
        edges[v2][v1] = weight;
        this.numOfEdges++;
        //如果要用Kruskal算法的话这里+
        to.add(new EData(v1,v2,weight));    //加入from to这种存储方式
    }
    //边的个数
    public int getNumOfEdge(){
        return this.numOfEdges;
    }
    //得到点到点的权值
    public int getWeight(int v1,int v2){//获取v1和v2边的权重
        return edges[v1][v2];
    }
    //打印图
    public void showGraph(){
        for(int[] line:edges){
            System.out.println(Arrays.toString(line));
        }
    }
    //获取index行 第一个邻接结点
    public int getFirstNeighbor(int index){
        for(int i = 0;i < vertexList.size();i++){
            if(edges[index][i] != Integer.MAX_VALUE){
                return i;    //找到就返回邻接结点的坐标
            }
        }
        return -1;    //没找到的话，返回-1
    }
    //获取row行 column列之后的第一个邻接结点
    public int getNextNeighbor(int row,int column){
        for(int i = column + 1;i < vertexList.size();i++){
            if(edges[row][i] != Integer.MAX_VALUE){
                return i;    //找到就返回邻接结点的坐标
            }
        }
        return -1;    //没找到的话，返回-1
    }
    //DFS实现，先定义一个isVisited布尔数组确认该点是否遍历过

    public void DFS(int index,boolean[] isVisited){
        System.out.print(getVertexByIndex(index)+" ");    //打印当前结点
        isVisited[index] = true;
        //查找index的第一个邻接结点f
        int f = getFirstNeighbor(index);
        //
        while(f != -1){//说明有
            if(!isVisited[f]){//f没被访问过
                DFS(f,isVisited);    //就进入该节点f进行遍历
            }
            //如果f已经被访问过,从当前 i 行的 f列 处往后找
            f = getNextNeighbor(index,f);
        }
    }
    //考虑到连通分量，需要对所有结点进行一次遍历，因为有Visited，所以不用考虑冲突情况
    public void DFS(){
        for(int i=0;i<vertexList.size();i++){
            if(!isVisited[i]){
                DFS(i,isVisited);
            }
        }
    }

    public void BFS(int index,boolean[] isVisited){
        //BFS是由队列实现的，所以我们先创建一个队列
        LinkedList<Integer> queue = new LinkedList<>();
        System.out.print(getVertexByIndex(index)+" ");    //打印当前结点
        isVisited[index] =true;    //遍历标志ture
        queue.addLast(index);    //队尾加入元素
        int cur,neighbor;    //队列头节点cur和邻接结点neighbor
        while(!queue.isEmpty()){//如果队列不为空的话，就一直进行下去
            //取出队列头结点下标
            cur = queue.removeFirst();    //可以用作出队
            //得到第一个邻接结点的下标
            neighbor = getFirstNeighbor(cur);
            //之后遍历下一个
            while(neighbor != -1){//邻接结点存在
                //是否访问过
                if(!isVisited[neighbor]){
                    System.out.print(getVertexByIndex(neighbor)+" ");
                    isVisited[neighbor] = true;
                    queue.addLast(neighbor);
                }
                //在cur行找neighbor列之后的下一个邻接结点
                neighbor = getNextNeighbor(cur,neighbor);
            }
        }
    }
    //考虑到连通分量，需要对所有结点进行一次遍历，因为有Visited，所以不用考虑冲突情况
    public void BFS(){
        for(int i=0;i<vertexList.size();i++){
            if(!isVisited[i]){
                BFS(i,isVisited);
            }
        }
    }

    public  void prim(int begin){
        //Prim原理：从当前集合选出权重最小的邻接结点加入集合，构成新的集合，重复步骤，直到N-1条边
        int N = vertexList.size();
        //当前的集合 与其他邻接结点的最小值
        int[] lowcost = edges[begin];
        //记录该结点是从哪个邻接结点过来的
        int[] adjvex = new int[N];
        Arrays.fill(adjvex,begin);
        //表示已经遍历过了,isVisited置true
        isVisited[begin] = true;

        for(int i =0;i<N-1;i++){//进行N-1次即可，因为只需要联通N-1条边
            //寻找当前集合最小权重邻接结点的操作
            int index = 0;
            int mincost = Integer.MAX_VALUE;
            for(int j = 0;j<N;j++){
                if(isVisited[j]) continue;
                if(lowcost[j] < mincost){//寻找当前松弛点
                    mincost = lowcost[j];
                    index = j;
                }
            }
            System.out.println("选择节点"+index+"权重为："+mincost);
            isVisited[index] = true;
            System.out.println(index);
            //加入集合后更新的操作，看最小邻接结点是否更改
            for(int k = 0;k<N;k++){
                if(isVisited[k]) continue;//如果遍历过就跳过
                if(edges[index][k] < lowcost[k]){ //加入新的节点之后更新,检查原图的index节点，加入后，是否有更新的
                    lowcost[k] = (edges[index][k]);
                    adjvex[k] = index;
                }
            }
        }
    }
    //用于对之前定义的to进行排序
    public void toSort(){
        Collections.sort(this.to, new Comparator<EData>() {
            @Override
            public int compare(EData o1, EData o2) {
                //顺序对就是升序，顺序不对就是降序，比如我现在是o1和o2传进来，比较时候o1在前就是升序，o1在后就是降序
                int result = Integer.compare(o1.weight,o2.weight);
                return result;
            }
        });
    }
    //并查集查找
    public int find(int x,int[] f){
        while(x!=f[x]){
            x = f[x];
        }
        return x;
    }
    //并查集合并
    public int union(int x,int y,int[] f){
        find(x,f);
        find(y,f);
        if(x!=y){
            f[x] = y;
            return y;
        }
        return -1;    //如果一样的集合就返回-1
    }
    public  ArrayList<Integer> kruskal(){
        //kruskal是对form to weight这种结构的类进行排序，然后选取最短的一条边，看是否形成回路，加入
        toSort();    //调用toSort进行排序
        //由于要判断是否形成回路，我们可以用DFS或者BFS，因为之前都写过，所以我们在这用并查集
        //初始化并查集
        int[] f = new int[vertexList.size()];
        for(int i = 0;i<vertexList.size();i++){
            f[i] = i;
        }
        ArrayList<Integer> res = new ArrayList<>();
        int count = 0;
        for(int i = 0;count != vertexList.size()-1 && i<this.to.size();i++){
            //之后就是开始取边了
            EData temp = this.to.get(i);
            if(union(temp.start,temp.end,f)!=-1){//如果查到不是一个集，就可以添加
                //这里都加进来是方便看哪个边
                res.add(temp.start);
                res.add(temp.end);
                count++;
            }
        }
        return res;    //最后把集合返回去就行
    }
    public int[] Dijkstra(int begin){
        int N = vertexList.size();
        //到其他点的最短路径，动态更新，直到最后返回
        int[] dist = new int[N];
        for(int i=0;i<N;i++){ //进行一下拷贝，以免更改核心数据
            dist[i] = edges[begin][i];
        }
        //System.out.println(Arrays.toString(dist));
        isVisited[begin] = true;    //该点已经遍历过
        int[] path = new int[N];    //记录这个点从哪来的，到时候在path里寻找就行
        //比如path 2 1 1 1 1，那么A就是从C来的，然后去C，C是从B来的，B是从B来的，OK结束，路径出来
        Arrays.fill(path,begin);
        for(int i = 0;i<N;i++){//几个点遍历多少次
            int min = Integer.MAX_VALUE;
            int index = 0;
            for(int j = 0;j<N;j++){//寻找当前的最短路径
                if(!isVisited[j]){
                    if(dist[j] < min){
                        min = dist[j];
                        index = j;
                    }
                }
            }
            isVisited[index] = true;    //置为遍历过
            for(int k = 0;k<N;k++){//新加入点后，看min+edges[新加点的那一行]，看是不是比以前的小，小就换了
                if(!isVisited[k] && edges[index][k]!=Integer.MAX_VALUE){//此处格外注意，因为Integer.MAX_VALUE再+就变成负的了，所以一定要注意
                    if(dist[index]+edges[index][k] < dist[k]){
                        dist[k] = dist[index]+edges[index][k];
                        path[k] = index;
                    }
                }
            }
            //找到了之后呢
        }
        //System.out.println(Arrays.toString(dist));
        //System.out.println(Arrays.toString(path));
        return dist;     //返回的是到每个点的最小路径
    }
    
    public int[][] Folyd(){
        int N = vertexList.size();
        int[][] edges = new int[N][N];
        for(int i = 0;i<N;i++){
            for(int j = 0;j<N;j++){
                edges[i][j] = this.edges[i][j];
            }
        }
        //弗洛伊德算法就是要求整个的
        for(int k = 0;k<N;k++){//中心点
            for(int i = 0;i<N;i++){//哪个点
                //if(i==k) continue;
                for(int j = 0;j<N;j++){//到哪个点
                    //if(j == k) continue;
                    if(i == j) continue;
                    if(edges[i][k] !=Integer.MAX_VALUE && edges[k][j] != Integer.MAX_VALUE){
                        edges[i][j] = Math.min(edges[i][j], edges[i][k] + edges[k][j]);
                        //当前的ij位置
                    }
                }
            }
        }
        return edges;
    }

    public static void main(String[] args) {
        int n = 5;
        String[] Vertexs ={"A","B","C","D","E"};
        //创建图对象
        Graph graph = new Graph(n);
        for(String value:Vertexs){
            graph.insertVertex(value);
        }
        graph.insertEdge(0,1,8);
        graph.insertEdge(0,2,1);
        graph.insertEdge(1,2,6);
        graph.insertEdge(1,3,3);
        graph.insertEdge(1,4,5);
        graph.insertEdge(3,4,8);
//        graph.showGraph();
//
//        graph.DFS(1, graph.isVisited);
//        System.out.println();
//        graph.DFS();//再求求所有的，看有没有剩下的
//        System.out.println();
//        Arrays.fill(graph.isVisited,false);
//        graph.BFS(1, graph.isVisited);
//        System.out.println();
//        Arrays.fill(graph.isVisited,false);
//        graph.BFS();
//        System.out.println();
//        Arrays.fill(graph.isVisited,false);
//        graph.prim(2);
//        graph.toSort();
//        for(EData i : graph.to){
//            System.out.println(i.toString());
//        }
//        System.out.println(graph.kruskal().toString());;
//        Arrays.fill(graph.isVisited,false);
        for(int i = 0;i<graph.getNumOfVertex();i++){//每个点的到其他点的最短路径只需要遍历一遍即可，时间复杂度On3
            Arrays.fill(graph.isVisited,false);
            System.out.println(Arrays.toString(graph.Dijkstra(i)));;
        }
        for(int[] i : graph.Folyd()){
            System.out.println(Arrays.toString(i));
        }
    }
}

class EData{
    //当然，这是为了方便，直接记录结点下标，而不记录像"A"这种
    int start;
    int end;
    int weight;
    EData(int start,int end,int weight){
        this.start = start;
        this.end = end;
        this.weight = weight;
    }

    @Override
    public String toString() {
        return "EData{" +
                "start=" + start +
                ", end=" + end +
                ", weight=" + weight +
                '}';
    }
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1588542.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

bayes_opt引用失败，解决方案

bayes_opt引用失败，解决方案

bayes_opt引用失败&#xff0c;如图&#xff1a; 1.pip install bayesian-optimization报错&#xff0c;如图&#xff1a; 2.【解决方案】pip install -i https://pypi.tuna.tsinghua.edu.cn/simple bayesian-optimization
阅读更多...
【opencv】示例-detect_blob.cpp

【opencv】示例-detect_blob.cpp

// 导入所需的OpenCV头文件 #include <opencv2/core.hpp> #include <opencv2/imgproc.hpp> #include <opencv2/highgui.hpp> #include <opencv2/features2d.hpp> // 导入向量和映射容器 #include <vector> #include <map> // 导入输入输出…
阅读更多...
一文读懂传统服务器与云服务器的区别

一文读懂传统服务器与云服务器的区别

传统服务器 传统服务器一般指的是物理服务器。物理服务器是独立存在的&#xff0c;无需与其他用户共享资源&#xff0c;拥有完全管理员权限和独立IP地址&#xff0c;安全稳定性高&#xff0c;性能优越。物理服务器与通用的计算机架构类似&#xff0c;由CPU、主板、内存条、硬…
阅读更多...
区块链安全-----区块链基础

区块链安全-----区块链基础

区块链是一种全新的信息网络架构 &#xff0c;是新一代信息基础设施 &#xff0c;是新型的价值交换方式、 分布式协 同生产机制以及新型的算法经济模式的基础。 区块链技术可以集成到多个领域。 区块链的主要用途 是作为加密货币的分布式总帐。 它在银行 &#xff0c;金融 &…
阅读更多...
oracle数据库怎么查看当前登录的用户？

oracle数据库怎么查看当前登录的用户？

方法如下&#xff1a; 输入select * from dba_users; 即可。 常用语句&#xff1a; 一&#xff0c;查看数据库里面所有用户&#xff1a; select * from dba_users; 前提是你是有dba权限的帐号&#xff0c;如sys,system。 二&#xff0c;查看你能管理的所有用户&#xff1…
阅读更多...
react17中配置webpack：使用@代表src目录

react17中配置webpack：使用@代表src目录

在vue的项目中可以使用表示src目录&#xff0c;使用该符号表示绝对路径&#xff0c;那么在react中想要使用怎么办呢&#xff1f; 在react中使用表示src目录是需要在webpack中配置的&#xff0c;在核心模块node_modules-》react-scripts-》config-》webpack.config.js中搜索找到…
阅读更多...
python——列表（list）

python——列表（list）

概念 列表一般使用在一次性存储多个数据 语法 lst[数据1&#xff0c;数据2&#xff0c;.....]方法 #mermaid-svg-flVxgVdpSqFaZyrF {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-flVxgVdpSqFaZyrF .error-icon{…
阅读更多...
【2024最新博客美化教程重置版】一分钟教会你在博客页面中加入javascript点击出弹出文字效果!

【2024最新博客美化教程重置版】一分钟教会你在博客页面中加入javascript点击出弹出文字效果!

&#x1f680; 个人主页 极客小俊 ✍&#x1f3fb; 作者简介&#xff1a;程序猿、设计师、技术分享 &#x1f40b; 希望大家多多支持, 我们一起学习和进步&#xff01; &#x1f3c5; 欢迎评论 ❤️点赞&#x1f4ac;评论 &#x1f4c2;收藏 &#x1f4c2;加关注 我们可以在博客…
阅读更多...
利用正射影像对斜射图像进行反向投影

利用正射影像对斜射图像进行反向投影

在图像投影和映射领域，有两种类型的投影：正向投影和反向投影。正向投影涉及使用内部方向（即校准相机参数）将 3D 点（例如地面上的物体）投影到 2D 图像平面上。另一方面，向后投影是指根据 2D 图像确定地面物体的 3D 坐标的过程。 为了匹配倾斜图像和正射影像并确定相机位置…
阅读更多...
[C++][算法基础]有向图拓扑排序(拓扑)

[C++][算法基础]有向图拓扑排序(拓扑)

给定一个 n 个点 m 条边的有向图&#xff0c;点的编号是 1 到 n&#xff0c;图中可能存在重边和自环。 请输出任意一个该有向图的拓扑序列&#xff0c;如果拓扑序列不存在&#xff0c;则输出 −1。 若一个由图中所有点构成的序列 A 满足&#xff1a;对于图中的每条边 (x,y)&a…
阅读更多...
FreeAskInternet：本地AI搜索引擎，一周收获6.4K Star

FreeAskInternet：本地AI搜索引擎，一周收获6.4K Star

简介 FreeAskInternet是一个完全免费&#xff0c;私人和本地运行的搜索聚合器和答案生成使用LLM&#xff0c;无需GPU。用户可以提出一个问题&#xff0c;系统通过搜索进行多引擎搜索&#xff0c;并将搜索结果合并到ChatGPT3.5 LLM中&#xff0c;根据搜索结果生成答案。所有进程…
阅读更多...
一、OpenCvSharp环境搭建

一、OpenCvSharp环境搭建

一、Visual Studio 创建新项目 二、选择Windows窗体应用&#xff08;.NET Framework&#xff09; 直接搜索模板&#xff1a;Windows窗体应用(.NET Framework) 记得是C#哈&#xff0c;别整成VB(Visual Basic)了 PS&#xff1a;若搜索搜不到&#xff0c;直接点击安装多个工具和…
阅读更多...
C++感受4-HelloWorld中文版——认识编码

C++感受4-HelloWorld中文版——认识编码

及时了解“编码”对编写代码的影响&#xff0c;是中国程序员越早知道越好的知识点。 一分钟了解什么叫“编码”和“解码”&#xff1b;通过实际演示&#xff0c;充分理解中文Windows下&#xff0c;C源代码编码需要注意的地方&#xff1b;通过 -finput-charsetutf8 等 g 编译配置…
阅读更多...
四、Consul服务注册与发现

四、Consul服务注册与发现

一、Consul服务注册与发现 1、为什么引入 微服务所在的IP地址和端口号硬编码到订单微服务中&#xff0c;会存在非常多的问题 &#xff08;1&#xff09;如果订单微服务和支付微服务的IP地址或者端口号发生了变化&#xff0c;则支付微服务将变得不可用&#xff0c;需要同步修改…
阅读更多...
【科技】2024最新微信机器人一键部署教程

【科技】2024最新微信机器人一键部署教程

外话 话说上次写文章好像又过了几个月了…… 其实还是因为马上小升初的各种密考&#xff0c;其它地方不知道&#xff0c;反正广东这块名校基本上都得密考考进去 笔者连考几次都惨不忍睹…… 不过5月份会有一个信息技术特长生招生&#xff0c;看看能不能吧~ 正文 先说&#xff…
阅读更多...
新质生产力与智能制造：推动制造业转型升级的双引擎

新质生产力与智能制造：推动制造业转型升级的双引擎

引言 随着科技的不断进步和全球制造业的快速发展&#xff0c;新质生产力与智能制造成为推动制造业转型升级的关键驱动力。新质生产力强调的是以科技创新和制度创新为核心&#xff0c;通过提高生产效率和经济效益来推动经济发展。而智能制造则是利用现代信息技术&#xff0c;实现…
阅读更多...
Python | Leetcode Python题解之第24题两两交换链表中的节点

Python | Leetcode Python题解之第24题两两交换链表中的节点

题目&#xff1a; 题解&#xff1a; class Solution:def swapPairs(self, head: ListNode) -> ListNode:dummyHead ListNode(0)dummyHead.next headtemp dummyHeadwhile temp.next and temp.next.next:node1 temp.nextnode2 temp.next.nexttemp.next node2node1.next…
阅读更多...
【稳定检索|投稿优惠】2024年生物学与智能计算国际会议 (ICBIC 2024)

【稳定检索|投稿优惠】2024年生物学与智能计算国际会议 (ICBIC 2024)

2024年生物学与智能计算国际会议 (ICBIC 2024) 2024 International Conference on Biology and Intelligent Computing 【会议简介】 2024年生物学与智能计算国际会议即将在上海召开。本次会议旨在汇聚生物学与智能计算领域的专家学者&#xff0c;共同探讨两者交叉融合的前沿…
阅读更多...
一文带你搞懂软件开发/怎么开发?哪些常见陷阱?如何避坑?

一文带你搞懂软件开发/怎么开发?哪些常见陷阱?如何避坑?

引言 在当今数字化时代&#xff0c;软件开发已成为推动科技进步和商业发展的重要引擎。然而&#xff0c;软件开发并非一帆风顺&#xff0c;其中蕴藏着许多陷阱和挑战。如何避免这些陷阱&#xff0c;提高软件开发的效率和质量&#xff0c;成为开发者们面临的重要问题 本文将深入…
阅读更多...
关于Ansible的模块 ⑦

关于Ansible的模块 ⑦

转载说明&#xff1a;如果您喜欢这篇文章并打算转载它&#xff0c;请私信作者取得授权。感谢您喜爱本文&#xff0c;请文明转载&#xff0c;谢谢。 在继《关于Ansible的模块 ①》、《关于Ansible的模块 ②》、《关于Ansible的模块 ③》与《关于Ansible的模块 ④》、《关于ansib…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023