一、树形DP的概念

  树形动态规划（Tree DP） 是动态规划在树结构数据上的应用。树是一种特殊的图，具有无环的特点，这使得树形动态规划在很多问题中比普通的动态规划更为直观和高效。在树形DP问题中，通常需要处理与节点相关的状态，并利用树的层次结构，自底向上或自顶向下递归地解决问题。树形DP的学习对线性DP的状态定义也有很大帮助。

1.基本概念

• 状态表示：树形DP的状态通常与树的节点相关联，每个状态代表了以某节点为根的子树在某种条件下的最优解、计数或其他性质。
• 状态转移：状态的转移依赖于子节点到父节点（或父节点到子节点）的关系。通常，要解决一个节点的问题，需要先解决它的所有子节点的问题，然后根据子节点的解来更新当前节点的解。或者当前结点的状态由父亲转移而来。

  在树形DP中，如果当前结点的状态由其子节点转移而来，那么可以进行DFS后序遍历，或者拓扑排序顺序遍历（在图中）。比如在关键路径中，提到过，求最长路径可以使用拓扑排序+动态规划来求解，这实际上就很像是一个树形DP。

2.解题步骤

  我们说树形DP的状态转移，实际上比线性DP更直观，因为父子结点之间的关系是很明显的，是从上到下的状态转移还是从下依次往下的状态转移是很明显的。

1. 定义状态：首先明确每个状态所代表的含义，以及解题需要考虑的所有情况。
2. 状态转移方程：根据问题的具体条件，找出不同状态之间的关系，形成状态转移方程。这通常涉及对当前节点的处理和对子节点状态的汇总。
3. 初始化：确定递归的基本情况，即最简单情况下各状态的值，用于终止递归。
4. 计算顺序：确定状态计算的顺序。在树形DP中，通常需要后序遍历（先处理所有子节点，再处理父节点）来自底向上计算，或者先序遍历来自顶向下传递信息。
5. 答案提取：根据定义的状态，从根节点或特定节点提取最终答案。

3.树形DP数据结构

线性dp直接可以使用线性数组来存储状态，那么树形DP怎么办呢？

• 如果真的只跟其亲儿子有关，你可以直接在树上进行DFS后序，利用DFS函数中存储状态，因为这不涉及到记忆化搜索
• 如果其不仅仅跟其亲儿子有关，你就必须采取一定行动来保存状态信息了（属于一种记忆化搜索）。
• 你可以先进行一次DFS对树结点编号（或已经有编号），然后再操作。这样你就可以定义dp数组了
• 你可以对树结点存储在哈希表中来存储该结点状态。这样你就可以定义dp了
• 如果需要新建图，你可以对树或图，存储其邻接表，并且每个结点多定义一个状态信息即可。若对于一个特定的顶点状态，它跟其邻接表中所有结点有关，如果其邻接表中的顶点状态已经被求出，则可以进行转移。树图不分家。vector实现邻接表
• ···

二、典型例题

1.LeetCode：337. 打家劫舍 III

模板题
337. 打家劫舍 III

  父亲最优解跟其子节点最优解有关，因此属于树状dp。由于父亲的最优解不仅跟其亲儿子有关，还跟孙子有关，因此我们在进行树状dp时，不能只DFS后序遍历返回结果，我们还得存储孙子信息，即记忆化搜索，因此我们在书写这个树状dp的时候，需要使用额外空间存储状态，比如在此题中没有给出编号，使用哈希表是最快的。
  但是以上我们所说的状态是单个状态 即 dp[root]表示以root为根的最高金额，如果我们定义的状态dp[root][0]表示不选择root时的最高金额，dp[root][1]表示选择root时的最高金额，那么我们只需要将树返回值是多个值（如结构体），就可以不用多开额外空间了~

1.1、定义状态转移方程

• dp[root][0]=max(dp[l_child][1],dp[l_child][0])+max(dp[r_child][1],dp[r_child][0]);//不被选择时
• dp[root][1]=root->val+dp[l_child][0]+dp[r_child][0];//被选择时
  • 根不被选择时，其能得到的最大金额的状态，由其儿子不被选择的最大金额状态以及其儿子被选择的最大金额状态转移而来，因为根不被选择时，其儿子可以被选也可以不被选，让根的金额最大，那么择其最大者就行。
  • 根被选择时，其能得到的最大金额的状态，由其儿子不被选择的最大金额状态转移而来。

1.2、参考代码

class Solution {
public:
	//pair::first表示不被选择时的最大值
	//pair::second表示被选择时的最大值
    pair<int,int> TreeDp(TreeNode * root){
        if(!root) return {0,0};
        pair<int,int> dp_left=TreeDp(root->left);
        pair<int,int> dp_right=TreeDp(root->right);
        pair<int,int> dp_root;
        //不被选择时
        dp_root.first=max(dp_left.first,dp_left.second)+max(dp_right.first,dp_right.second);
        //被选择时
        dp_root.second=root->val+dp_left.first+dp_right.first;
        return dp_root;
    }
    int rob(TreeNode* root) {
        pair<int,int> ans=TreeDp(root);
        return max(ans.first,ans.second);
    }
};

2.ACWing：285. 没有上司的舞会

模板题
285. 没有上司的舞会

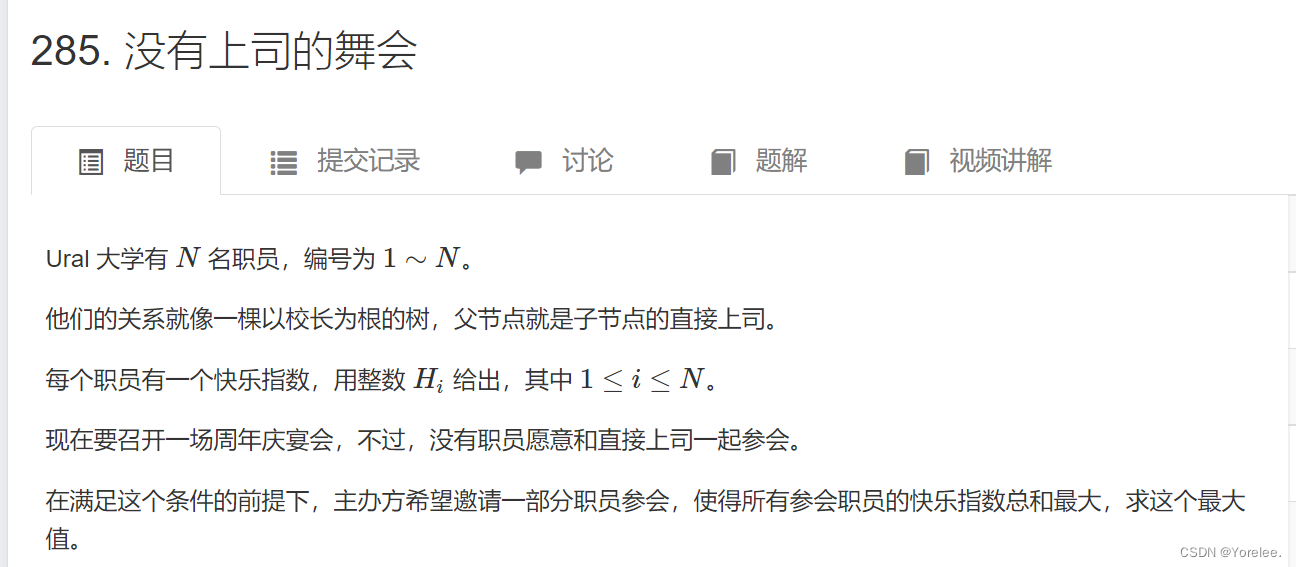
  这题和 打家劫舍 III 基本上一摸一样呀，只不过这里可能是图，并且acwing需要自己构建结点，因此这里可以提供更多建树dp思路。

没有职员愿意和直接上司一起参会。实际上就是指相邻父子结点不能同时被选择。

1.1、定义状态转移方程

  这里我们的状态和打家劫舍III的状态一模一样。不过我们可以使用拓扑排序的方式实现，只需要存储fa数组，表示父节点，因为根结点的状态由子节点转移而来，并且没必要按顺序转移~。用邻接表存图，然后按照打家劫舍III dfs实现会简单很多。

1.2、拓扑排序参考代码

#include<bits/stdc++.h>
using namespace  std;
int main(void){
    ios_base::sync_with_stdio(false);
    cin.tie(0);
    int N;
    cin>>N;
    vector<int> fa(N+1,-1);//拓扑排序方法 找寻前驱用
    vector<int> degree(N+1,0);//用于拓扑排序删除度的数组
    vector<pair<int,int>> dp(N+1);//dp状态数组,second表示被选择，first表示不被选择。
    for(int i=1;i<=N;++i) {cin>>dp[i].second;dp[i].first=0;}
    for(int i=1;i<N;++i){
        int son,Fa;
        cin>>son>>Fa;
        fa[son]=Fa;
        degree[Fa]++;
    }
    //为了和打家劫舍不一样，我们这里采用拓扑排序的方式
    //如果仍然用dfs，则需要找到根结点，dfs会方便很多，也不需要fa数组了
    stack<int> sta;
    for(int i=1;i<=N;++i){
        if(degree[i]==0){
            sta.push(i);
        }
    }
    int ans=0;
    while(!sta.empty()){
        int cur=sta.top();sta.pop();
        if(fa[cur]!=-1) {
            dp[fa[cur]].first += max(dp[cur].first, dp[cur].second);
            dp[fa[cur]].second += dp[cur].first;
            if (--degree[fa[cur]] == 0) sta.push(fa[cur]);
        }else
            ans=max(ans,max(dp[cur].first,dp[cur].second));
    }
    cout<<ans;
    return 0;
}

1.3、dfs后序遍历参考代码

#include<bits/stdc++.h>
using namespace  std;
vector<vector<int> > g;
vector<pair<int,int>> dp;//dp状态数组,second表示被选择，first表示不被选择。
void dfs(int root){
	for(int i=0;i<g[root].size();++i){
		dfs(g[root][i]);
		dp[root].second+=dp[g[root][i]].first;
		dp[root].first+=max(dp[g[root][i]].first,dp[g[root][i]].second);
	}
	return;
}
int main(void){
    ios_base::sync_with_stdio(false);
    cin.tie(0);
    int N;
    cin>>N;
    g.assign(N+1,vector<int>{});
    dp.assign(N+1,{});//dp状态数组,second表示被选择，first表示不被选择。
    unordered_set<int> roots;//用于保存根
    for(int i=1;i<=N;++i) {cin>>dp[i].second;dp[i].first=0;roots.insert(i);}
    for(int i=1;i<N;++i){
        int son,Fa;
        cin>>son>>Fa;
        g[Fa].emplace_back(son);
        roots.erase(son);
    }
    int ans=0;
    for(auto & i:roots){
		dfs(i);ans+=max(dp[i].first,dp[i].second);//从不同根遍历
	}
    cout<<ans;
    return 0;
}