一、实验目的
1.加深学生对分治法算法设计方法的基本思想、基本步骤、基本方法的理解与掌握;
2.提高学生利用课堂所学知识解决实际问题的能力;
3.提高学生综合应用所学知识解决实际问题的能力。
二、实验任务
1、最近对问题
设p1=(x1, y1), p2=(x2, y2), …, pn=(xn, yn)是平面上n个点构成的集合S,设计算法找出集合S中距离最近的点对。
(1)分别用蛮力法和分治法求解最近对问题;
(2)分析算法的时间性能,设计实验程序验证分析结论。
2、循环赛日程安排问题
设有n=2k个选手要进行网球循环赛,要求设计一个满足以下要求的比赛日程表:
(1)每个选手必须与其他n-1个选手各赛一次;
(2)每个选手一天只能赛一次。
3、排序问题
目前已知有几十种排序算法,请查找资料,并尽可能多地实现多种排序算法,并分析算法的时间复杂度。比较各种算法的优劣(冒泡排序、选择排序、插入排序、二分插入排序、希尔排序、归并排序、堆排序、快速排序等,需比较分析各种算法的时间复杂度及排序的稳定性)
4、用分治策略,设计解棋盘覆盖问题的一个简洁算法
三、实验设备及编程开发工具
编程开发工具:Microsoft Visual c++
四、实验过程设计(算法设计过程)
(一)最近对问题
1、基本算法思想
蛮力法:在蛮力法实现最近点对问题中,将问题简化:距离最近的点对可能多于一对,找出一对即可,另外只考虑二维平面中的情况。此处考虑到直接用公式计算其距离(欧几里得距离)。通过遍历所有点集,计算出每一个点对的距离,计算出最近的距离并输出。避免同一对点计算两次,只考虑i<j的点对(pi,pj)。
分治法:在利用分治法思想解决此问题时,首先考虑将最近对问题进行分治,设计其分治策略。将集合S分成两个子集S1和S2,根据平衡子问题原则,每个子集中的点数大致都为n/2。这样分治后,最近点对将会出现三种情况:在S1中,在S2中或者最近点对分别在集合S1和S2中。利用递归分析法分别计算前两种情况,第三种方法另外分析。求解出三类子情况后,再合并三类情况,比较分析后输出三者中最小的距离。
2、源程序
#include<iostream>
#include<stdio.h>
#include<stdio.h>
#include<algorithm>
#include<math.h>
#include<windows.h>
using namespace std;
struct point {
double x;
double y;
}P[100];
double distance(point p1, point p2) {
return sqrt((p1.x - p2.x)*(p1.x - p2.x) + (p1.y - p2.y)*(p1.y - p2.y));
}
bool cmp1(point p1, point p2) {
return p1.x < p2.x;
}
bool cmp2(point p1, point p2) {
return p1.y < p2.y;
}
//蛮力法
double get_min(int n)
{
double min = sqrt((P[0].x - P[1].x)*(P[0].x - P[1].x) + (P[0].y - P[1].y)*(P[0].y - P[1].y));//设置第一个计算值最短距离
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
double t = sqrt((P[i].x - P[j].x)*(P[i].x - P[j].x) + (P[i].y - P[j].y)*(P[i].y - P[j].y));
if (min>t)
min = t;
}//循环比较计算值
}
return min;
}
//分治法
double nearest_pair(point S[],int left,int right) {
cout << left << " " << right << endl;
if (right-left == 1) {
return distance(S[right], S[left]);
}
if (right - left == 2) {
double d1 = distance(S[right], S[left]);
double d2 = distance(S[right], S[right + 1]);
double d3 = distance(S[right + 1], S[left]);
d2 = min(d1, d2);
d3 = min(d2, d3);
return d3;
}
int m = (right+left) / 2;
double d1 = nearest_pair(S,left, m);
double d2 = nearest_pair(S, m+1,right);
//sort(S+right, S+left, cmp2);
double d = min(d1, d2);
int l = left, r = right;
while (S[l].x < S[m].x - d && l <= right);
l++;
while (S[r].x > S[m].x + d && r>=left)
r++;
sort(S + 1, S + r + 1, cmp2);
double d3;
for (int i = l; i <= r; i++) {
for (int j = i + 1; j <= r; j++) {
if (S[j].y - S[i].y >= d) {
break;
}
else {
d3 = distance(S[i], S[j]);
if (d3 < d)
d = d3;
}
}
}
return d;
}
int main()
{
int n;
cout << "Input n:";//设置平面中点的个数
cin >> n;
for (int i = 1; i <= n; i++) {
cout << "Input the " << i << "th number:";
cin >> P[i].x >> P[i].y;
}//逐个设置第i个点的坐标
sort(P + 1, P + n+1, cmp1);
for ( i = 1; i <= n; i++) {
cout << P[i].x << " " << P[i].y << endl;
}
double m = get_min(n);
cout <<"蛮力法结果:"<< m << endl;//蛮力法输出结果
double m2 = nearest_pair(P, 1, n);
cout <<"分治法结果:" <<m2 << endl;//分治法输出结果
system("pause");
return 0;
}
(二)循环赛日程安排问题
1、基本算法思想
假设n位选手被顺序编号为1,2,…,n,比赛的日程表是一个n行n-1列的表格,i行j列的表格内容是第i号选手在第j天的比赛对手。
根据分而治之的原则,可从其中一半选手(2^(n-1位)的比赛日程,导出全体n位选手的日程,最终细分到只有两位选手的比赛日程出发。
2、源程序
#include<stdio.h>
#include<math.h>
#define N 50
void GameTable(int k,int array[][N]);
void print(int k,int array[][N]); //输出二维数组
main()
{
int k;
int array[N][N];
printf("参赛选手的人数为n(n=2^k),请输入k 的值:");
do
{
scanf("%d",&k);
if(k>0)
{
GameTable(k,array);
print(k,array);
}
else
printf("您输入的数据有误,请重新输入");
}while(k!=0);//排除输入错误k值
}
void GameTable(int k,int array[][N])//数组下标从1开始
{
int i,j,s,t;
int n=1;
for(i=1;i<=k;i++)
n*=2; //求总人数
for(i=1;i<=n;i++)
array[1][i]=i; //第一行排1-8
int m=1; //用来控制每一次填表时i行j列的起始填充位置
for(s=1;s<=k;s++) //s指对称赋值的总循环次数,即分成几大步进行制作日程表
{
n=n/2;
for(t=1;t<=n;t++) //t指明内部对称赋值的循环次数
for(i=m+1;i<=2*m;i++)
for(j=m+1;j<=2*m;j++)
{
array[i][j+(t-1)*m*2]=array[i-m][j+(t-1)*m*2-m]; //右上角等于左上角的值
array[i][j+(t-1)*m*2-m]=array[i-m][j+(t-1)*m*2]; //左下角等于右上角的值
}
m*=2;
}
}
void print(int k,int array[][N])
{
int i,j;
int num=pow(2,k);
printf("%d人的循环赛日程表如下:\n",num);
for(i=1;i<=num;i++) //输出二维数组
{
for(j=1;j<=num;j++)
{
printf("%d\t",array[i][j]);
}
printf("\n");
}
}
(三)排序问题
(1)直接插入排序
将一个记录插入到已排序好的有序表中,从而得到一个新,记录数增1的有序表。即:先将序列的第1个记录看成是一个有序的子序列,然后从第2个记录逐个进行插入,直至整个序列有序为止。
void InsertSort(int a[], int n)
{
for(int i= 1; i<n; i++){
if(a[i] < a[i-1]){//若第i个元素大于i-1元素,直接插入。小于的话,移动有序表后插入
int j= i-1;
int x = a[i]; //复制为哨兵,即存储待排序元素
a[i] = a[i-1]; //先后移一个元素
while(x < a[j]){ //查找在有序表的插入位置
a[j+1] = a[j];
j--; //元素后移
}
a[j+1] = x; //插入到正确位置
}
print(a,n,i); //打印每趟排序的结果
}
}
(2)希尔排序
先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序,待整个序列中的记录“基本有序”时,再对全体记录进行依次直接插入排序。
void ShellInsertSort(int a[], int n, int dk)
{
for(int i= dk; i<n; ++i){
if(a[i] < a[i-dk]){ //若第i个元素大于i-1元素,直接插入。小于的话,移动有序表后插入
int j = i-dk;
int x = a[i]; //复制为哨兵,即存储待排序元素
a[i] = a[i-dk]; //首先后移一个元素
while(x < a[j]){ //查找在有序表的插入位置
a[j+dk] = a[j];
j -= dk; //元素后移
}
a[j+dk] = x; //插入到正确位置
}
print(a, n,i );
}
}
/**
* 先按增量d(n/2,n为要排序数的个数进行希尔排序
*
*/
void shellSort(int a[], int n){
int dk = n/2;
while( dk >= 1 ){
ShellInsertSort(a, n, dk);
dk = dk/2;
}
}
(3)简单选择排序
int SelectMinKey(int a[], int n, int i)
{
int k = i;
for(int j=i+1 ;j< n; ++j) {
if(a[k] > a[j]) k = j;
}
return k;
}
/**
* 选择排序
*
*/
void selectSort(int a[], int n){
int key, tmp;
for(int i = 0; i< n; ++i) {
key = SelectMinKey(a, n,i); //选择最小的元素
if(key != i){
tmp = a[i]; a[i] = a[key]; a[key] = tmp; //最小元素与第i位置元素互换
}
print(a, n , i);
}
}
(4)冒泡排序
两两比较相邻记录的关键字,如果反序则交换,直到没有反序的记录为止。
void BubbleSort(int *p, int length)
{
for (int i = 0; i < length-1; i++)
{
for (int j =length-1; j>=i;j--)
{
if (p[j-1] > p[j])
{
swap(p[j-1], p[j]);
}
}
}
}
(5)堆排序
堆排序的基本思想(利用堆,如大顶堆进行排序):将待排序的序列构造成一个大顶堆。此时,整个序列的最大值就是堆顶的根结点。将它移走(其实就是将它与堆数组的末尾元素交换,此时末尾元素就是最大值),然后将剩余n-1个序列重新构造成一个堆,这样就会得到n个元素的次小值。如此反复执行,便能得到一个有序序列。
//构造最大堆void MaxHeapFixDown(int *p, int i, int length) {
int j = 2 * i + 1;
int temp = p[i];
while (j<length) {
if (j + 1<length && p[j]<p[j + 1])
++j;
if (temp>p[j])
break;
else {
p[i] = p[j];
i = j;
j = 2 * i + 1;
}
}
p[i] = temp;
}
//堆排序void HeapSort(int *p, int length) {
for (int i = length / 2 - 1; i >= 0; i--)
{
MaxHeapFixDown(p, i, length);
}
for (int i = length - 1; i >= 1; i--)
{
swap(p[i], p[0]);
MaxHeapFixDown(p, 0, i);
cout << "i的值:" << i << " 排序:";
ergodic(p, 9);
}
}
(6)归并排序
归并排序就是利用归并思想实现的排序方法。原理:假设初始序列含有n个记录,则可以看成是n个有序的子序列,每个子序列长度为1,然后再两两归并,得到[n/2]个长度为2或1的有序子序列;再两两归并….,如此重复,直到的一个长度为n的有序序列为止,称为2路归并排序。
//将r[i…m]和r[m +1 …n]归并到辅助数组rf[i…n]
void Merge(ElemType *r,ElemType *rf, int i, int m, int n)
{
int j,k;
for(j=m+1,k=i; i<=m && j <=n ; ++k){
if(r[j] < r[i]) rf[k] = r[j++];
else rf[k] = r[i++];
}
while(i <= m) rf[k++] = r[i++];
while(j <= n) rf[k++] = r[j++];
}
void MergeSort(ElemType *r, ElemType *rf, int lenght)
{
int len = 1;
ElemType *q = r ;
ElemType *tmp ;
while(len < lenght) {
int s = len;
len = 2 * s ;
int i = 0;
while(i+ len <lenght){
Merge(q, rf, i, i+ s-1, i+ len-1 ); //对等长的两个子表合并
i = i+ len;
}
if(i + s < lenght){
Merge(q, rf, i, i+ s -1, lenght -1); //对不等长的两个子表合并
}
tmp = q; q = rf; rf = tmp; //交换q,rf,以保证下一趟归并时,仍从q 归并到rf
}
}
(7)快速排序
1)选择一个基准元素,通常选择第一个元素或者最后一个元素,
2)通过一趟排序讲待排序的记录分割成独立的两部分,其中一部分记录的元素值均比基准元素值小。另一部分记录的 元素值比基准值大。
3)此时基准元素在其排好序后的正确位置
4)然后分别对这两部分记录用同样的方法继续进行排序,直到整个序列有序
void swap(int *a, int *b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
int partition(int a[], int low, int high)
{
int privotKey = a[low]; //基准元素
while(low < high){ //从表的两端交替地向中间扫描
while(low < high && a[high] >= privotKey) --high; //从high 所指位置向前搜索,至多到low+1 位置。将比基准元素小的交换到低端
swap(&a[low], &a[high]);
while(low < high && a[low] <= privotKey ) ++low;
swap(&a[low], &a[high]);
}
print(a,10);
return low;
}
void quickSort(int a[], int low, int high){
if(low < high){
int privotLoc = partition(a, low, high); //将表一分为二
quickSort(a, low, privotLoc -1); //递归对低子表递归排序
quickSort(a, privotLoc + 1, high); //递归对高子表递归排序
}
}
(四)棋盘覆盖问题
1、基本算法原理
当k>0时,将2k×2k棋盘分割为4个2k-1×2k-1 子棋盘(a)所示。特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,从而将原问题转化为4个较小规模的棋盘覆盖问题。递归地使用这种分割,直至棋盘简化为棋盘1×1
2、源代码
//棋盘覆盖问题
/*
(tr,tc)是棋盘左上角的方格坐标
(dr,dc)是特殊方格所在的坐标
size是棋盘的行数和列数
*/
#include<iostream>
using namespace std;
int board[1025][1025];
static int tile = 1;
void ChessBoard(int tr,int tc,int dr,int dc,int size)
{
if(size==1)
return ;//递归边界
int t=tile++;//L型骨牌号
int s=size/2;//分割棋盘
//覆盖左上角子棋盘
if(dr<tr+s && dc<tc+s)
ChessBoard(tr,tc,dr,dc,s);//特殊方格在此棋盘中
else //此棋盘中无特殊方格,用t号L型骨牌覆盖右下角
{
board[tr+s-1][tc+s-1]=t;
//覆盖其余方格
ChessBoard(tr,tc,tr+s-1,tc+s-1,s);
}
//覆盖右上角子棋盘
if(dr<tr+s && dc>=tc+s)
ChessBoard(tr,tc+s,dr,dc,s);//特殊方格在此棋盘中
else //此棋盘中无特殊方格,用t号L型骨牌覆盖左下角
{
board[tr+s-1][tc+s]=t;
//覆盖其余方格
ChessBoard(tr,tc+s,tr+s-1,tc+s,s);
}
//覆盖左下角子棋盘
if(dr>=tr+s && dc<tc+s)//特殊方格在此棋盘中
ChessBoard(tr+s,tc,dr,dc,s);
else //此棋盘中无特殊方格,用t号L型骨牌覆盖右上角
{
board[tr+s][tc+s-1]=t;
//覆盖其余方格
ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
}
//覆盖右下角子棋盘
if(dr>=tr+s && dc>=tc+s)//特殊方格在此棋盘中
ChessBoard(tr+s,tc+s,dr,dc,s);
else //此棋盘中无特殊方格,用t号L型骨牌覆盖左上角
{
board[tr+s][tc+s]=t;
//覆盖其余方格
ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
}
}
int main()
{
int i,j;
int k;//棋盘大小为2^k
cout<<"棋盘大小为2^k,请输入k的值:";
while(cin>>k)
{
int size = 1<<k;
int x,y;//x,y为特殊方格的坐标
cout<<"请输入特殊方格的坐标:";
cin>>x>>y;
board[x][y]=0;
ChessBoard(0, 0, x, y, size);
for(i=0; i<size; i++)
{
for(j = 0; j < size; j++)
cout<< board[i][j]<<"\t";
cout<<"\n";
}
}
return 0;
}
五、实验结果及算法复杂度分析
(一)最近对问题
1、实验结果
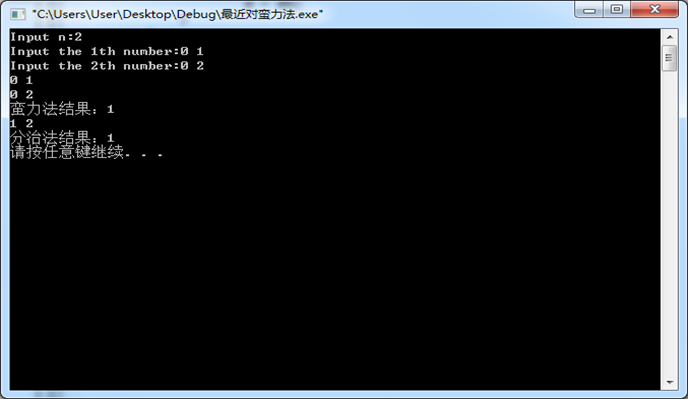
2、时间复杂度
蛮力法:O(n^2)
分治法:O(nlog2n)
(二)循环赛日程安排问题
1、实验结果
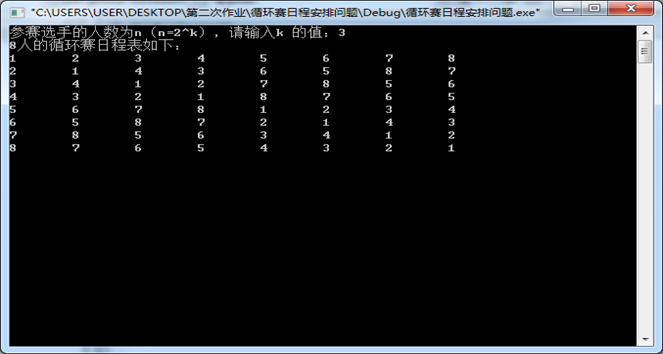
2、时间复杂度
时间复杂度:O(2^k * 2^k)
(三)排序问题
1、实验结果
1、直接插入排序
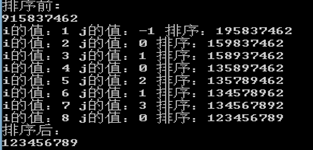
2、 希尔排序
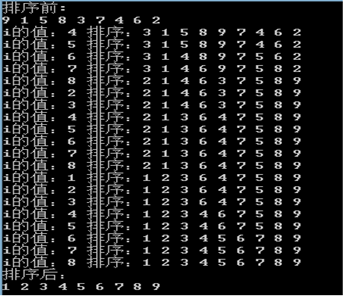
3、简单选择排序
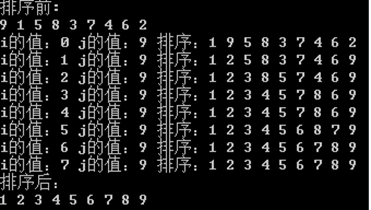
4、冒泡排序
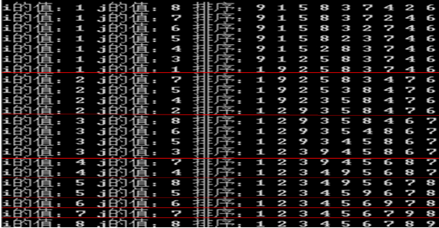
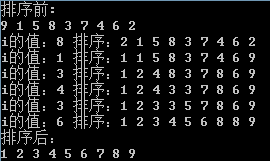
5、 堆排序
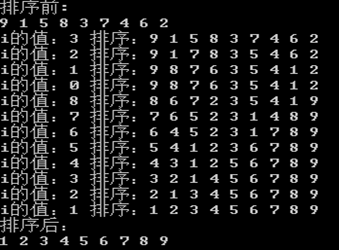
7、快速排
2、时间复杂度
1、直接插入排序时间复杂度:O(n^2);
2、 希尔排序时间复杂度:O(n^2);
3、简单选择排序时间复杂度:O(n^2);
4、冒泡排序时间复杂度:O(n^2);
5、 堆排序时间复杂度:O(nlog2n);
6、 归并排序时间复杂度:O(nlog n);
7、快速排序时间复杂度:0(n^2)。
(四)棋盘覆盖问题
1、实验结果
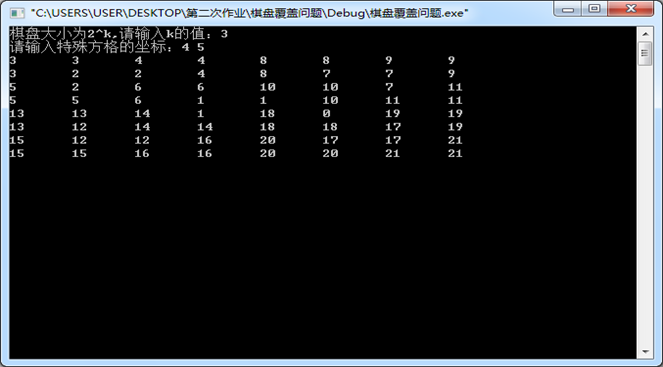
2、时间复杂度
最坏时间复杂度:O(4^k)
实验小结(包括问题和解决方法、心得体会等)
本次实验的中心思想就是分治法,在课堂教学中老师就对分治法进行了比较深刻的讲解,再加上在网上百度就对分治法有了比较清楚的认识,字面上的解释是“分而治之”,就是把一个复杂的问题分成两个或更多的相同或相似的子问题,再把子问题分成更小的子问题……直到最后子问题可以简单的直接求解,原问题的解即子问题的解的合并。在通过实验的四道题目的实践,相信自己对分治法已经足够掌握了。