前言

本博客是博主用于复习数据结构以及算法的博客，如果疏忽出现错误，还望各位指正。

AOV网

先前我们了解了有向无环图DAG的概念。

所有的工程或者某种流程可以分为若干个小的工程或者阶段，这些小的工程或者阶段就称为活动。若以图中的顶点来表示活动，有向边表示活动之间的优先关系，则这样活动在顶点上的有向图，就称为AOV图（Activity On Vertex Network）。

与AOE网的区别就是：AOE的边是活动（Activity On Edge Network），要不是今天看了下书，我就记混了。

AOV网主要是看工程是否能够顺利进行（拓扑排序判断DAG图，或者其他也行，比如DFS再次碰见isVisited[N] = true等等），AOE则是主要看工程完成所必须的最短时间（关键路径）。

拓扑排序代码实现

原理：找入度为0的，加入栈，然后出栈，遍历它的“链表”，链表里有的结点入度-1，归0后加入栈，依次往复。直到栈里空了，判断一下是不是都遍历了，或者计数也行。都遍历了就是DAG，没遍历完就不是。

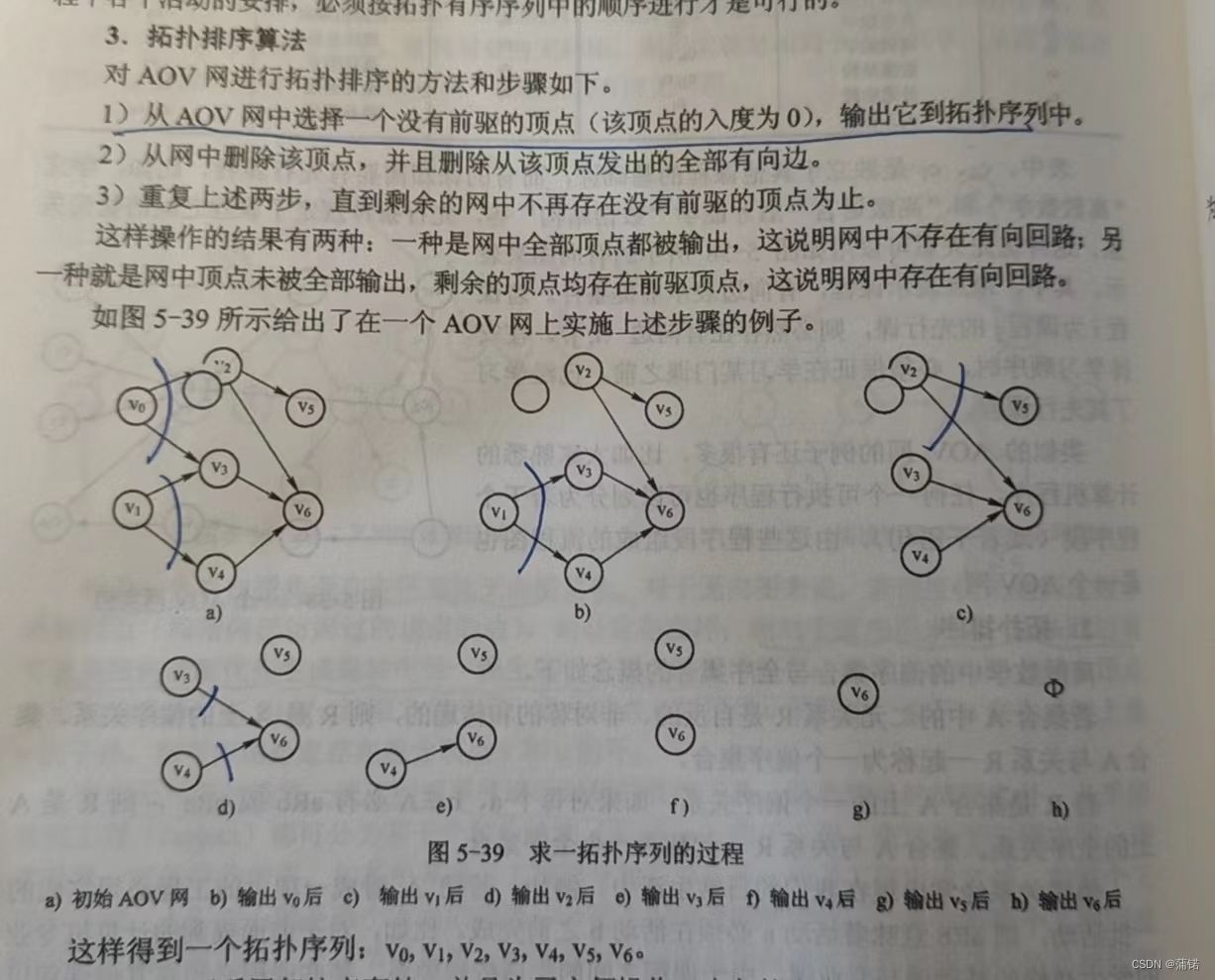
可以看我的另一篇博客，或者直接看实现。

LeetCode 207.课程表——拓扑排序&真真切切建图实现-CSDN博客

应该是没问题的实现（如果出问题，就是搬自己LeetCode时候有的变量名没改）。

package GraphTest.Demo;

import java.util.ArrayList;
import java.util.Arrays;
import java.util.LinkedList;
import java.util.Scanner;

class Test {
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        Graph graph = new Graph(numCourses);
        for(int i = 0;i<prerequisites.length;i++){
            //插入结点
            graph.insertEdge(prerequisites[i][0],prerequisites[i][1],1);
        }
        return graph.tuopu();
    }

    public static void main(String[] args) {
        //主要是接收数据麻烦点，其他没啥
        Scanner in = new Scanner(System.in);
        int numCourses = Integer.parseInt(in.nextLine());
        String[] str = in.nextLine().replaceAll("\\[","").replaceAll("]","").split(",");
        int n = str.length / 2;
        int[][] prerequisites = new int[n][2];
        for(int i = 0;i<n;i++){
            prerequisites[i][0] = Integer.parseInt(str[2*i]);
            prerequisites[i][1] = Integer.parseInt(str[2*i+1]);
            System.out.println(prerequisites[i][0]+" "+prerequisites[i][1]);
        }
        System.out.println(canFinish(numCourses,prerequisites));
    }
}

class InData{
    int in;
    int vertex;
    ArrayList<Integer> next = new ArrayList<>();
    InData(int vertex){
        this.in = 0;
        this.vertex = vertex;
    }
}


class Graph{
    int[][] edges;  //边集合
    //ArrayList<Integer> vertexList = new ArrayList<>();  
    //点集合，在这因为没有名称，都是下标，所以不用这个变量
    int numOfEdges;
    InData[] inData;
    boolean[] isVisited;
    Graph(int N){
        this.edges = new int[N][N];
        /*for(int i =0;i<N;i++){
            Arrays.fill(edges[i],Integer.MAX_VALUE);
        }
        然后我之前一弄是54ms，发现是写了好多个打印，一删掉就掉到了13ms
        然后我又发现把这个注释了就从13ms掉到了7ms
        */
        this.numOfEdges = 0;
        this.inData = new InData[N];
        for(int i = 0;i<N;i++){
            inData[i] = new InData(i);
        }
        /*for(int i = 0;i<N;i++){
            vertexList.add(i);
        }*/
        this.isVisited = new boolean[N];
    }
    public void insertEdge(int v1,int v2,int weight){
        this.edges[v1][v2] = weight;
        this.inData[v1].next.add(v2);
        this.inData[v2].in++;
    }
    public boolean tuopu(){//拓扑排序——判断是否能生成一个时间有序的序列
        //一开始我们已经在图中初始化顶点个数个InData类型组成数组，现在我们把他们拷贝过来
        LinkedList<InData> stack = new LinkedList<>();
        InData[] list = new InData[isVisited.length];
        
        for(int i = 0;i<list.length;i++){
            list[i] = inData[i];
            if(list[i].in == 0){//如果发现入度为0就加入栈中
                stack.addFirst(list[i]);
                this.isVisited[i] = true;    //进入栈中的置为已经遍历过
            }
        }
        
        while(!stack.isEmpty()){
            //得到“邻接表”
            ArrayList<Integer> temp = stack.removeFirst().next;
            for(int i:temp){
                //list对应位置的入度-1
                list[i].in--;
                if(list[i].in == 0){
                    //如果对应位置的入度在此刻变成0的话，加入栈中
                    stack.addFirst(list[i]);
                    this.isVisited[i] = true;
                }
            }
        }
        //之后进行判断，如果存在没有遍历过的，直接返回false不能生成
        for(int i = 0;i<isVisited.length;i++){
            if(!isVisited[i]){
                return false;
            }
        }
        return true;
    }
}