简介
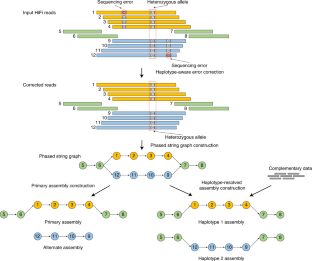
Hifiasm[1] 是一个快速的单倍型解析 de novo 组装软件,最初设计用于 PacBio HiFi 读取。其最新版本可以通过利用超长的 Oxford Nanopore 读取支持端粒到端粒的组装。Hifiasm 可以生成单样本端粒到端粒的组装,结合了 HiFi、超长和 Hi-C 读取,可以说是最好的组装软件之一。对于 trio-binning 组装来说,它是最好的单倍型解析组装软件之一,适用于父本短读取。对于人类基因组来说,hifiasm 可以在一天内完成端粒到端粒的组装。
Install
-
手动安装
git clone https://github.com/chhylp123/hifiasm
cd hifisam && make
-
conda(推荐)
conda install -c bioconda hifiasm
Usages
Notes
-
no need polish -
无需合并多个输入文件 -
绝大多数二倍体基因组,只需要组装2n中的n,所以参数一般给 -l 2 -n 4
HiFi only
-
无需额外的数据类型组装 HiFi reads
hifiasm -o NA12878.asm -t 32 NA12878.fq.gz
# no need haplotype
hifiasm --primary -o NA12878.asm -t 32 NA12878.fq.gz
# -l:0:没有对组装去冗余,组装结果包括全部组装出来的contig,可能包含多个单倍体基因组;2/3:会对组装出来的基因组进行去冗余,对于二倍体,得到的结果基本上是全基因组一半的大小
# -n: 一般给3或者4,默认3,表示组装的contig中,unitigs支持大于3或4才保留,该参数会将支持度比较低的contig去掉
ONT
-
Hifiasm 可以集成超长 ONT 读取来生成端粒到端粒的组装:
# only ONT
hifiasm -o NA12878.asm -t32 --ul ul.fq.gz HiFi-reads.fq.gz
# + Hi-C
hifiasm -o NA12878.asm -t32 --ul ul.fq.gz --h1 read1.fq.gz --h2 read2.fq.gz HiFi-reads.fq.gz
# + parental
hifiasm -o NA12878.asm -t32 --ul ul.fq.gz -1 pat.yak -2 mat.yak HiFi-reads.fq.gz
parental
-
当有父本的短读取可用时,hifiasm 还可以通过 trio binning 生成一对单倍型解析的组装。要进行这样的组装,您首先需要使用 yak 对 k-mer 进行计数,然后再进行组装。
yak count -k31 -b37 -t16 -o pat.yak paternal.fq.gz
yak count -k31 -b37 -t16 -o mat.yak maternal.fq.gz
hifiasm -o NA12878.asm -t 32 -1 pat.yak -2 mat.yak NA12878.fq.gz
Hi-C
-
利用成对的端到端 Hi-C reads 生成一对单倍型解析的组装。
hifiasm -o NA12878.asm -t32 --h1 read1.fq.gz --h2 read2.fq.gz HiFi-reads.fq.gz
Results
一般来说,hifiasm 会创建一系列的 GFA 格式的基因组组装图谱:
prefix.r_utg.gfa: 解决了单倍型问题的原始单元图谱,它详尽地记录了所有的单倍型数据。
prefix.p_utg.gfa: 经过处理的单倍型解析单元图谱,图中去除了可能由基因突变或数据噪声造成的小气泡,这些小气泡并不代表真实的单倍型信息。hifiasm 会依据测序深度自动去除这些小气泡,其中 --hom-cov 参数会影响这一处理过程的具体结果。详细信息可以参考关于同源纯合覆盖度的设置。另外,使用 -p 参数可以强制去除这些小气泡。
prefix.p_ctg.gfa: 主要连续片段的图谱,它整合了一个包含长期阶段区块的完整组装结果。
prefix.a_ctg.gfa: 包含所有在主要连续片段图谱中未被采用的连续片段的图谱。
prefix.hap.p_ctg.gfa: 带有相位信息的连续片段图谱,它保留了具有相位标记的连续片段。
-
获取组装结果
# get fasta
awk '/^S/{print ">"$2;print $3}' test.p_ctg.gfa > test.p_ctg.fa
Source: https://github.com/chhylp123/hifiasm
本文由 mdnice 多平台发布