Leetcode算法训练日记 | day20

news2025/2/28 20:21:20

一、合并二叉树

1.题目

Leetcode：第 617 题

给你两棵二叉树： root1 和 root2 。

想象一下，当你将其中一棵覆盖到另一棵之上时，两棵树上的一些节点将会重叠（而另一些不会）。你需要将这两棵树合并成一棵新二叉树。合并的规则是：如果两个节点重叠，那么将这两个节点的值相加作为合并后节点的新值；否则，不为 null 的节点将直接作为新二叉树的节点。

返回合并后的二叉树。

注意: 合并过程必须从两个树的根节点开始。

示例 1：

输入：root1 = [1,3,2,5], root2 = [2,1,3,null,4,null,7]
输出：[3,4,5,5,4,null,7]

示例 2：

输入：root1 = [1], root2 = [1,2]
输出：[2,2]

2.解题思路

首先检查两个输入树的根节点是否为空，如果其中一个为空，则返回另一个作为结果。如果两个根节点都不为空，将合并它们的值，并对它们的左右子树递归地执行合并操作。这个过程一直持续到所有节点都被合并，最终返回更新后的根节点，包含了合并后二叉树的根。

3.实现代码

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

// 定义一个结构体TreeNode，用于表示二叉树的节点。
struct TreeNode {
    int val; // 存储节点的值。
    TreeNode* left; // 指向该节点左子树的指针。
    TreeNode* right; // 指向该节点右子树的指针。
    // TreeNode的构造函数，用于创建一个TreeNode实例。
    // 参数x是节点的值，left和right默认为NULL，表示没有左右子节点。
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

// 一、合并两棵二叉树（递归法）。
class Solution1 {
public:
    // mergeTrees函数用于合并两个给定的二叉树root1和root2。
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (root1 == NULL) return root2;// 如果root1为空，则返回root2作为合并后的树的根节点。
        if (root2 == NULL) return root1; // 如果root2为空，则返回root1作为合并后的树的根节点。

        root1->val = root1->val + root2->val;// 将root1的值与root2的值相加，并将结果赋给root1，这是合并操作的一部分。
        root1->left = mergeTrees(root1->left, root2->left);// 递归调用mergeTrees函数合并root1和root2的左子树。
        root1->right = mergeTrees(root1->right, root2->right); // 递归调用mergeTrees函数合并root1和root2的右子树。

        return root1;// 返回更新后的root1作为合并后的树的根节点。
    }
};

// 二、合并两棵二叉树（迭代法法）。
class Solution2 {
public:
    // mergeTrees函数用于合并两个给定的二叉树root1和root2。
    TreeNode* mergeTrees(TreeNode* root1, TreeNode* root2) {
        if (root1 == NULL) return root2;  // 如果root1为空，直接返回root2作为合并后的树的根节点。
        if (root2 == NULL) return root1; // 如果root2为空，直接返回root1作为合并后的树的根节点。

        queue<TreeNode*> que; // 创建一个队列que，用于在合并过程中存储待处理的节点对。
        que.push(root1); // 将root1和root2入队。
        que.push(root2);

        // 使用while循环处理队列中的所有节点对。
        while (!que.empty()) {
            // 取出队列中的两个节点，node1对应root1的节点，node2对应root2的节点。
            TreeNode* node1 = que.front();
            que.pop();
            TreeNode* node2 = que.front();
            que.pop();

            node1->val = node1->val + node2->val;// 将node1和node2的值相加，并将结果赋给node1。

            // 如果node1和node2都有左子节点，将它们入队以进行后续合并。
            if (node1->left != NULL && node2->left != NULL) {
                que.push(node1->left);
                que.push(node2->left);
            }

            // 如果node1和node2都有右子节点，将它们入队以进行后续合并。
            if (node1->right != NULL && node2->right != NULL) {
                que.push(node1->right);
                que.push(node2->right);
            }

            //因为返回的是root1二叉树，只需考虑考虑root1存在空节点对应的root2不为空节点的情况
            // 而不需要考虑root1存在节点对应的root2为空节点的情况
            // 如果node1没有左子节点，但node2有左子节点，将node2的左子节点赋给node1。
            if (node1->left == NULL && node2->left != NULL) {
                node1->left = node2->left;
            }

            // 如果node1没有右子节点，但node2有右子节点，将node2的右子节点赋给node1。
            if (node1->right == NULL && node2->right != NULL) {
                node1->right = node2->right;
            }//因为返回的是root1二叉树，所以不需要考虑root1存在节点对应的root2为空节点的情况
        }

        return root1;// 由于函数只接收root1的指针，返回root1，此时它已经是合并后的树的根节点。
    }
};

二、二叉搜索树中的搜索

1.题目

Leetcode：第 700 题

给定二叉搜索树（BST）的根节点 root 和一个整数值 val。

你需要在 BST 中找到节点值等于 val 的节点。 返回以该节点为根的子树。 如果节点不存在，则返回 null 。

示例 1:

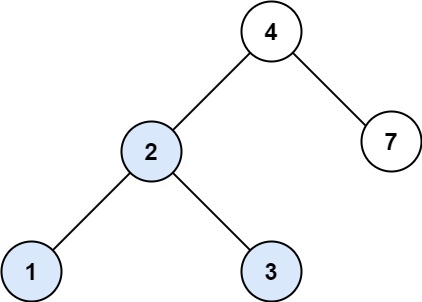
输入：root = [4,2,7,1,3], val = 2
输出：[2,1,3]

示例 2:

输入：root = [4,2,7,1,3], val = 5
输出：[]
2.解题思路

首先检查当前根节点是否为空或者是否已经找到目标值。如果当前节点为空，或者其值等于目标值，则直接返回当前节点。如果当前节点的值大于目标值，函数递归地在左子树中查找；如果当前节点的值小于目标值，则递归地在右子树中查找。最终，函数返回查找结果，如果找到了匹配的节点，则返回该节点；否则返回NULL。

3.实现代码
#include <iostream>
#include <vector>
#include <queue>
using namespace std;

// 定义一个结构体TreeNode，用于表示二叉树的节点。
struct TreeNode {
    int val; // 存储节点的值。
    TreeNode* left; // 指向该节点左子树的指针。
    TreeNode* right; // 指向该节点右子树的指针。
    // TreeNode的构造函数，用于创建一个TreeNode实例。
    // 参数x是节点的值，left和right默认为NULL，表示没有左右子节点。
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

// 一、在二叉搜索树中查找特定值的节点（递归法）。
class Solution1 {
public:
    // searchBST函数用于在二叉搜索树root中查找值为val的节点。
    TreeNode* searchBST(TreeNode* root, int val) {
        if (root == NULL || root->val == val) return root; // 如果根节点为空，或者根节点的值等于要查找的值val，返回当前节点。
        TreeNode* result = NULL;// 初始化结果指针为NULL，用于存储找到的节点。
        if (root->val > val) result = searchBST(root->left, val);// 如果根节点的值大于要查找的值val，递归搜索左子树。
        if (root->val < val) result = searchBST(root->right, val);// 如果根节点的值小于要查找的值val，递归搜索右子树。   
        return result;// 返回搜索结果，如果找到则返回找到的节点，否则返回NULL。
    }
};


// 二、在二叉搜索树中查找特定值的节点（递归法）。
class Solution2 {
public:
    // searchBST函数用于在二叉搜索树root中查找值为val的节点并返回。
    TreeNode* searchBST(TreeNode* root, int val) {
        while (root != NULL) {  // 使用while循环，当root不为NULL时继续搜索。
            if (root->val > val) {// 如果root的值大于要查找的值val，向左子树搜索。
                root = root->left;
            }
            else if (root->val < val) {// 如果root的值小于要查找的值val，向右子树搜索。
                root = root->right;
            }
            else {// 如果root的值等于要查找的值val，找到了目标节点，返回root。
                return root;
            }
        }
        return NULL; //未找到就返回NULL。
    }
};

三、验证二叉搜索树

1.题目

Leetcode：第 98 题

给你一个二叉树的根节点 root ，判断其是否是一个有效的二叉搜索树。

有效 二叉搜索树定义如下：

  • 节点的左

    子树

    只包含 小于 当前节点的数。
  • 节点的右子树只包含 大于 当前节点的数。
  • 所有左子树和右子树自身必须也是二叉搜索树。

示例 1：

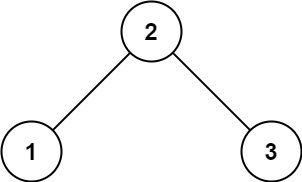
输入：root = [2,1,3]
输出：true

示例 2：

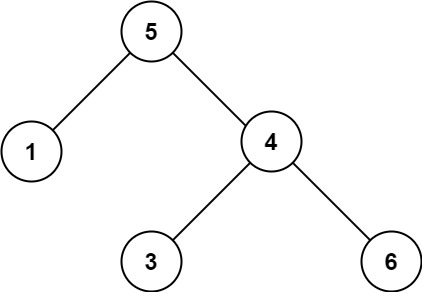
输入：root = [5,1,4,null,null,3,6]
输出：false
解释：根节点的值是 5 ，但是右子节点的值是 4 。
2.解题思路

1.一般递归法：递归遍历整个二叉树，将所有节点的元素使用vector保存，检查是否所有的元素都是严格递增的，如果不是，就说明不是一个有效的二叉搜索树。

2.双指针递归法：在递归遍历整个二叉树的过程中，用两个指针来检查是否满足每个节点的值都应该大于其左子树中所有节点的值，并且小于其右子树中所有节点的值。如果不是，就说明不是一个有效的二叉搜索树。

3.迭代法：通过使用栈 st 来存储待访问的节点，可以在每次循环中选择最左边的节点进行访问，从而模拟中序遍历的过程。同时，使用指针 pre 来记录遍历过程中的前一个节点值，以便在访问当前节点时检查其是否违反了二叉搜索树的性质。如果遍历完整棵树都没有发现违反性质的情况，则可以认为该二叉树是有效的二叉搜索树。

3.实现代码
#include <iostream>
#include <vector>
#include <stack>
using namespace std;

// 定义一个结构体TreeNode，用于表示二叉树的节点。
struct TreeNode {
    int val; // 存储节点的值。
    TreeNode* left; // 指向该节点左子树的指针。
    TreeNode* right; // 指向该节点右子树的指针。
    // TreeNode的构造函数，用于创建一个TreeNode实例。
    // 参数x是节点的值，left和right默认为NULL，表示没有左右子节点。
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

// 一、验证二叉搜索树（一般递归法）。
class Solution {
public:
    vector<int> vec; // 定义一个vec，用于存储二叉树节点的值

    // 定义一个名为traversal的成员函数，用于执行二叉树的中序遍历。
    void traversal(TreeNode* root) {
        if (root == NULL) return; // 如果当前节点为空，直接返回，不执行任何操作。
        traversal(root->left); // 递归调用traversal函数遍历当前节点的左子树。
        vec.push_back(root->val); // 访问当前节点，将其值添加到vec中。
        traversal(root->right); // 递归调用traversal函数遍历当前节点的右子树。
    }

    // 定义一个名为isValidBST的成员函数，用于验证给定的二叉树是否为有效的二叉搜索树。
    // 参数root是二叉树的根节点指针。
    bool isValidBST(TreeNode* root) {
        vec.clear(); // 清空向量vec，为新的中序遍历做准备。
        traversal(root); // 调用traversal函数，传入根节点，执行中序遍历。
        
        for (int i = 1; i < vec.size(); i++) {// 遍历向量vec，检查中序遍历的结果是否为升序。
            if (vec[i] <= vec[i - 1]) return false; // 如果发现任何违反升序的元素对，返回false。
        }
        return true; // 如果遍历完成没有发现违反升序的元素对，返回true，表明是有效的二叉搜索树。
    }
};

//二、验证二叉搜索树（双指针递归法）。
class Solution2 {
public:
    // 定义一个指向TreeNode的指针pre，初始化为NULL，用于在遍历过程中记录前一个访问的节点。
    TreeNode* pre = NULL;
    // 定义一个名为isValidBST的成员函数，用于验证给定的二叉树是否为有效的二叉搜索树。
    // 参数root是二叉树的根节点指针。
    bool isValidBST(TreeNode* root) {
        if (root == NULL) return true;  // 如果当前节点为空，说明是有效的二叉搜索树，返回true。

        // 递归调用isValidBST函数检查当前节点的左子树是否为有效的二叉搜索树。
        bool left = isValidBST(root->left);

        // 如果pre不为NULL，并且前一个访问的节点的值大于当前节点的值，说明不是有效的二叉搜索树，返回false。
        // 这是二叉搜索树的性质：每个节点的值都应该大于其左子树中所有节点的值。
        if (pre != NULL && pre->val > root->val) return false;

        pre = root; // 更新pre为当前节点，以便在递归检查右子树时使用。

        // 递归调用isValidBST函数检查当前节点的右子树是否为有效的二叉搜索树。
        bool right = isValidBST(root->right);

        // 返回左子树和右子树的检查结果，只有当左右子树都满足二叉搜索树的性质时，整个树才是有效的。
        return left && right;
    }
};

// 三、验证二叉搜索树（迭代法）。
class Solution3 {
public:
    // 定义一个成员函数isValidBST，用于验证给定的二叉树是否为有效的二叉搜索树。
    // 参数root是二叉树的根节点指针。
    bool isValidBST(TreeNode* root) {
        stack<TreeNode*> st; // 定义一个栈st，用于存放二叉树的节点指针，辅助进行迭代遍历。
        TreeNode* cur = root; // 定义一个当前节点指针cur，初始指向根节点。
        TreeNode* pre = NULL; // 定义一个前一个节点指针pre，初始为NULL，用于记录遍历过程中的前一个节点值。

        // 当当前节点不为空，或者栈st不为空时，继续遍历。
        while (cur != NULL || !st.empty()) {
            
            if (cur != NULL) {// 如果当前节点不为空，将当前节点压入栈st，并将cur更新为当前节点的左子节点。
                st.push(cur); // 将当前节点压入栈中。
                cur = cur->left; // 将cur更新为当前节点的左子节点，开始遍历左子树。
            }
            else {
                // 如果当前节点为空，从栈st中弹出一个节点作为当前节点。
                cur = st.top(); // 获取栈顶节点。
                st.pop(); // 弹出栈顶节点。

                // 如果pre不为空，并且当前节点的值小于pre记录的前一个节点的值，说明不是有效的二叉搜索树，返回false。
                // 这是二叉搜索树的性质：每个节点的值都应该大于其左子树中所有节点的值。
                if (pre != NULL && cur->val <= pre->val) {
                    return false;
                }
                pre = cur;// 更新pre为当前节点。
                cur = cur->right;// 将cur更新为当前节点的右子节点，准备遍历右子树。
            }
        }
        // 如果遍历完整棵树都没有发现违反二叉搜索树性质的情况，则返回true，表明是有效的二叉搜索树。
        return true;
    }
};

ps：以上皆是本人在探索算法旅途中的浅薄见解，诚挚地希望得到各位的宝贵意见与悉心指导，若有不足或谬误之处，还请多多指教。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1586546.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

linux中rpm包与deb包的区别及使用

linux中rpm包与deb包的区别及使用

文章目录 1. rpm与deb的区别2. deb软件包的格式和使用2.1 deb软件包命令遵行如下约定2.2 dpkg命令2.3 apt-命令 3. Unix和Linux的区别Reference 1. rpm与deb的区别 有的系统只支持使用rpm包安装&#xff0c;有的只支持deb包安装&#xff0c;混乱安装会导致系统问题。 关于rpm和…
阅读更多...
绿联 安装火狐浏览器（Firefox），支持访问路由器

绿联 安装火狐浏览器（Firefox），支持访问路由器

绿联 安装火狐浏览器&#xff08;Firefox&#xff09;&#xff0c;支持访问路由器 1、镜像 linuxserver/firefox:latest 前置条件&#xff1a;动态公网IP。 已知问题&#xff1a; 直接输入中文时&#xff0c;不能完整输入&#xff0c;也可能输入法无法切换到中文&#xff0c;可…
阅读更多...
【LeetCode刷题笔记】LeetCode 1365.有多少小于当前数字的数字

【LeetCode刷题笔记】LeetCode 1365.有多少小于当前数字的数字

创作不易&#xff0c;本篇文章如果帮助到了你&#xff0c;还请点赞 关注支持一下♡>&#x16966;<)!! 主页专栏有更多知识&#xff0c;如有疑问欢迎大家指正讨论&#xff0c;共同进步&#xff01; 更多算法知识专栏&#xff1a;算法分析&#x1f525; 给大家跳段街舞感谢…
阅读更多...
【STM32G431RBTx】备战蓝桥杯嵌入式→省赛试题→第十四届

【STM32G431RBTx】备战蓝桥杯嵌入式→省赛试题→第十四届

文章目录 前言一、题目二、模块初始化三、代码实现interrupt.h:interrupt.c:main.h:main.c: 四、完成效果五、总结 前言 无 一、题目 二、模块初始化 1.LCD这里不用配置&#xff0c;直接使用提供的资源包就行 2.KEY, 四个按键IO口都要配置&#xff0c;分别是PB0, PB1,PB2,PA…
阅读更多...
看了下雷军的两份个人简历，的确厉害。。。

看了下雷军的两份个人简历，的确厉害。。。

最近在网上浏览信息时&#xff0c;偶然看到了雷军的两份简历&#xff0c;一份是详细的工作履历&#xff0c;另一份则是他的干部履历表。 从大学时期开始&#xff0c;雷军就展现出了非凡的才华和毅力。高考成绩惊人&#xff0c;仅仅丢了2分&#xff0c;堪称完美&#xff0c;被武…
阅读更多...
Linux网络名称空间和虚拟机有何区别

Linux网络名称空间和虚拟机有何区别

在Linux系统中&#xff0c;网络名称空间和虚拟机都是实现资源隔离和虚拟化的技术&#xff0c;但它们在设计理念、实现机制、资源消耗、使用场景等方面存在着显著的区别。本文旨在全方位、系统性地分析这两种技术的区别。&#x1f50d; 1. 设计理念与实现机制 1.1. 网络名称空…
阅读更多...
Qt Creator 12.0.2 debug 无法查看变量的值 Expression too Complex

Qt Creator 12.0.2 debug 无法查看变量的值 Expression too Complex

鼠标放在局部变量上提示“expression too complex”。 在调试窗口也看不到局部变量的值。 这应该是qt的一个bug&#xff0c;https://bugreports.qt.io/browse/QTCREATORBUG-24180 暂时解决方法&#xff1a; 如下图&#xff0c;需要右键项目然后执行"Clean"和&quo…
阅读更多...
LeetCode第十六题: 掌握双指针技巧 最接近的三数之和 【python】

LeetCode第十六题: 掌握双指针技巧 最接近的三数之和 【python】

&#x1f464;作者介绍&#xff1a;10年大厂数据\经营分析经验&#xff0c;现任大厂数据部门负责人。 会一些的技术&#xff1a;数据分析、算法、SQL、大数据相关、python 欢迎加入社区&#xff1a;码上找工作http://t.csdnimg.cn/Q59WX 作者专栏每日更新&#xff1a; LeetCode…
阅读更多...
ssm038汽车养护管理系统+jsp

ssm038汽车养护管理系统+jsp

汽车养护管理系统设计与实现 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术&#xff0c;让传统数据信息的管理升级为软件存储&#xff0c;归纳&#xff0c;集中处理数据信息的管理方式。本汽车养护管理系统就是在这样的大环境下诞生&#xff0c;其可以帮助管理者在短…
阅读更多...
QT实现客户端断开连接

QT实现客户端断开连接

Widget.cpp #include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget), socket(new QTcpSocket(this)) {ui->setupUi(this);//初始化界面ui->msgEdit->setEnabled(false); //不可用ui-…
阅读更多...
PTA 应急救援站选址（floyd+打印路径）

PTA 应急救援站选址（floyd+打印路径）

大学城虎溪社区有很多居民小区&#xff0c;居民小区道路图是连通的。现要在该社区新建一个应急救援站&#xff0c;且该应急救援站要和某个小区建在一起。为了使应急救援最快速&#xff0c;经各部门商量决定&#xff1a;应急救援站建好后&#xff0c;离应急救援站最远的小区到应…
阅读更多...
【SpringBoot整合系列】SpringBoot整合FastDFS(二)

【SpringBoot整合系列】SpringBoot整合FastDFS(二)

目录 SpringBoot整合FastDFSJava客户端/依赖常用api接口解释1.uploadFile参数返回值 2.uploadSlaveFile参数返回值 3.getMetadata参数返回值 4.overwriteMetadata参数&#xff1a;返回值&#xff1a;无 5.mergeMetadata参数&#xff1a;返回值&#xff1a;无 6.queryFileInfo参…
阅读更多...
数学之光照亮AI之路：探究数学背景在人工智能学习中的优势

数学之光照亮AI之路：探究数学背景在人工智能学习中的优势

在科技日新月异的今天&#xff0c;人工智能&#xff08;AI&#xff09;已成为引领未来发展的重要力量。然而&#xff0c;对于许多初涉此领域的学习者来说&#xff0c;AI的复杂性和深度常常让他们望而却步。有趣的是&#xff0c;那些数学基础扎实的人在学习AI时&#xff0c;往往…
阅读更多...
【Docker】docker快速安装部署fastdfs的镜像详细记录

【Docker】docker快速安装部署fastdfs的镜像详细记录

部署nacos的docker镜像 第一步&#xff1a; 获取fastdfs镜像1、查看镜像列表2、创建本地映射文件夹 第二步&#xff1a;运行镜像1.使用docker镜像构建tracker服务2.使用docker镜像构建Storage服务3.Storage服务中默认安装了Nginx服务4.如果需要修改storage则配置则进到以下目录…
阅读更多...
Python 全栈体系【四阶】（二十八）

Python 全栈体系【四阶】（二十八）

第五章 深度学习 四、TensorFlow 1. Tensorflow 简介 1.1 什么是 Tensorflow TensorFlow 由谷歌人工智能团队谷歌大脑&#xff08;Google Brain&#xff09;开发和维护的开源深度学习平台&#xff0c;是目前人工智能领域主流的开发平台&#xff0c;在全世界有着广泛的用户群…
阅读更多...
【电子通识】热风枪的结构与使用方法

【电子通识】热风枪的结构与使用方法

热风枪的结构 热风枪是专门用来拆焊、焊接贴片元器件和贴片集成电路的焊接工具&#xff0c;它主要由主机和热风焊枪两大部分构成。 热风枪主要有电源开关、风速设置、温度设置、热风连接等部件组成。根据不同品牌和价位的热风枪&#xff0c;有一些功能齐全的也集成了烙铁功能。…
阅读更多...
vivado 设置 ILA 核以执行测量

vivado 设置 ILA 核以执行测量

设置 ILA 核以执行测量 您添加到自己的设计中的 ILA 核会显示在“硬件 (Hardware) ”窗口中的目标器件下。如果未显示这些 ILA 核 &#xff0c; 请右键 单击器件并选择“ Refresh Device ”。这样将重新扫描 FPGA 或 ACAP 并刷新“ Hardware ”窗口。 注释 &#xff1a…
阅读更多...
集装箱5G智能制造工厂数字孪生可视化平台，推进企业数字化转型

集装箱5G智能制造工厂数字孪生可视化平台，推进企业数字化转型

集装箱5G智能制造工厂数字孪生可视化平台&#xff0c;推进企业数字化转型。在当下数字化转型的热潮中&#xff0c;集装箱5G智能制造工厂数字孪生可视化平台成为了推动企业转型升级的重要工具。这一平台将先进的5G技术与智能制造相结合&#xff0c;通过数字孪生技术实现生产过程…
阅读更多...
Doodle Jump — 使用FlutterFlame开发游戏真不错！

Doodle Jump — 使用FlutterFlame开发游戏真不错！

前言 最近网上冲浪的时候&#xff0c;我偶然发现了一个国外的游戏网站&#xff0c;里面聚集了各种有趣的小游戏&#xff0c;类似于国内的4399。在浏览时&#xff0c;我遇到了一款经典的小游戏&#xff1a;Doodle Jump。上一次玩还是在上小学的时候&#xff0c;那时候父母在厨房…
阅读更多...
【电子通识】普通电阻、敏感电阻、可调电阻的种类和特点

【电子通识】普通电阻、敏感电阻、可调电阻的种类和特点

电阻的作用 在【分立元件】理解电阻 中我们知道电阻是在电路中对电流产生阻碍作用的元件。电阻是电子产品中最基本、最常用的电子元件之一。 有各产品的电路板中基本都有电阻器&#xff0c;通常起限流、滤波或分压等作用。实际上&#xff0c;电阻器的种类很多&#xff0c;根据其…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023