👤作者介绍：10年大厂数据\经营分析经验，现任大厂数据部门负责人。
会一些的技术：数据分析、算法、SQL、大数据相关、python欢迎加入社区：码上找工作
http://t.csdnimg.cn/Q59WX
作者专栏每日更新：
LeetCode解锁1000题: 打怪升级之旅LeetCode解锁1000题: 打怪升级之旅
python数据分析可视化：企业实战案例
备注说明：方便大家阅读，统一使用python，带必要注释，公众号 数据分析螺丝钉 一起打怪升级
题目描述
给你一个长度为 n 的整数数组 nums 和 一个目标值 target。请你从 nums 中选出三个整数，使它们的和与 target 最接近。
返回这三个数的和。
假定每组输入只存在恰好一个解。
示例 1：
输入：nums = [-1,2,1,-4], target = 1
输出：2
解释：与 target 最接近的和是 2 (-1 + 2 + 1 = 2) 。
示例 2：
输入：nums = [0,0,0], target = 1
输出：0算法比较
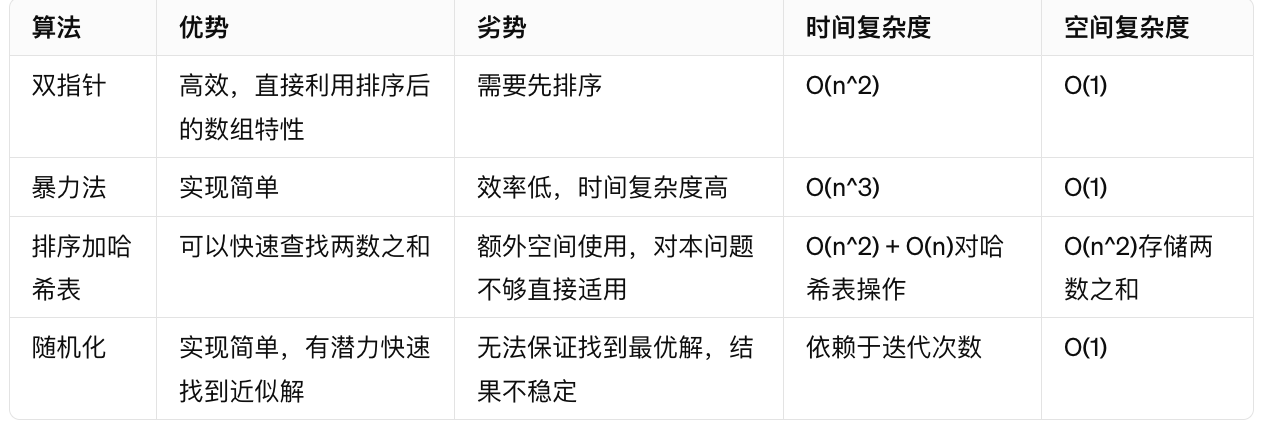
下表总结了几种解决“最接近的三数之和”问题的算法的优劣势以及它们的时间和空间复杂度
- 时间复杂度表示算法执行的速度，或者说完成算法需要的时间。时间复杂度低的算法在处理大数据集时更有优势。
- 空间复杂度表示算法在执行过程中需要的存储空间大小。空间复杂度低意味着算法对内存的占用较小。
解题思路
1. 暴力法
这是最直接的方法，即尝试数组中所有可能的三数组合，并找到和最接近目标值 target 的组合。这种方法简单易懂，但时间复杂度非常高。
- 首先定义了一个函数
threeSumClosest接收一个数组nums和一个目标值target。 - 它使用三层嵌套循环来穷举所有可能的三个数字的组合，并计算这三个数的和。如果这个和更接近目标值
target，就更新closest_sum为这个和。 - 最后，函数返回最接近
target的三数之和。
代码实现
def threeSumClosest(nums, target):
closest_sum = float('inf') # 设置一个非常大的初始值
min_diff = float('inf') # 记录与target的最小差值
# 对每个数进行遍历，计算所有可能的三数之和
for i in range(len(nums)-2):
for j in range(i+1, len(nums)-1):
for k in range(j+1, len(nums)):
sum = nums[i] + nums[j] + nums[k]
diff = abs(target - sum)
# 如果当前和更接近target，更新closest_sum
if diff < min_diff:
min_diff = diff
closest_sum = sum
return closest_sum
# 示例
nums = [-1, 2, 1, -4]
target = 1
print(threeSumClosest(nums, target))
算法分析
- 时间复杂度：O(n^3)，因为需要三层循环遍历所有可能的组合。
- 空间复杂度：O(1)，因为只需要常数级别的额外空间。
2. 双指针法
-
排序：首先，我们需要对数组进行排序。排序是使用双指针技巧的前提，因为排序后才能通过指针的移动来控制和的大小。
-
双指针遍历：遍历数组，对于每个元素
nums[i]，设置两个指针，一个指向i+1，另一个指向数组的最末尾。通过比较三数之和与target的差值，移动指针来逼近目标值。 -
更新最接近值：在移动指针的过程中，如果遇到更接近目标值
target的三数之和，就更新最接近值。
代码实现
def threeSumClosest(nums, target):
nums.sort()
closest_sum = float('inf')
for i in range(len(nums) - 2):
left, right = i + 1, len(nums) - 1
while left < right:
current_sum = nums[i] + nums[left] + nums[right]
if abs(current_sum - target) < abs(closest_sum - target):
closest_sum = current_sum
if current_sum < target:
left += 1
elif current_sum > target:
right -= 1
else:
return target # 直接返回目标值
return closest_sum
算法分析
- 时间复杂度：排序的时间复杂度是 O(n log n)，遍历数组并使用双指针的时间复杂度是 O(n^2)，因此总体时间复杂度是 O(n^2)。
- 空间复杂度：除了排序，我们只使用了常数额外空间，所以空间复杂度是 O(1)。
3. 排序加哈希表
这是一种折中的方法，将三数之和转换为两数之和的问题。对数组排序后，对于每个元素，使用哈希表快速查找是否存在满足条件的另外两个数。
解题思路
- 排序：首先对数组进行排序，这是为了后续能更高效地使用双指针技巧。
- 使用哈希表存储：考虑将每两个数的和以及这两个数的索引存储在哈希表中。这样做的目的是为了快速查找是否存在一个数，使得该数与某个和相加接近于目标值。
- 搜索和更新：遍历每个数，对于每个数，查找哈希表中是否存在与之配对的和，使得三数之和最接近于目标值，并更新最接近的和。
代码实现
def threeSumClosest(nums, target):
nums.sort() # 对数组进行排序
closest_sum = float('inf') # 初始化最接近的和为无穷大
sums_hash = {} # 初始化哈希表来存储两数之和和对应的索引
# 填充哈希表
for i in range(len(nums)):
for j in range(i+1, len(nums)):
two_sum = nums[i] + nums[j]
# 哈希表的键为两数之和，值为这两个数的索引
if two_sum not in sums_hash:
sums_hash[two_sum] = []
sums_hash[two_sum].append((i, j))
# 遍历数组，使用哈希表查找最接近的和
for k in range(len(nums)):
for sum_val, indices in sums_hash.items():
for index_pair in indices:
if k not in index_pair: # 确保不重复使用相同的元素
current_sum = sum_val + nums[k]
if abs(current_sum - target) < abs(closest_sum - target):
closest_sum = current_sum
return closest_sum
算法分析
- 时间复杂度：O(n^2)，对每个元素都可能需要一次线性时间的遍历。
- 空间复杂度：O(n) 这种方法的空间复杂度较高，因为它存储了大量的两数之和和索引对。
4. 随机化算法
可以使用随机化技术，例如蒙特卡洛方法，随机选择三个数计算其和，多次迭代以提高找到最接近解的几率。
解题思路
- 随机选择：随机选择三个数，计算它们的和，并记录这个和与目标值
target的差距。 - 迭代改进：重复上述过程多次，每次尝试时，如果找到了更接近目标值的和，就更新这个最接近的和。
- 停止条件：设定一个迭代次数作为停止条件，防止算法运行时间过长。
这种方法的优点是实现简单，能够在一定程度上探索解空间，但缺点是不能保证找到最优解，解的质量高度依赖于随机选择和迭代次数。
代码实现
import random
def threeSumClosest(nums, target):
closest_sum = float('inf') # 初始化最接近的和为无穷大
iterations = 10000 # 设定迭代次数
for _ in range(iterations):
# 随机选择三个不同的索引
indices = random.sample(range(len(nums)), 3)
# 计算这三个数的和
current_sum = sum(nums[i] for i in indices)
# 如果这个和更接近target，更新closest_sum
if abs(current_sum - target) < abs(closest_sum - target):
closest_sum = current_sum
return closest_sum
# 示例
nums = [-1, 2, 1, -4]
target = 1
print(threeSumClosest(nums, target))
算法分析
- 时间复杂度：这取决于迭代次数，可能无法保证找到最优解。
- 空间复杂度：O(1)，不需要额外空间。
综合比较
这些方法与双指针方法相比，可能在特定情况下更加高效或简单。但从时间复杂度的角度看，双指针方法通常是最优的选择，尤其是对于大数据集。暴力法在实际应用中通常不可行，因为它的时间复杂度过高；二分查找法和哈希表方法在一些情况下可以提高效率，但它们要么需要额外的预处理步骤，要么需要额外的空间开销；随机化算法可能无法保证总是得到最接近的解。
在选择解题策略时，除了考虑时间和空间复杂度之外，还应该考虑实现的复杂性、代码的可读性以及算法的稳定性。在面试或竞赛中，双指针技术是一个常用且高效的解决方案，可以作为首选方法来解决类似的问题。
