一、互斥锁

先看一个并发情况，同时操作一个全局变量，如果没有锁会怎么样

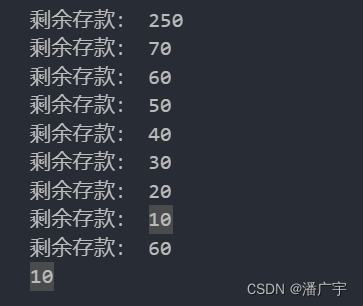
假设有1000个goroutines并发进行银行余额的扣除，每次都扣除10元，起始的总余额是10000，理论上并发执行完应该是0对不对，但实际却不是

import (
	"fmt"
	"sync"
)

var balance uint = 10000

func withdraw(amount uint) {
	balance = balance - amount
	fmt.Println("剩余存款：", balance)
	defer wg.Done()
}

func getBalance() uint {
	return balance
}

func main() {
	for i := 1; i <= 1000; i++ {
		wg.Add(1)
		go withdraw(10)
	}

	wg.Wait()
	fmt.Println(getBalance())
}

得到的结果如下：

这时候就需要引入一个锁来保护balance全局变量，在并发goroutines执行的情况下，防止其他goroutines获取到balance变量进行操作（其他goroutines会处于等待锁的状态）

import (
	"fmt"
	"sync"
)

var balance uint = 10000
var mu sync.Mutex
var wg sync.WaitGroup

func withdraw(amount uint) {
	//如果其它的goroutine已经获得了这个锁的话，这个操作会被阻塞直到其它goroutine调用了Unlock使该锁变回可用状态。mutex会保护共享变量。
	mu.Lock()                       ******************* 增加锁 **********************
	balance = balance - amount
	fmt.Println("剩余存款：", balance)
	mu.Unlock()                     ******************* 释放锁 **********************
	defer wg.Done()
}

func getBalance() uint {
	return balance
}

func main() {
	for i := 1; i <= 1000; i++ {
		wg.Add(1)
		go withdraw(10)
	}

	wg.Wait()
	fmt.Println(getBalance())
}

得到的结果如下：

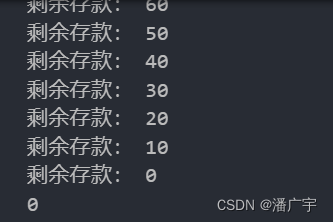
二、读写锁

RWMutex，即读写互斥锁，适用于读操作远远多于写操作的场景，当多个goroutine需要频繁地读取某个共享资源，而写入操作相对较少时，使用RWMutex可以提高并发性能。

func getBalance() uint {
	rwMu.RLock()               *********  加锁读取 ********
	defer rwMu.RUnlock()       ********* 返回释放锁 ********
	return balance
}

原理：RWMutex允许多个goroutine同时获取读锁（RLock），进行并发读操作，而写锁（Lock）则是互斥的，同一时间只允许一个goroutine进行写操作。当一个goroutine获取读锁时，其他goroutine也可以继续获取读锁来读取数据，而不需要等待。只有当有goroutine尝试获取写锁时，读锁才会被阻塞，这样可以有效地提高并发读取的效率。

sync.RWMutex锁的设计就是为了优化读操作频繁的场景。它能够区分读锁（RLock）和写锁（Lock）

读锁（RLock）：
当一个goroutine需要读取共享资源时，它会尝试获取读锁。如果当前没有其他goroutine持有写锁，那么它可以成功获取读锁，并且可以并发地读取数据。如果有其他goroutine已经持有读锁，新的读锁请求也会被允许，从而允许多个goroutine同时读取。

写锁（Lock）：
当一个goroutine需要写入共享资源时，它会尝试获取写锁。在写锁被获取之前，所有的读锁和写锁请求都会被阻塞。这意味着，一旦有goroutine开始写操作，其他想要读取或写入的goroutine都必须等待，直到写操作完成并且写锁被释放。

锁的释放：
当一个goroutine完成读取或写入操作后，它会释放相应的锁。如果是读操作完成，它会释放读锁，这样其他正在等待的goroutine就可以获取读锁并开始读取。如果是写操作完成，它会释放写锁，这样其他正在等待的读锁或写锁请求就可以继续进行。

RWMutex的这种设计使得在读操作远多于写操作的情况下，可以提高程序的并发性能。因为多个goroutine可以同时读取，而不需要等待写操作完成，这样就减少了锁竞争，提高了整体的吞吐量。然而，需要注意的是，RWMutex并不是在所有情况下都能提高性能。如果写操作非常频繁，或者读写操作几乎同等频繁，使用RWMutex可能会导致性能下降，因为写操作会阻塞所有读锁和写锁的请求。在这种情况下，使用Mutex可能会更加合适。