算法训练营第24天回溯（组合）

news2024/11/30 4:39:18

回溯（组合）

模板

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

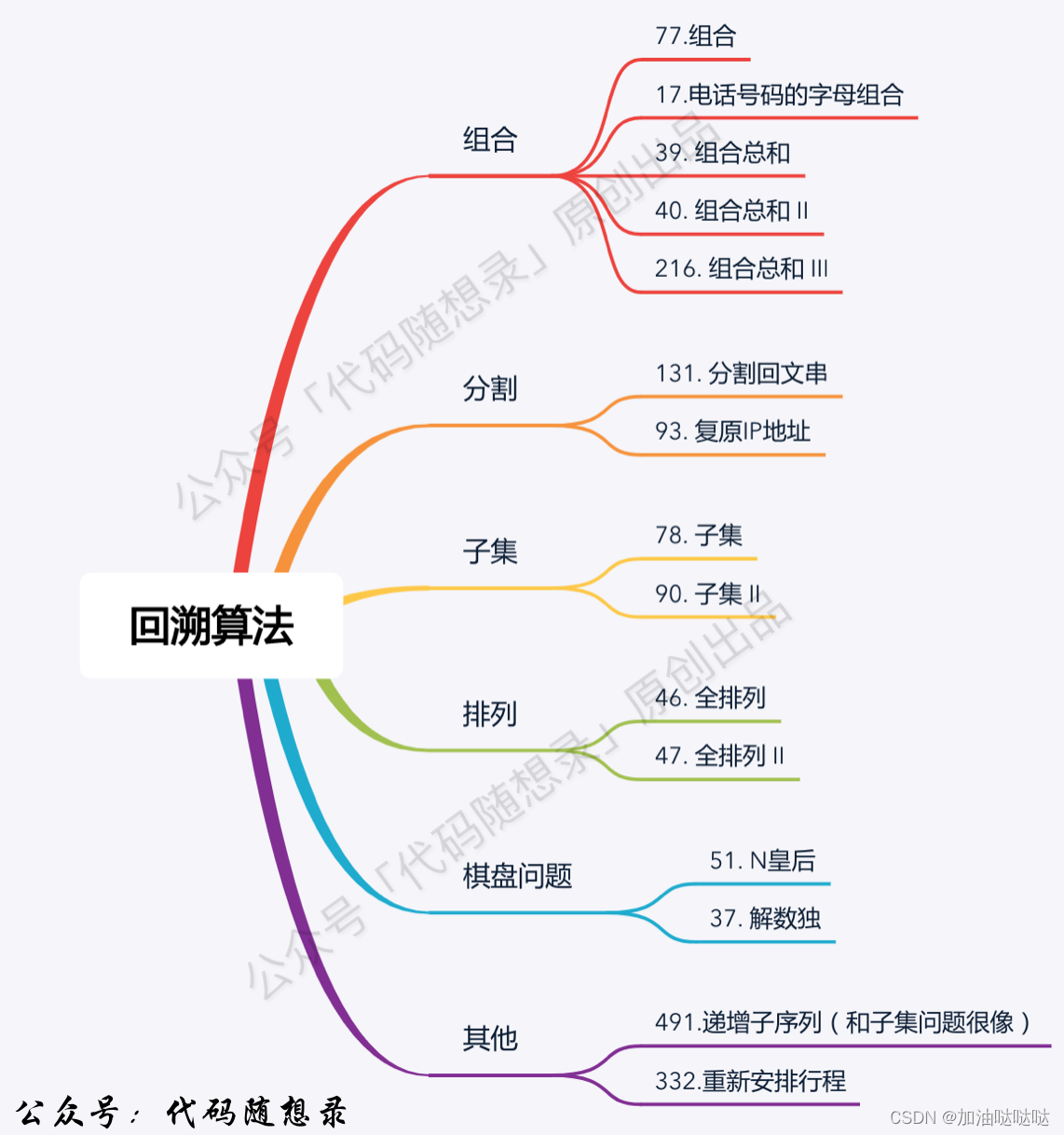
在这里插入图片描述

在这里插入图片描述

第77题. 组合

力扣题目链接(opens new window)

题目

给定两个整数 n 和 k，返回 1 … n 中所有可能的 k 个数的组合。

示例: 输入: n = 4, k = 2 输出: [ [2,4], [3,4], [2,3], [1,2], [1,3], [1,4],]

解答

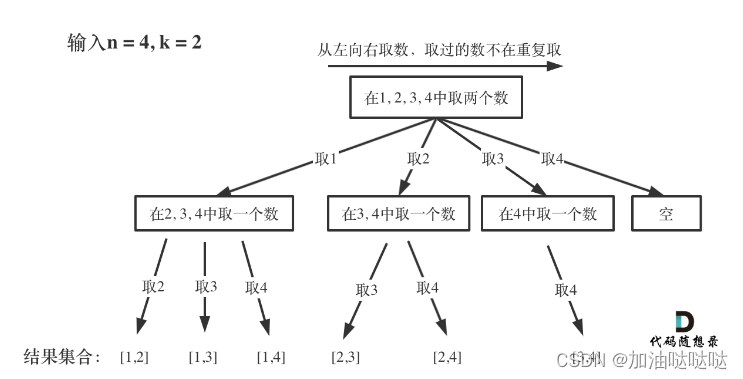
正常方法（不够快，遍历了许多没必要的枝）

一个递归就相当于嵌套了一个for（每个递归都是一个分而治之的过程，第一个for是为了取第一个数，之后每次递归都再取一个）

在这里插入图片描述

class Solution {
	List<List<Integer>> results = new ArrayList<>();
	List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
		backtracking(n,k,1);
		return results;
    }

	void backtracking(int n, int k,int index){
		if (path.size() == k){
			results.add(new ArrayList<>(path));
			return;
		}

		for (int i = index; i <= n; i++) {//每个for都是一个单独的横向分支
			path.add(i);
			backtracking(n,k,i + 1);//每个递归都是纵向枝
			path.remove(path.size() - 1);
		}
	}
}
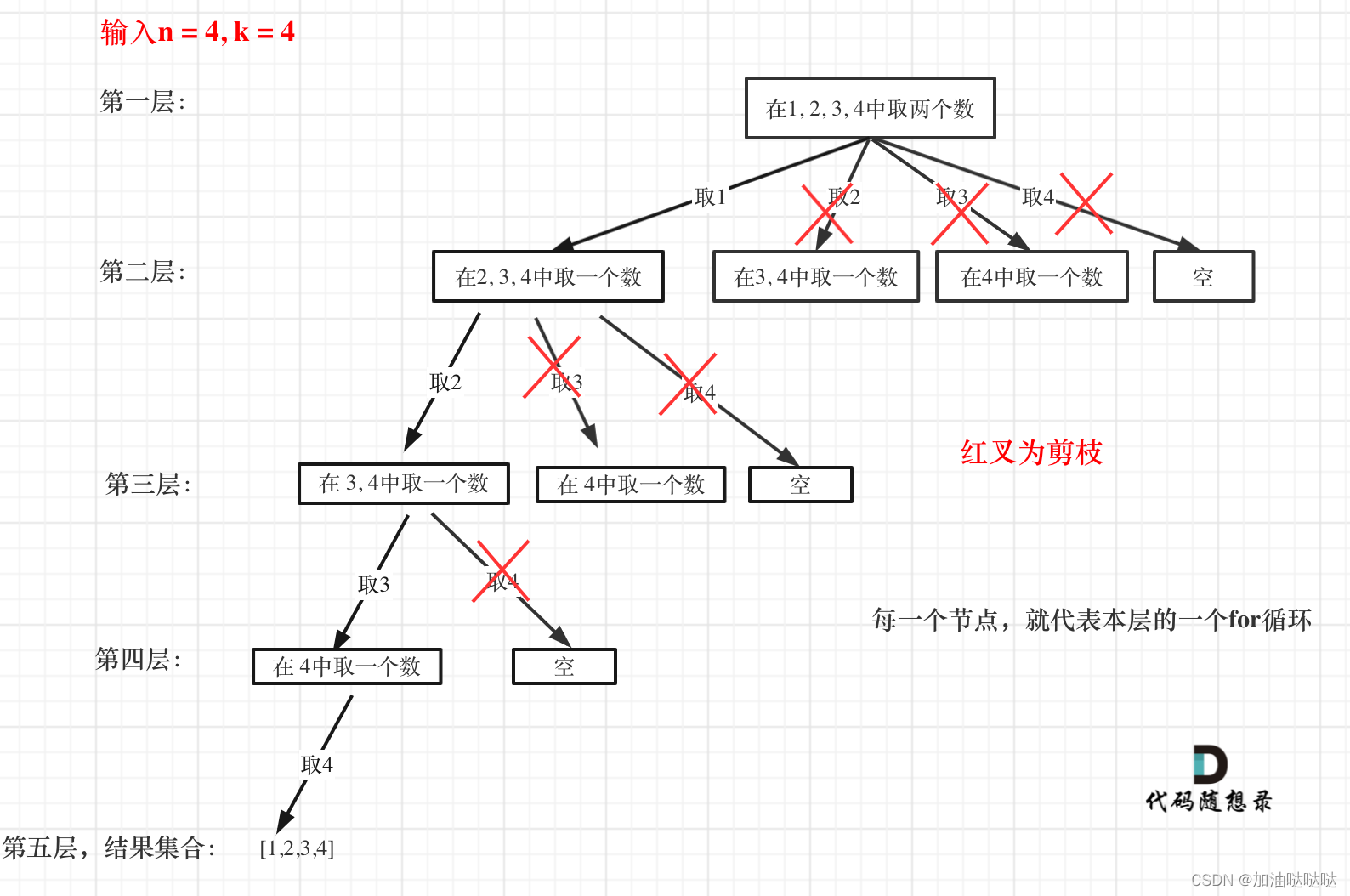
剪枝优化

只是修改了for的终止条件，去除没用的枝

在这里插入图片描述

  1. 已经选择的元素个数：path.size();
  2. 所需需要的元素个数为: k - path.size();
  3. 列表中剩余元素（n-i） >= 所需需要的元素个数（k - path.size()）
  4. 在集合n中至多要从该起始位置 : i <= n - (k - path.size()) + 1，开始遍历
    • 例：如果n = 4， k = 4， 那么只有index = 1这条枝需要保留，i<= 1， 因为此时path为空，所以k - path = 4，故n - (k - path.size()) + 1
class Solution {
	List<List<Integer>> results = new ArrayList<>();
	List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combine(int n, int k) {
		backtracking(n,k,1);
		return results;
    }

	void backtracking(int n, int k,int index){
		if (path.size() == k){
			results.add(new ArrayList<>(path));
			return;
		}

		for (int i = index; i <= n - (k - path.size()) + 1; i++) {//如果n = 4， k = 4， 那么只有index = 1这条枝需要保留，i<= 1， 因为此时path为空，所以k - path = 4，故n - (k - path.size()) + 1
			path.add(i);
			backtracking(n,k,i + 1);
			path.remove(path.size() - 1);
		}
	}
}

216.组合总和III

力扣题目链接(opens new window)

题目

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

  • 所有数字都是正整数。
  • 解集不能包含重复的组合。

示例 1: 输入: k = 3, n = 7 输出: [[1,2,4]]

示例 2: 输入: k = 3, n = 9 输出: [[1,2,6], [1,3,5], [2,3,4]]

解答

涉及到了两处剪枝

  1. 如果目前相加的和已经大于sum，并且没有达到k个元素，也就意味着后面再加只会更大，剪枝就行了

    if (path.size() == k || sum >= n){//sum >= n是为了求和时的剪枝
    if (sum == n && path.size() == k)
        results.add(new ArrayList<>(path));
    return;
}
//等价于
if (sum > n) return;//对sum剪枝

if (sum == n && path.size() == k){
    results.add(new ArrayList<>(path));
    return;
}

  2. 对个数进行剪枝，与上一个题一样

    for (int i = index; i <= 9 - (k - path.size()) + 1; i++) 
//等价于
if (path.size() > k ) return;//对数量剪枝

class Solution {
	List<List<Integer>> results = new ArrayList<>();
	List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
		backtracking(k,n,1,0);
		return results;
    }

	void backtracking(int k,int n,int index,int sum){
		if (path.size() == k || sum >= n){//sum >= n是为了求和时的剪枝
			if (sum == n && path.size() == k)
				results.add(new ArrayList<>(path));
			return;
		}

		for (int i = index; i <= 9 - (k - path.size()) + 1; i++) {//9 - (k - path.size()) + 1是为了数量不够时的剪枝
			path.add(i);
			backtracking(k,n,i + 1,sum + i);
			path.remove(path.size() - 1);
		}
	}
}

等价形式

class Solution {
	List<List<Integer>> results = new ArrayList<>();
	List<Integer> path = new ArrayList<>();
    public List<List<Integer>> combinationSum3(int k, int n) {
		backtracking(k,n,1,0);
		return results;
    }

	void backtracking(int k,int n,int index,int sum){

		if (path.size() > k ) return;//对数量剪枝

		if (sum > n) return;//对sum剪枝

		if (sum == n && path.size() == k){
			results.add(new ArrayList<>(path));
			return;
		}

		for (int i = index; i <= 9; i++) {
			path.add(i);
			backtracking(k,n,i + 1,sum + i);
			path.remove(path.size() - 1);
		}
	}
}

17.电话号码的字母组合

力扣题目链接(opens new window)

题目

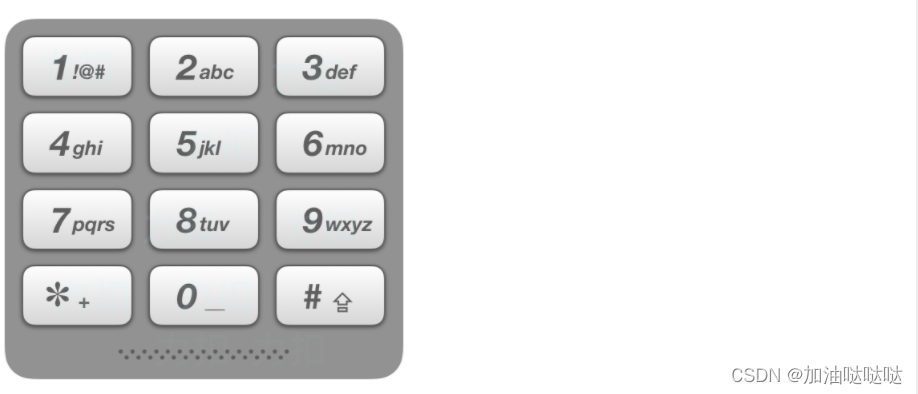
给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

在这里插入图片描述

示例:

  • 输入：“23”
  • 输出：[“ad”, “ae”, “af”, “bd”, “be”, “bf”, “cd”, “ce”, “cf”].

说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

解答

有几个字母深度就是几

注意回溯后的组合一定是无序的，因为会先把最后一个全部找完，再找前一个（不涉及顺序，才能这么回溯）

例：

测试用例：“234”

结果：[adg, adh, adi, aeg, aeh, aei, afg, afh, afi, bdg, bdh, bdi, beg, beh, bei, bfg, bfh, bfi, cdg, cdh, cdi, ceg, ceh, cei, cfg, cfh, cfi]

  1. adg：2的第一个，3的第一个，4的第一个，此时index + 1= 3，达到结束条件，将adg加入
  2. 将最后一个g弹出，进入index = 3的for循环，再次将4对应的第二个h放入path，然后将adh加入
  3. 同理，将adi加入
  4. 此时第三个for已经结束，跳出该循环，第三个递归结束，此时index = 2，并且当前的path中只有ad，然后执行回溯，d再次被弹出
  5. 进入第二个for的第二层，即将3对应的第二个元素e加入，进入递归，此时index没达到4，所以继续进入下一层递归，将4的第一个元素g再加入，即得到aeg
  6. 依次类推
class Solution {
	List<String> result = new ArrayList<>();
	StringBuffer path = new StringBuffer();
    public List<String> letterCombinations(String digits) {
		if (Objects.equals(digits, "") || Objects.equals(digits, " "))
			return result;
		Map<Character,String> map = new HashMap<>();
		map.put('2', "abc");
		map.put('3', "def");
		map.put('4', "ghi");
		map.put('5', "jkl");
		map.put('6', "mno");
		map.put('7', "pqrs");
		map.put('8', "tuv");
		map.put('9', "wxyz");
		backtracking(digits,map,0);
		return result;
    }
	void backtracking(String digits,Map<Character,String> map,int index){
		if (index == digits.length()){
			result.add(path.toString());
			return;
		}

		String element = map.get(digits.charAt(index));
		for (int i = 0; i < element.length(); i++) {
			path.append(element.charAt(i));
			backtracking(digits,map,index + 1);
			path.deleteCharAt(path.length() - 1);//一定是无序的
		}
	}
}

39. 组合总和

力扣题目链接(opens new window)

题目

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

  • 所有数字（包括 target）都是正整数。
  • 解集不能包含重复的组合。

示例 1：

  • 输入：candidates = [2,3,6,7], target = 7,
  • 所求解集为： [ [7], [2,2,3] ]

示例 2：

  • 输入：candidates = [2,3,5], target = 8,
  • 所求解集为： [ [2,2,2,2], [2,3,3], [3,5] ]

解答

巨大误区：

必须要有startIndex参数，只是startIndex的传入参数根据情况不同而不同，但是必须要有，如果没有就会出现重复的元素，也就是可能出现在这里插入图片描述
这种情况，因为如果使用下面的代码，

		for (int i = 0; i < candidates.length; i++) {
			path.add(candidates[i]);
			backtracking(candidates, target, sum + candidates[i], i);
			path.removeLast();//sum在当前这一轮中没有变，也就是相当于已经进行了回溯
		}

也就相当于每次都是从0开始，也就意味着当当前递归函数结束，返回上一层时，上一层重新进入下一层的递归树时，还是会遍历之前已经遍历过的元素，导致重复组合的产生

例：[2,3,6,7] 7

  1. 2 2 2 2 remove
  2. 2 2 2 3 remove
  3. 2 2 2 6 remove
  4. 2 2 2 7 remove
  5. 2 2 3 return
  6. 2 2 6 remove
  7. 2 2 7 remove
  8. 2 3 2出现了重复，因为在当这一轮来说，下一层递归不应该在遍历当前遍历的元素之前的元素，因为在之前已经遍历过了，所以就会出现重复的组合

正确代码应该是

		for (int i = startIndex; i < candidates.length; i++) {
			path.add(candidates[i]);
			backtracking(candidates, target, sum + candidates[i], i);
			path.removeLast();//sum在当前这一轮中没有变，也就是相当于已经进行了回溯
		}

还应该注意必须要排序，因为如果不排序那么使用if (sum > target) return;来剪枝就是错误的

正确代码
class Solution {
	List<List<Integer>> result = new ArrayList<>();
	LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
		Arrays.sort(candidates);
		backtracking(candidates,target,0,0);
		return result;
    }

	void backtracking(int[] candidates,int target,int sum,int startIndex){
		if (sum > target) return;//剪枝

		if (sum == target){
			result.add(new LinkedList<>(path));
			return;
		}
		for (int i = startIndex; i < candidates.length; i++) {
			path.add(candidates[i]);
			backtracking(candidates, target, sum + candidates[i], i);
			path.removeLast();//sum在当前这一轮中没有变，也就是相当于已经进行了回溯
		}
	}
}
总结
  1. 一定要是有index，不要想当然的使用for，导致重复元素的产生
  2. 一定要排序，否则剪枝会有问题

40.组合总和II

力扣题目链接(opens new window)

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明： 所有数字（包括目标数）都是正整数。解集不能包含重复的组合。

  • 示例 1:
  • 输入: candidates = [10,1,2,7,6,1,5], target = 8,
  • 所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]
  • 示例 2:
  • 输入: candidates = [2,5,2,1,2], target = 5,
  • 所求解集为:
[
  [1,2,2],
  [5]
]

解答

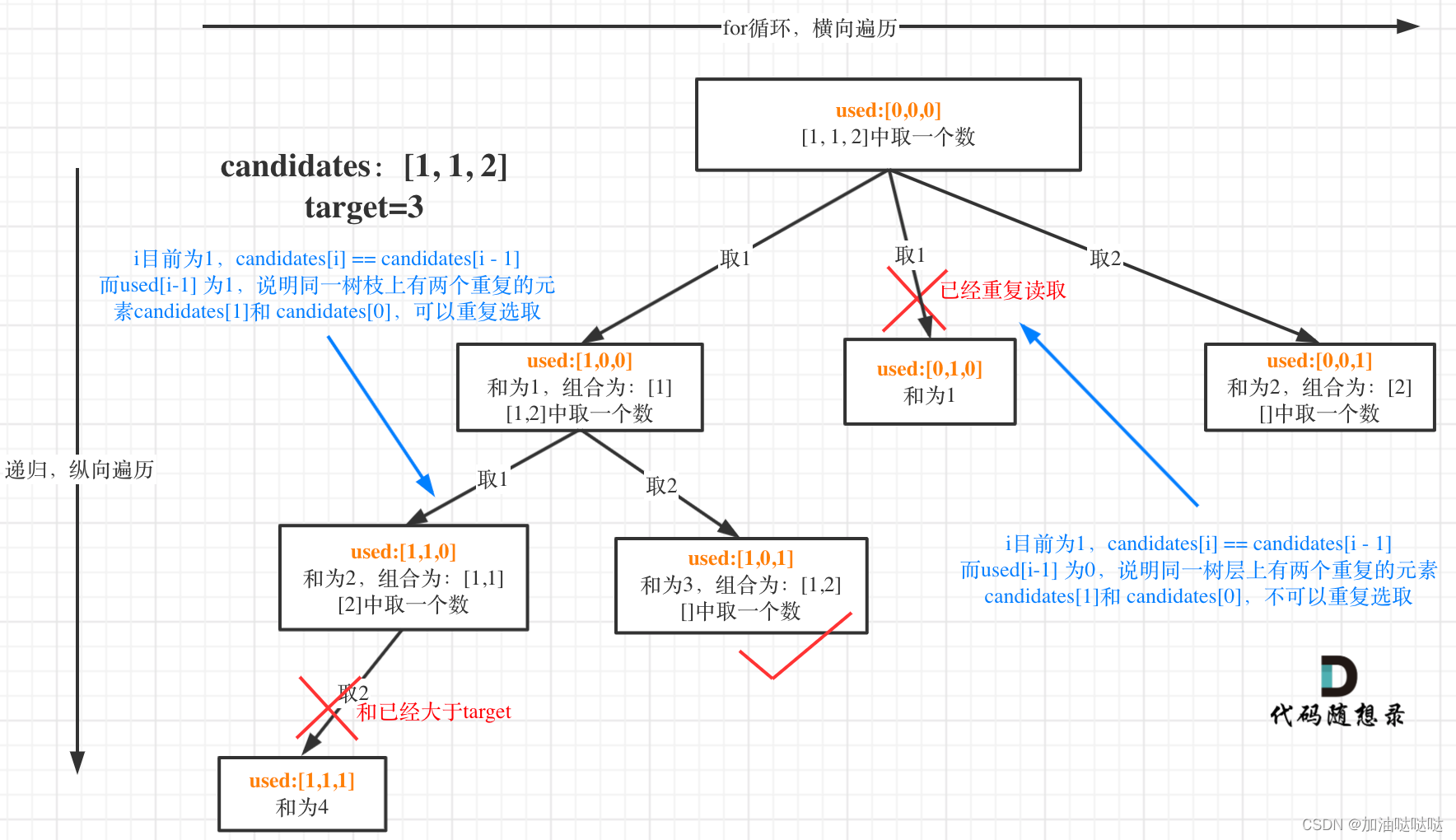
在这里插入图片描述

树枝去重

backtracking(candidates,target,sum + candidates[i],i + 1);使用i+1来防止树枝遍历相同的元素，也就是防止出现重复元素（由于每个元素只能出现一次，所以为i+1，否则就像上一个题一样为i）

树层去重

if (i > startIndex && candidates[i] == candidates[i - 1]) continue;对于同一层的元素，如果两个元素相同，就直接跳过该轮，否则也会出现重复元素

class Solution {
	List<List<Integer>> result = new ArrayList<>();
	LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
		Arrays.sort(candidates);
		backtracking(candidates,target,0,0);
		return result;
    }
	void backtracking(int[] candidates, int target , int sum, int startIndex){
		if (sum > target) return;

		if (sum == target){
			result.add(new ArrayList<>(path));
			return;
		}

		for (int i = startIndex; i < candidates.length; i++) {
			if (i > startIndex && candidates[i] == candidates[i - 1])
				continue;//因为已经排序过，所以要保证同一层的元素不相同，如果相同直接跳过
			//也就是对于path中索引相同位置的元素不能两次一致，这样可能会出现重复的组合
			path.add(candidates[i]);
			backtracking(candidates,target,sum + candidates[i],i + 1);
			path.removeLast();
		}
	}
}

求和总结

  1. 对于不包含重复元素的集合，要想防止出现元素重复的组合，即[2 , 3] [3 , 2]为重复元素的组合，就要使用startIndex来限定 backtracking(candidates,target,sum + candidates[i],i + 1);

    1. 如果是允许同一个元素在组合中多次出现，则使用 backtracking(candidates,target,sum + candidates[i],i + 1);

  2. 对于包含重复元素的集合，除了要是有startIndex外，还需要对树层元素进行判断，否则如果是[1 ,1,2,3]，target = 3，就会出现两个相同的[1,2]，因为对于第一层会遍历两次，使用if (i > startIndex && candidates[i] == candidates[i - 1]) continue;解决

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1586379.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

6.11物联网RK3399项目开发实录-驱动开发之定时器的使用（wulianjishu666）

6.11物联网RK3399项目开发实录-驱动开发之定时器的使用（wulianjishu666）

嵌入式实战开发例程【珍贵收藏&#xff0c;开发必备】&#xff1a; 链接&#xff1a;https://pan.baidu.com/s/1tkDBNH9R3iAaHOG1Zj9q1Q?pwdt41u 定时器使用 前言 RK3399有 12 个 Timers (timer0-timer11)&#xff0c;有 12 个 Secure Timers(stimer0~stimer11) 和 2 个 …
阅读更多...
LC 501.二叉搜索树中的众数

LC 501.二叉搜索树中的众数

501.二叉搜索树中的众数 给你一个含重复值的二叉搜索树&#xff08;BST&#xff09;的根节点 root &#xff0c;找出并返回 BST 中的所有 众数&#xff08;即&#xff0c;出现频率最高的元素&#xff09;。 如果树中有不止一个众数&#xff0c;可以按 任意顺序 返回。 假定 …
阅读更多...
深入浅出 -- 系统架构之在Java体系中的微服务标准组件

深入浅出 -- 系统架构之在Java体系中的微服务标准组件

前面我们介绍了微服务架构的各个组件以及各组件的职责&#xff0c;在Java领域中&#xff0c;Spring可以说是无人不知无人不晓的&#xff0c;我们现代的企业级应用和互联网应用&#xff0c;很大一部分都是构建在Spring生态体系上的&#xff0c;同样&#xff0c;实现微服务架构的…
阅读更多...
MySQL高级详解

MySQL高级详解

文章目录 约束概述分类主键约束概述特点定义及删除主键自增 唯一约束作用语法 非空约束作用语法 面试题&#xff1a;非空唯一约束与主键约束有什么区别默认值约束作用语法 总结 表关系及外键约束表关系概述分类一对多关系表设计外键字段设计原则 多对多关系表设定设计原则 一对…
阅读更多...
【图论】Dijkstra单源最短路径-朴素方法-简单模板（迪杰斯特拉算法）

【图论】Dijkstra单源最短路径-朴素方法-简单模板（迪杰斯特拉算法）

Dijkstra单源最短路径 问题描述 输入n 表示n个结点&#xff0c;m表示m条边&#xff0c;求编号1的结点到每个点的最短路径 输出从第一个点到第n个点的最短路径 思路 将图g[][]中所有的权值初始化为0x3f表示正无穷 将dist[]中所有的值初始化为0x3f表示从第一个点到所有点的距离…
阅读更多...
一辆新能源汽车需要多少颗传感器？

一辆新能源汽车需要多少颗传感器？

随着科技的发展和环保意识的日益提高&#xff0c;新能源汽车&#xff08;包括纯电动汽车、混合动力汽车等&#xff09;在全球范围内越来越受到欢迎。这些汽车不仅减少了碳排放&#xff0c;还推动了汽车产业的创新。然而&#xff0c;这些高科技汽车的背后&#xff0c;隐藏着许多…
阅读更多...
Qt中播放GIF动画

Qt中播放GIF动画

在Qt应用程序中&#xff0c;如果你想在QLabel控件上播放GIF动画&#xff0c;可以使用QMovie类与QLabel配合来实现。以下是详细步骤和代码示例&#xff1a; 步骤1&#xff1a;引入必要的头文件 首先&#xff0c;在你的源代码文件中包含QMovie和QLabel相关的头文件&#xff1a;…
阅读更多...
Java官网下载JDK21版本详细教程（下载、安装、环境变量配置）

Java官网下载JDK21版本详细教程（下载、安装、环境变量配置）

文章目录 前言&#xff1a;一、下载(一).链接&#xff08;直达JDK21&#xff09;(二).官网搜索&#xff08;可选其他版本&#xff09; 二、安装三、环境变量配置四、验证安装和配置五、常见问题解答 前言&#xff1a; 本文将为您提供关于Java官网下载JDK21版本的详细教程。作为…
阅读更多...
springboot在使用 Servlet API中提供的javax.servlet.Filter 过滤器 对请求参数 和 响应参数 进行获取并记录日志方案

springboot在使用 Servlet API中提供的javax.servlet.Filter 过滤器 对请求参数 和 响应参数 进行获取并记录日志方案

不多说 直接上代码 第一步 package com.xxx.init.webFilter;import com.alibaba.fastjson.JSONObject; import com.xxx.api.constant.CommonConstant; import com.xxx.api.entities.log.OperationLog; import com.xxx.init.utils.JwtHelper; import com.xxx.init.utils.Reques…
阅读更多...
King‘s AUTO的QI妙能力|实验室“总导演”

King‘s AUTO的QI妙能力|实验室“总导演”

在2023年夏天&#xff0c;两场国际赛事分别在成都、杭州盛大举办——第31届世界大学生夏季运动会&#xff08;大运会&#xff09;以及第19届亚洲运动会&#xff08;亚运会&#xff09;。为确保开幕式的顺利进行&#xff0c;大运会共进行了三次全要素彩排&#xff0c;而亚运会则…
阅读更多...
上海人工智能实验室的书生·浦语大模型学习笔记（第二期第三课——上篇）

上海人工智能实验室的书生·浦语大模型学习笔记（第二期第三课——上篇）

书生浦语是上海人工智能实验室和商汤科技联合研发的一款大模型&#xff0c;这次有机会参与试用&#xff0c;特记录每次学习情况。 一、课程笔记 本次学习的是RAG&#xff08;Retrieval Augmented Generation&#xff09;技术&#xff0c;它是通过检索与用户输入相关的信息片段…
阅读更多...
【MATLAB源码-第185期】基于matlab的16QAM系统相位偏移估计EOS算法仿真，对比补偿前后的星座图误码率。

【MATLAB源码-第185期】基于matlab的16QAM系统相位偏移估计EOS算法仿真，对比补偿前后的星座图误码率。

操作环境&#xff1a; MATLAB 2022a 1、算法描述 1. 引言 M-QAM调制技术的重要性 现代通信系统追求的是更高的数据传输速率和更有效的频谱利用率。M-QAM调制技术&#xff0c;作为一种高效的调制方案&#xff0c;能够通过在相同的带宽条件下传输更多的数据位来满足这一需求…
阅读更多...
springboot如何切换内置web服务器？

springboot如何切换内置web服务器？

切换内置web服务器 这是没有引入web依赖的服务 这是引入web依赖的服务 由此可知默认是tomcat服务器 那么如何切换内置服务器 只要有对应服务器的坐标即可自动切换&#xff0c;先排除tomcat再引入依赖&#xff0c;比如切换成jetty服务器 <dependency><groupId>org…
阅读更多...
d3dx9_43.dll丢失的一些可行的解决方案，有效解决d3dx9_43.dll丢失

d3dx9_43.dll丢失的一些可行的解决方案，有效解决d3dx9_43.dll丢失

在电脑中&#xff0c;d3dx9_43.dll文件丢失是一个相当普遍的问题。实际上&#xff0c;要解决这个问题有多种方法。今天&#xff0c;我们将讨论一下关于d3dx9_43.dll文件丢失的问题&#xff0c;并向大家介绍一些可行的解决方案。 一.快速了解d3dx9_43.dll文件 首先&#xff0c;…
阅读更多...
Linux的学习之路：6、Linux编译器-gcc/g++使用

Linux的学习之路：6、Linux编译器-gcc/g++使用

摘要 本文主要是说一些gcc的使用&#xff0c;g和gcc使用一样就没有特殊讲述。 目录 摘要 一、背景知识 二、gcc如何完成 1、预处理(进行宏替换) 2、编译&#xff08;生成汇编&#xff09; 3、汇编&#xff08;生成机器可识别代码 4、链接&#xff08;生成可执行文件或…
阅读更多...
2024-基于人工智能的药物设计方法研究-AIDD

2024-基于人工智能的药物设计方法研究-AIDD

AIDD docx 基于人工智能的药物设计方法研究 AI作为一种强大的数据挖掘和分析技术已经涉及新药研发的各个阶段&#xff0c;有望推动创新药物先导分子的筛选、设计和发现&#xff0c;但基于AI的数据驱动式创新药物设计和筛选方法仍存在若干亟待解决的问题。我们课题组的核心研究…
阅读更多...
【Entity Framework】如何使用EF中的生成值

【Entity Framework】如何使用EF中的生成值

【Entity Framework】如何使用EF中的生成值 文章目录 【Entity Framework】如何使用EF中的生成值一、概述二、默认值三、计算列四、设置主键五、显示配置值生成六、设置日期/时间值生成6.1 创建时间戳6.2 更新时间戳 七、替代值生成八、无值生成九、总结 一、概述 数据库列的值…
阅读更多...
服务器端口被扫会出现哪些风险

服务器端口被扫会出现哪些风险

一、安全风险增加端口扫描是黑客攻击的常见手段之一。通过对服务器端口进行扫描&#xff0c;黑客可以了解服务器的开放端口、服务类型以及可能存在的漏洞。一旦黑客发现漏洞并成功利用&#xff0c;就可能导致服务器被入侵&#xff0c;进而窃取数据、植入恶意软件或进行其他非法…
阅读更多...
基于SSM的电影网站（有报告）。Javaee项目。ssm项目。

基于SSM的电影网站（有报告）。Javaee项目。ssm项目。

演示视频&#xff1a; 基于SSM的电影网站&#xff08;有报告&#xff09;。Javaee项目。ssm项目。 项目介绍&#xff1a; 采用M&#xff08;model&#xff09;V&#xff08;view&#xff09;C&#xff08;controller&#xff09;三层体系结构&#xff0c;通过Spring SpringMv…
阅读更多...
编程规范（保姆级教程）

编程规范（保姆级教程）

文章目录 为什么需要编程规范&#xff1f;&#x1f4a1;代码检测工具 ESLint&#x1f4a1;代码格式化 Prettier&#x1f4a1;ESLint 与 Prettier 配合解决代码格式问题eslint支持ts约定式提交规范Commitizen助你规范化提交代码什么是 Git Hooks使用 husky commitlint 检查提交…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023