目录
1.字符串排序
2.门牌制作
3.即约分数
4.蛇型填数
5.跑步锻炼
6.七段码
7.成绩统计
8.回文日期
9.字串分值和
10.平面切分
1.字符串排序

题目解析:这个题目真没搞懂。有会的大佬教我一下谢谢。
2.门牌制作

题目解析:出过超级多这类题目,就是每位检查有2.那么统计这个门牌号有几个2数字判断完全部加和即可.
#include <iostream>
using namespace std;
int add(int x)
{
int sum = 0;
while(x)
{
int t = x % 10;
if(t == 2)
sum++;
x /= 10;
}
return sum;
}
int main()
{
int Sum = 0;
for(int i = 1; i <= 2020; i++)
{
Sum += add(i);
}
cout << Sum << endl;
return 0;
}3.即约分数

题目解析:就是求公约数==1;
#include <iostream>
using namespace std;
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
int main()
{
int ans = 0;
for(int i = 1; i <= 2020; i++)
{
for(int j = 1; j <= 2020; j++)
{
if(gcd(i, j) == 1)
{
ans++;
}
}
}
cout << ans << endl;
return 0;
}4.蛇型填数

题目解析:就是找规律,
第一行第一列:1
第二行第二列:1+1*4 = 5;
第三行第三列:1 + 1*4 + 2 * 4= 13;
...
所以第二十行第二十列:
1+1*4 + 2*4 + 3 *4 + ...+ 19*4;
#include <iostream>
using namespace std;
int main()
{
int n = 20;
int sum = 1;
for(int i = 0; i < 20; i++)
{
sum += i * 4;
}
cout << sum << endl;
return 0;
}5.跑步锻炼

题目解析:日期类问题。注意一下逻辑关系,首先要先加和再判断是否是再2020/10/1日期之内.要不然会少加.
#include <iostream>
using namespace std;
int main()
{
int year = 2000, month = 1, day = 1, weekday = 6;
int sum = 0;
int getmonthday[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
while(1)
{
if(weekday == 1 || day == 1)
{
sum += 2;
}
else if(weekday == 1 && day == 1)
{
sum += 2;
}
else
{
sum += 1;
}
if(year == 2020 && month == 10 && day == 1)//先最后一次也要加上,再判断.
break;
day++;
weekday = (weekday + 1) % 7;
if(month == 2 && ((year % 4 == 0 && year % 100 != 0) || (year % 400 == 0)))
{
if(day > getmonthday[month] + 1)
{
day = 1;
month++;
}
}
else
{
if(day > getmonthday[month])
{
day = 1;
month++;
}
}
if(month == 13)
{
month = 1;
year++;
}
}
cout << sum << endl;
return 0;
}6.七段码

题目解析:将相邻的边全部放到矩阵当中,采用dfs深搜,如果矩阵为1就是代表可以选择,算出最后这些可以选择的矩阵元素有多少种方案数.将每种每一层进行遍历,方法进行记录并且加和。由于矩阵的每个元素都使用过两次那么总次数是要/2.
#include <iostream>
using namespace std;
int graph[7][7] =
{//转化成矩阵
{1,1,0,0,0,1,0},
{1,1,1,0,0,0,1},
{0,1,1,1,0,0,1},
{0,0,1,1,1,0,0},
{0,0,0,1,1,1,1},
{1,0,0,0,1,1,1},
{0,1,1,0,1,1,1}
};
int f[7] = { 0 };
int dfs(int n, int i)
{
int sum = 1;
for (int k = 0; k < n; k++)
{
if (graph[i][k] == 1 && f[k] == 0)
{
f[k] = 1;
sum +=dfs(7, k);
f[k] = 0;//回溯
}
}
return sum;
}
int main()
{
cout << dfs(7, 0) / 2;
return 0;
}7.成绩统计
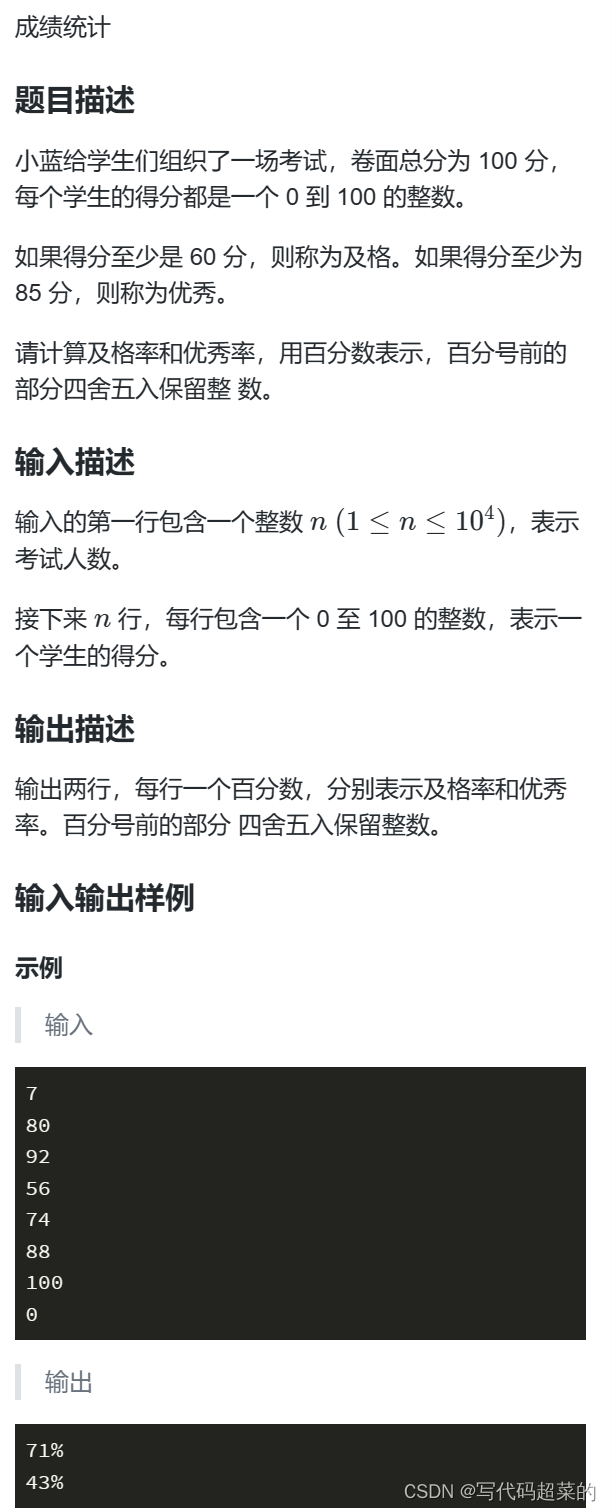
题目解析:简单统计
#include <iostream>
using namespace std;
int main()
{
double a = 0;
double b = 0;
double c;
cin >> c;
int n;
for (int i = 0; i < c; i++)
{
cin >> n;
if (n >= 60)
{
a++;
}
if (n >= 85)
{
b++;
}
}
int x =(a * 100.0)/c+0.5;
int y =(b * 100.0)/c+0.5;
cout << x << "%" << endl << y << "%";
return 0;
}8.回文日期

题目解析:可以先找到年份在输入年份之间,再对于年份逆置变成月份和日份,并且符合真正日历时间就是一种答案。
#include<iostream>
using namespace std;
int daymonth[13] = {0, 31, 28, 31, 30, 31, 30, 31, 31, 30, 31, 30, 31};
bool check(int date)
{
int year = date / 10000;
int month = (date / 100) % 100;
int day = date % 100;
if(month < 0 || month > 12) return false;
if(day ==0 || month != 2 && day > daymonth[month]) return false;
if(month == 2 )
{
int leap = year % 100 && year % 4 == 0 || year % 400 == 0;
if(day > daymonth[month] + leap) return false;
}
}
int main()
{
int date1, date2;
cin >> date1 >> date2;
int ans = 0;
for(int i = 1000; i <= 10000; i++)
{
//年份范围
int date = i, x = i;
for(int j = 0; j < 4; j ++ )
date = date * 10 + x % 10, x /= 10;
if(date1 <= date && date <= date2 && check(date))
{
ans++;
}
}
cout << ans << endl;
return 0;
}9.字串分值和

题目解析: 题目意思可以用一个例子来表示:
f[a] = 1;
f[ab] = 2;
f[aba] = 1;
那么就是相同的字符就会影响贡献点。
就拿ababc举例子;下面写出子串;
可以分析出来出现第二次的总和是等于第二次出现次数减去第一次出现的次数.再将全部的加和.那么如何求出每次出现的和;可以分为首次出现和多次出现.
首次出现: sum += (下标+1) * (字符长度 - 下标);
多次出现: sum += 本次出现-上一次出现的个数. 将上次出现的存放到一个数组中
= (下标 + 1 - 上次数组) * (字符长度 - 下标).
#include <iostream>
#include<string>
using namespace std;
long long num[26] = {0};
int main()
{
string s;
cin >> s;
long long len = s.size();
long long sum = 0;
for(long long i = 0; i < len; i++)
{
if(num[s[i] - 'a'] == 0)//没有被使用过
{
sum += (i + 1) * (len - i);
num[s[i] - 'a'] = i + 1;
}
else//使用过
{
sum += (i + 1 - num[s[i] - 'a']) * (len - i);
}
}
cout << sum << endl;
return 0;
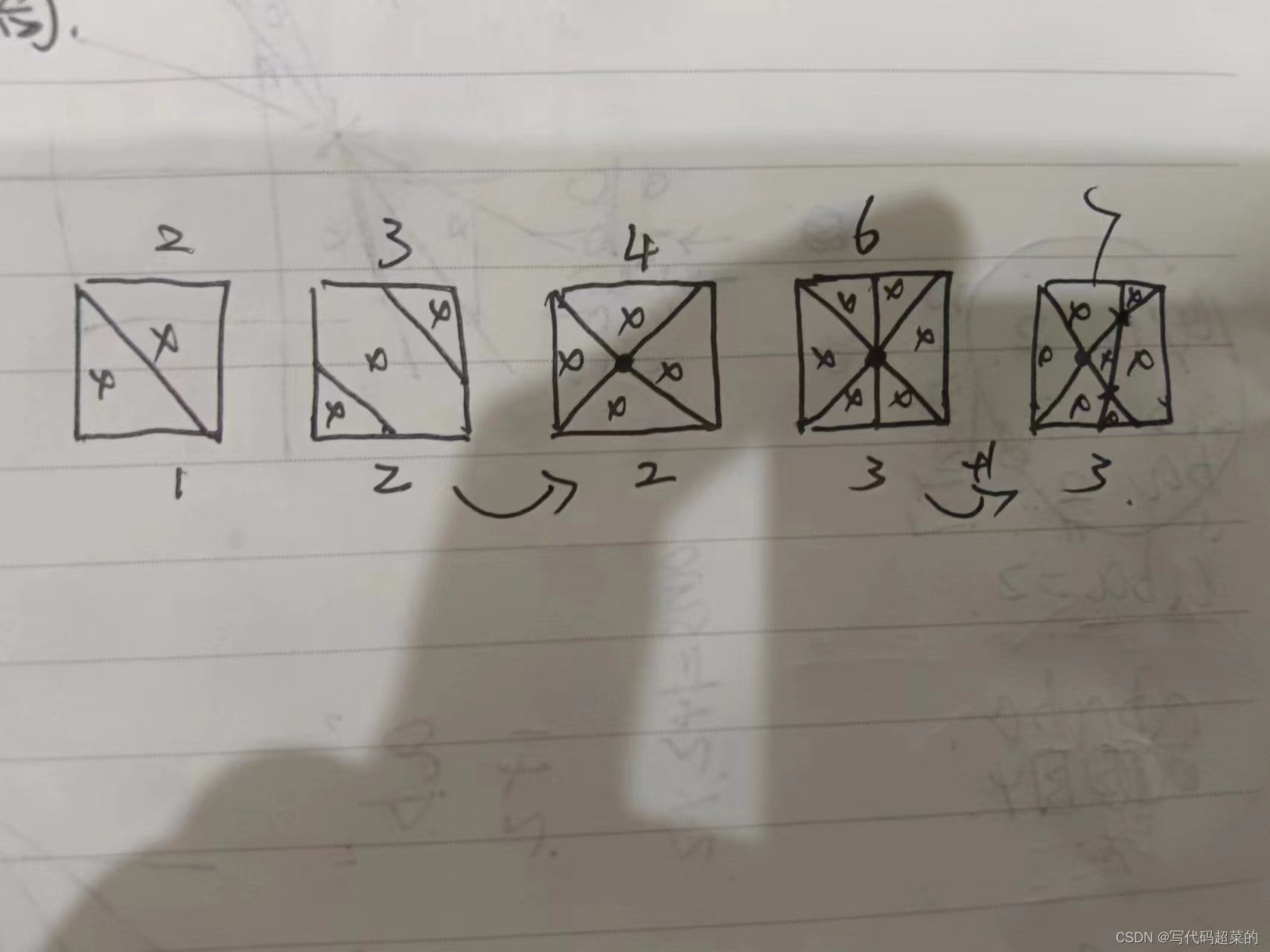
}10.平面切分

题目解析:根据下面的图片可以分析出来规律。
#include<bits/stdc++.h>
using namespace std;
const int N = 1005;
int main()
{
int n;
scanf("%d", &n);
int a, b;
long double A[N], B[N];
pair<long double, long double> p;
set<pair<long double, long double> > s; //利用set自动去重功能筛选掉重边
for(int i = 0; i < n; i++)
{
scanf("%d %d", &a, &b);
p.first = a;
p.second = b;
s.insert(p);
}
int i = 0; //将去重后的直线数据放回A,B数组
for(set<pair<long double, long double> >::iterator it = s.begin(); it != s.end(); it++, i++)
{
A[i] = it -> first;
B[i] = it -> second;
}
long long ans = 2; //初始情况当只有一条直线时,有两个平面
for(int i = 1; i < s.size(); i++) //从下标1开始,也就是第二条直线
{
set<pair<long double, long double> > pos; //记录第i条直线与先前的交点
for(int j = i-1; j >= 0; j--)
{
int a1 = A[i], b1 = B[i];
int a2 = A[j], b2 = B[j];
if(a1 == a2) //遇到平行线无交点,跳出
continue;
p.first = 1.0*(b2-b1)/(a1-a2);
p.second = 1.0*a1*((b2-b1)/(a1-a2)) + b1;
pos.insert(p);
}
ans += pos.size() + 1; //根据结论,每增加一条直线,对平面数的贡献值是其与先前直线的交点数(不重合)+1
}
printf("%d\n", ans);
return 0;
}