第1关:什么是集成学习
任务描述
本关任务:根据本节课所学知识完成本关所设置的选择题。
相关知识
为了完成本关任务,你需要掌握:1.什么是集成学习。
什么是集成学习
集成学习方法是一种常用的机器学习方法,分为bagging与boosting两种方法,应用十分广泛。集成学习基本思想是:对于一个复杂的学习任务,我们首先构造多个简单的学习模型,然后再把这些简单模型组合成一个高效的学习模型。实际上,就是“三个臭皮匠顶个诸葛亮”的道理。

集成学习采取投票的方式来综合多个简单模型的结果,按bagging投票思想,如下面例子:

假设一共训练了5个简单模型,每个模型对分类结果预测如上图,则最终预测结果为: A:2 B:3 3>2 结果为B
不过在有的时候,每个模型对分类结果的确定性不一样,即有的对分类结果非常肯定,有的不是很肯定,说明每个模型投的一票应该是有相应的权重来衡量这一票的重要性。就像在歌手比赛中,每个观众投的票记1分,而专家投票记10分。按boosting投票思想,如下例:
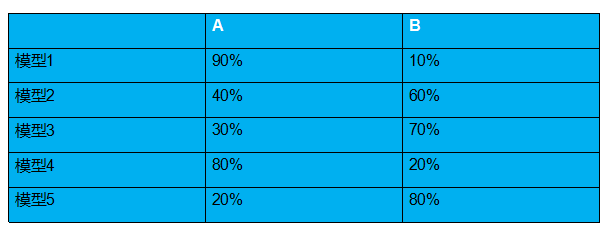
A:(0.9+0.4+0.3+0.8+0.2)/5=0.52 B:(0.1+0.6+0.7+0.2+0.8)/5=0.48 0.52>0.48 结果为A
闯关要求
根据所学知识完成右侧选择题!!!
1、对于一个二分类问题,假如现在训练了500个子模型,每个模型权重大小一样。若每个子模型正确率为51%,则整体正确率为多少?若把每个子模型正确率提升到60%,则整体正确率为多少?(C)
A、51%,60%
B、60%,90%
C、65.7%,99.99%
D、65.7%,90%第2关: Boosting
任务描述
本关任务:根据本节课所学知识完成本关所设置的选择题。 ####相关知识 为了完成本关任务,你需要掌握:1.Boosting。 #####Boosting 提升方法基于这样一种思想:对于一个复杂任务来说,将多个专家的判断进行适当的综合所得出的判断,要比其中任何一个专家单独的判断好。
历史上,Kearns和Valiant首先提出了强可学习和弱可学习的概念。指出:在PAC学习的框架中,一个概念,如果存在一个多项式的学习算法能够学习它,并且正确率很高,那么就称这个概念是强可学习的;一个概念,如果存在一个多项式的学习算法能够学习它,学习的正确率仅比随机猜测略好,那么就称这个概念是弱可学习的。非常有趣的是Schapire后来证明强可学习与弱可学习是等价的,也就是说,在PAC学习的框架下,一个概念是强可学习的充分必要条件是这个概念是弱可学习的。
这样一来,问题便成为,在学习中,如果已经发现了弱学习算法,那么能否将它提升为强学习算法。大家知道,发现弱学习算法通常要比发现强学习算法容易得多。那么如何具体实施提升,便成为开发提升方法时所要解决的问题。
与bagging不同,boosting采用的是一个串行训练的方法。首先,它训练出一个弱分类器,然后在此基础上,再训练出一个稍好点的弱分类器,以此类推,不断的训练出多个弱分类器,最终再将这些分类器相结合,这就是boosting的基本思想,流程如下图:
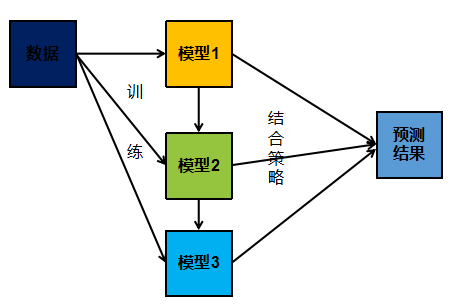
可以看出,子模型之间存在强依赖关系,必须串行生成。boosting是利用不同模型的相加,构成一个更好的模型,求取模型一般都采用序列化方法,后面的模型依据前面的模型。
1、现在有一份数据,你随机的将数据分成了n份,然后同时训练n个子模型,再将模型最后相结合得到一个强学习器,这属于boosting方法吗?(B)
A、是
B、不是
C、不确定第3关:Adaboost算法流程
任务描述
本关任务:用Python实现Adaboost,并通过鸢尾花数据集中鸢尾花的2种属性与种类对Adaboost模型进行训练。我们会调用你训练好的Adaboost模型,来对未知的鸢尾花进行分类。
相关知识
为了完成本关任务,你需要掌握:1.Adaboost算法原理,2.Adaboost算法流程。
数据集介绍

数据集为鸢尾花数据,一共有150个样本,每个样本有4个特征,由于Adaboost是一个串行的迭代二分类算法,运算成本较大,为了减轻运算成本,我们只利用其中两个特征与两种类别构造与训练模型,且adaboost算法返回的值为1与-1,所以要将标签为0的数据改为-1部分数据如下图:
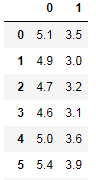
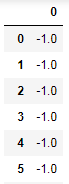
数据获取代码:
#获取并处理鸢尾花数据def create_data():iris = load_iris()df = pd.DataFrame(iris.data, columns=iris.feature_names)df['label'] = iris.targetdf.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']data = np.array(df.iloc[:100, [0, 1, -1]])#将标签为0的数据标签改为-1for i in range(len(data)):if data[i,-1] == 0:data[i,-1] = -1return data[:,:2], data[:,-1]
Adaboost算法原理
对提升方法来说,有两个问题需要回答:一是在每一轮如何改变训练数据的权值或概率分布;二是如何将弱分类器组合成一个强分类器。关于第1个问题,AdaBoost的做法是,提高那些被前一轮弱分类器错误分类样本的权值,而降低那些被正确分类样本的权值。这样一来,那些没有得到正确分类的数据,由于其权值的加大而受到后一轮的弱分类器的更大关注。于是,分类问题被一系列的弱分类器“分而治之”。至于第2个问题,即弱分类器的组合,AdaBoost采取加权多数表决的方法,加大分类误差率小的弱分类器的权值,使其在表决中起较大的作用,减小分类误差率大的弱分类器的权值,使其在表决中起较小的作用。
Adaboost算法流程
AdaBoost是AdaptiveBoost的缩写,表明该算法是具有适应性的提升算法。
算法的步骤如下:
1.给每个训练样本(x1,x2,..,xN)分配权重,初始权重w1均为1/N
2.针对带有权值的样本进行训练,得到模型Gm(初始模型为$$G _1$$)
3.计算模型Gm的误分率:
em=i∑NwiI(yi=GM(Xi))
其中:
I(yi=GM(Xi)
为指示函数,表示括号内成立时函数值为1,否则为0
4.计算模型Gm的系数:
αm=21log[em1−em]
5.根据误分率e和当前权重向量wm更新权重向量:
wm+1,i=zmwmexp(−αmyiGm(xi))
其中Zm为规范化因子:
zm=i=1∑mwmiexp(−αmyiGm(xi))
6.计算组合模型f(x)=∑m=1MαmGm(xi)的误分率
7.当组合模型的误分率或迭代次数低于一定阈值,停止迭代;否则,回到步骤 2
编程要求
根据提示,在右侧编辑器补充 Python 代码,实现Adaboost算法,并利用训练好的模型对鸢尾花数据进行分类。
测试说明
只需返回分类结果即可,程序内部会检测您的代码,预测正确率高于95%视为过关。
#encoding=utf8
import numpy as np
#adaboost算法
class AdaBoost:
'''
input:n_estimators(int):迭代轮数
learning_rate(float):弱分类器权重缩减系数
'''
def __init__(self, n_estimators=50, learning_rate=1.0):
self.clf_num = n_estimators
self.learning_rate = learning_rate
def init_args(self, datasets, labels):
self.X = datasets
self.Y = labels
self.M, self.N = datasets.shape
# 弱分类器数目和集合
self.clf_sets = []
# 初始化weights
self.weights = [1.0/self.M]*self.M
# G(x)系数 alpha
self.alpha = []
def _G(self, features, labels, weights):
'''
input:features(ndarray):数据特征
labels(ndarray):数据标签
weights(ndarray):样本权重系数
'''
#********* Begin *********#
m = len(features)
error = 100000.0 # 无穷大
beat_v = 0.0
#单维features
features_min = min(features)
features_max = max(features)
n_step = (features_max-features_min+self.learning_rate) // self.learning_rate
direct,compare_array = None,None
for i in range(1,int(n_step)):
v = features_min + self.learning_rate * i
if v not in features:
# 误分类计算
compare_array_positive = np.array(
[1 if features[k] > v else -1 for k in range(m)])
weight_error_positive = sum([
weights[k] for k in range(m)
if compare_array_positive[k] != labels[k]
])
compare_array_nagetive = np.array(
[-1 if features[k] > v else 1 for k in range(m)])
weight_error_nagetive = sum([
weights[k] for k in range(m)
if compare_array_nagetive[k] != labels[k]
])
if weight_error_positive < weight_error_nagetive:
weight_error = weight_error_positive
_compare_array = compare_array_positive
direct = 'positive'
else:
weight_error = weight_error_nagetive
_compare_array = compare_array_nagetive
direct = 'nagetive'
# print('v:{} error:{}'.format(v, weight_error))
if weight_error < error:
error = weight_error
compare_array = _compare_array
best_v = v
return best_v, direct, error, compare_array
# 计算alpha
def _alpha(self, error):
return 0.5 * np.log((1 - error) / error)
# 规范化因子
def _Z(self, weights, a, clf):
return sum([
weights[i] * np.exp(-1 * a * self.Y[i] * clf[i])
for i in range(self.M)
])
# 权值更新
def _w(self, a, clf, Z):
for i in range(self.M):
self.weights[i] = self.weights[i] * np.exp(
-1 * a * self.Y[i] * clf[i]) / Z
# G(x)的线性组合
def _f(self, alpha, clf_sets):
pass
def G(self, x, v, direct):
if direct == 'positive':
return 1 if x > v else -1
else:
return -1 if x > v else 1
def fit(self, X, y):
self.init_args(X, y)
for epoch in range(self.clf_num):
axis = 0
final_direct = 'null'
best_clf_error, best_v, clf_result = 100000, None, None
# 根据特征维度, 选择误差最小的
for j in range(self.N):
features = self.X[:, j]
# 分类阈值,分类误差,分类结果
v, direct, error, compare_array = self._G(
features, self.Y, self.weights)
if error < best_clf_error:
best_clf_error = error
best_v = v
final_direct = direct
clf_result = compare_array
axis = j # axis数字代表第几个属性列
# print('epoch:{}/{} feature:{} error:{} v:{}'.format(epoch, self.clf_num, j, error, best_v))
if best_clf_error == 0:
break
# 计算G(x)系数a
a = self._alpha(best_clf_error)
self.alpha.append(a)
# 记录分类器
self.clf_sets.append((axis, best_v, final_direct))
# 规范化因子
Z = self._Z(self.weights, a, clf_result)
# 权值更新
self._w(a, clf_result, Z)
#********* End *********#
def predict(self, feature):
result = 0.0
for i in range(len(self.clf_sets)):
axis, clf_v, direct = self.clf_sets[i]
f_input = feature[axis]
result += self.alpha[i] * self.G(f_input, clf_v, direct)
# sign
return 1 if result > 0 else -1
def score(self, X_test, y_test):
right_count = 0
for i in range(len(X_test)):
feature = X_test[i]
if self.predict(feature) == y_test[i]:
right_count += 1
return right_count / len(X_test)
第4关:sklearn中的Adaboost
任务描述
本关任务:你需要调用sklearn中的Adaboost模型,并通过鸢尾花数据集中鸢尾花的2种属性与种类对Adaboost模型进行训练。我们会调用你训练好的Adaboost模型,来对未知的鸢尾花进行分类。
相关知识
为了完成本关任务,你需要掌握:1.AdaBoostClassifier。
数据介绍

数据集为鸢尾花数据,一共有150个样本,每个样本有4个特征,由于Adaboost是一个串行的迭代二分类算法,运算成本较大,为了减轻运算成本,我们只利用其中两个特征与两种类别构造与训练模型,且adaboost算法返回的值为1与-1,所以要将标签为0的数据改为-1部分数据如下图:


数据获取代码:
#获取并处理鸢尾花数据def create_data():iris = load_iris()df = pd.DataFrame(iris.data, columns=iris.feature_names)df['label'] = iris.targetdf.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']data = np.array(df.iloc[:100, [0, 1, -1]])#将标签为0的数据标签改为-1for i in range(len(data)):if data[i,-1] == 0:data[i,-1] = -1return data[:,:2], data[:,-1]
AdaBoostClassifier
AdaBoostClassifier 的构造函数中有四个常用的参数可以设置:
algorithm:这个参数只有 AdaBoostClassifier 有。主要原因是scikit-learn 实现了两种 Adaboost 分类算法,SAMME和SAMME.R。两者的主要区别是弱学习器权重的度量,SAMME.R使用了概率度量的连续值,迭代一般比SAMME快,因此 AdaBoostClassifier 的默认算法algorithm的值也是SAMME.R。n_estimators:弱学习器的最大迭代次数。一般来说n_estimators太小,容易欠拟合,n_estimators太大,又容易过拟合,一般选择一个适中的数值。默认是50。learning_rate: AdaBoostClassifier 和 AdaBoostRegressor 都有,即每个弱学习器的权重缩减系数ν,默认为1.0。base_estimator:弱分类学习器或者弱回归学习器。理论上可以选择任何一个分类或者回归学习器,不过需要支持样本权重。我们常用的一般是 CART 决策树或者神经网络 MLP。
和sklearn中其他分类器一样,AdaBoostClassifier 类中的fit函数用于训练模型,fit函数有两个向量输入:
X:大小为**[样本数量,特征数量]**的ndarray,存放训练样本Y:值为整型,大小为[样本数量]的ndarray,存放训练样本的分类标签
AdaBoostClassifier 类中的predict函数用于预测,返回预测标签,predict函数有一个向量输入:
X:大小为**[样本数量,特征数量]**的ndarray,存放预测样本 AdaBoostClassifier的使用代码如下:
ada=AdaBoostClassifier(n_estimators=5,learning_rate=1.0)ada.fit(train_data,train_label)predict = ada.predict(test_data)
编程要求
填写ada_classifier(train_data,train_label,test_data)函数完成鸢尾花分类任务,其中:
train_data:训练样本train_label:训练标签test_data:测试样本
测试说明
只需返回预测结果即可,程序内部会检测您的代码,预测正确率高于95%视为过关。
#encoding=utf8
from sklearn.tree import DecisionTreeClassifier
from sklearn.ensemble import AdaBoostClassifier
def ada_classifier(train_data,train_label,test_data):
'''
input:train_data(ndarray):训练数据
train_label(ndarray):训练标签
test_data(ndarray):测试标签
output:predict(ndarray):预测结果
'''
#********* Begin *********#
ada=AdaBoostClassifier(base_estimator=DecisionTreeClassifier
(max_depth=2,min_samples_split=10,min_samples_leaf=5),
n_estimators=50,learning_rate=0.2)
ada.fit(train_data,train_label)
predict=ada.predict(test_data)
#********* End *********#
return predict