最大二叉树
给定一个不含重复元素的整数数组。一个以此数组构建的最大二叉树定义如下:
- 二叉树的根是数组中的最大元素。
- 左子树是通过数组中最大值左边部分构造出的最大二叉树。
- 右子树是通过数组中最大值右边部分构造出的最大二叉树。
通过给定的数组构建最大二叉树,并且输出这个树的根节点。
示例 :

1 <= nums.length <= 1000
0 <= nums[i] <= 1000
nums 中的所有整数 互不相同
构造过程如下:

构造树一般采用的是前序遍历,因为先构造中间节点,然后递归构造左子树和右子树;
遍历第一步,确定函数参数和返回值:
参数传入的是存放元素的数组,返回该数组构造的二叉树的头结点,返回类型是指向节点的指针:
TreeNode* constructMaximumBinaryTree(vector<int>& nums)
遍历第二步:
确定终止条件,由于本题要求是用数组构建,且题目给出数组的长度大于等于一,所以不用考虑数组非空的情况;
当数组长度为一时,说明此时遍历到了叶子节点,此时定义新节点并返回节点;
TreeNode* node = new TreeNode(0);
if (nums.size() == 1) {
node->val = nums[0];
return node;
}
遍历第三步:
确定单层遍历条件:
由于需要数组最大值作为根节点,所以优先遍历整个数组获取最大值作为根节点,并得到这个最大值的下标作为分割边界;思路可以参考之前刚做过的中序后序构建二叉树一致,可以用新数组vector,也可以直接传入函数时定义两个int型变量记录左右区间,这里保持函数定义一致以vector型为例,若考虑代码性能选择后者;
int MaxValue = 0;//获得数组最大值,由于题目给出条件数组为非负自然数,所以此处无须定义为INT_MIN
int Index = 0;//定义最大值下标
for(int i = 0; i < right - left/*nums.size()*/; i++){//遍历完毕,获得最大值
if(nums[i] > MaxValue){
MaxValue = nums[i];
Index = i;
}
}
TreeNode* node = new TreeNode(0);
node->val = MaxValue;
/*上述代码为"中"的处理过程*/
if(Index > 0){//左子树不为空
vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
node->left = constructMaximumBinaryTree(newVec);
}
if(nums.size()- Index - 1 > 0){//右子树不为空
vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
node->right = constructMaximumBinaryTree(newVec);
}
整体代码如下:
class Solution {
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
TreeNode* node = new TreeNode(0);
if (nums.size() == 1) {
node->val = nums[0];
return node;
}
// 找到数组中最大的值和对应的下标
int maxValue = 0;
int maxValueIndex = 0;
for (int i = 0; i < nums.size(); i++) {
if (nums[i] > maxValue) {
maxValue = nums[i];
maxValueIndex = i;
}
}
node->val = maxValue;
// 最大值所在的下标左区间 构造左子树
if (maxValueIndex > 0) {
vector<int> newVec(nums.begin(), nums.begin() + maxValueIndex);
node->left = constructMaximumBinaryTree(newVec);
}
// 最大值所在的下标右区间 构造右子树
if (maxValueIndex < (nums.size() - 1)) {
vector<int> newVec(nums.begin() + maxValueIndex + 1, nums.end());
node->right = constructMaximumBinaryTree(newVec);
}
return node;
}
};
提升代码性能,重写函数,整体代码如下:
class Solution{
private:
TreeNode* traversal(vector<int>& nums, int left, int right){
if(left >= right) return NULL;
// 分割点下标:maxValueIndex
int maxValueIndex = left;
for (int i = left + 1; i < right; ++i) {//理解递归思路
if (nums[i] > nums[maxValueIndex]) maxValueIndex = i;
}
TreeNode* root = new TreeNode(nums[maxValueIndex]);
// 左闭右开:[left, maxValueIndex)
//无须判断节点是否为空,因为可以允许空节点进入
root->left = traversal(nums, left, maxValueIndex);
// 左闭右开:[maxValueIndex + 1, right)
root->right = traversal(nums, maxValueIndex + 1, right);
return root;
}
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums){
return traversal(nums, 0, nums.size());
}
};
合并二叉树
给定两个二叉树,想象当你将它们中的一个覆盖到另一个上时,两个二叉树的一些节点便会重叠。
你需要将他们合并为一个新的二叉树。合并的规则是如果两个节点重叠,那么将他们的值相加作为节点合并后的新值,否则不为 NULL 的节点将直接作为新二叉树的节点。
示例 1:

注意: 合并必须从两个树的根节点开始。
看起来操作两个二叉树第一次见,实际上在对称二叉树中已经使用过类似的思路了;
合并二叉树,只需要同时遍历两个二叉树就可以了:
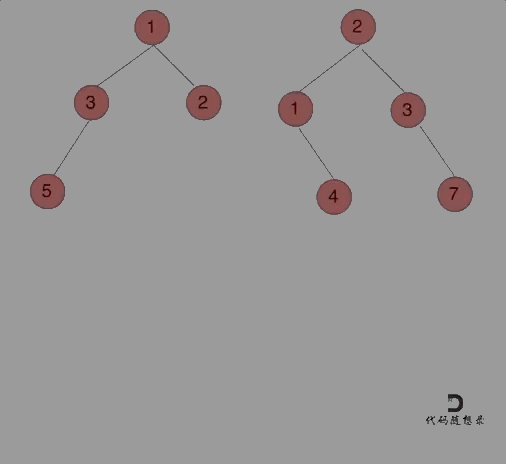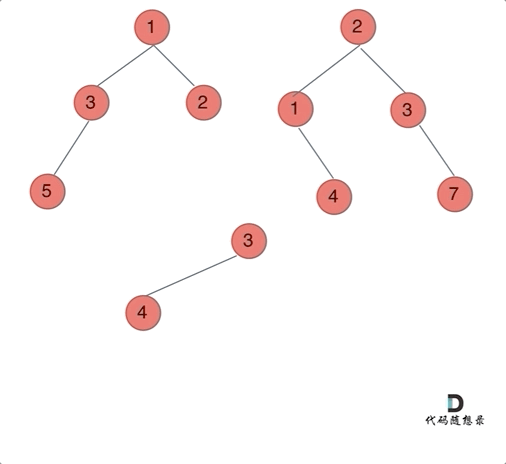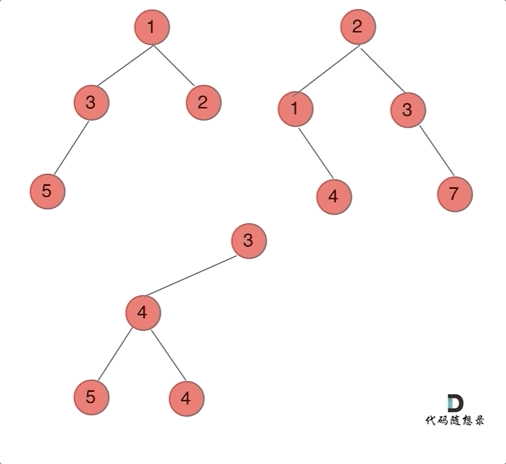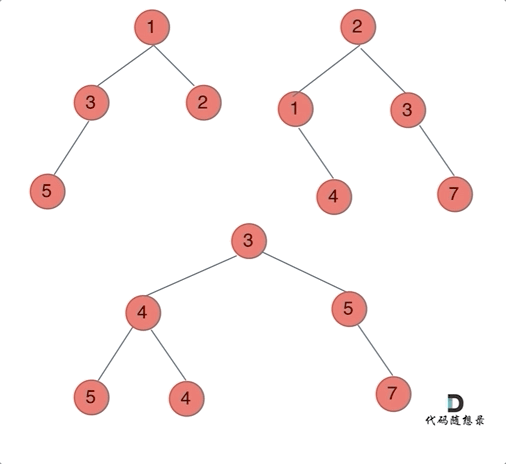
代码实现(前序)如下:
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == NULL) return t2; // 如果t1为空,合并之后就应该是t2
if (t2 == NULL) return t1; // 如果t2为空,合并之后就应该是t1
// 修改了t1的数值和结构
t1->val += t2->val; // 中
t1->left = mergeTrees(t1->left, t2->left); // 左
t1->right = mergeTrees(t1->right, t2->right); // 右
return t1;
}
};
本题前中后序都是可以的,前序最好理解;
也可以采取构造新节点的方法:
class Solution {
public:
TreeNode* mergeTrees(TreeNode* t1, TreeNode* t2) {
if (t1 == NULL) return t2;
if (t2 == NULL) return t1;
// 重新定义新的节点,不修改原有两个树的结构
TreeNode* root = new TreeNode(0);
root->val = t1->val + t2->val;
root->left = mergeTrees(t1->left, t2->left);
root->right = mergeTrees(t1->right, t2->right);
return root;
}
};
二叉搜索树中的搜索
给定二叉搜索树(BST)的根节点和一个值。 你需要在BST中找到节点值等于给定值的节点。 返回以该节点为根的子树。 如果节点不存在,则返回 NULL。
例如,

在上述示例中,如果要找的值是 5,但因为没有节点值为 5,我们应该返回 NULL。
二叉搜索树是一个有序树:
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
它的左、右子树也分别为二叉搜索树;
。
例如,
[外链图片转存中…(img-V4uavmvL-1712591045263)]
在上述示例中,如果要找的值是 5,但因为没有节点值为 5,我们应该返回 NULL。
二叉搜索树是一个有序树:
若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
它的左、右子树也分别为二叉搜索树;
这就决定了,二叉搜索树,递归遍历和迭代遍历和普通二叉树都不一样;
但是因为有序这一特性的存在,代码写起来是很简洁的;
TreeNode* searchBST(TreeNode* root, int val){//函数参数和返回值
//终止条件
if(root == NULL || root->val == val) return root;//中
if(root->val > val) return searchBST(root->left, val);//左
if(root->val < val) return searchBST(root->right, val);//右
return NULL;
}
也可以用迭代法实现:
TreeNode* searchBST(TreeNode* root, int val){
while(root != NULL){
if(root->val > val) root = root->left;
else if(root->val < val) root = root->right;
else return root;
}
return NULL;
}
验证二叉搜索树
给定一个二叉树,判断其是否是一个有效的二叉搜索树。
假设一个二叉搜索树具有如下特征:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。

直观想法:中序遍历二叉树,判断数组是否递增即可;
vector<int> res;
bool traversal(TreeNode* root){
if(root == NULL) return true;//空节点什么二叉树都是
isBST(root->left);
res.push_back(root->val);
isBST(root->right);
}
traversal(root);
for (int i = 1; i < vec.size(); i++) {
// 注意要小于等于,搜索树里不能有相同元素
if (vec[i] <= vec[i - 1]) return false;
}
return true;
若不使用数组辅助直接对二叉树进行操作,如何判断?
很直白的一个想法
if(root->val > root->left->val && root->val < root->right->val) return ture;
**这么写就错了!**因为需要满足的不仅是大于子节点数值,而是整个子树节点的元素;
这里可以采取一个最小值的全局变量,也可以直接使用双指针的思路来优化:
class Solution {
public:
TreeNode* pre = NULL;
bool isValidBST(TreeNode* root){
if(root == NULL) return true;
bool left = isValidBST(root->left);
if(pre != NULL && pre->val >= root->val) return false;//当前一个节点大于等于后一个节点的时候,return false;
pre = root;//记录前一个节点
bool right = isValidBST(root->right);
return left && right;
}
};