给出节点个数n, edges是连接的边，[a,b]是连接的两个顶点。
hasApple表示第 i 个顶点上是否有苹果。

走一条边需要耗时1s, 从顶点0出发，最后回到顶点0,
问收集所有苹果所需最短的时间。

思路：

（1）DFS

可以把问题简化一下，
如果一个顶点，它的child有苹果，这个点必然会耗时2，因为要经过它进入child, 还要经过它返回顶点0.

如果一个顶点，它自己有苹果，那么也要耗时2，因为要走向它，还要返回上一级。

那么就可以DFS遍历，从叶子节点开始递归返回，child有苹果，+2，自己有苹果+2.
还要用一个visited记录每个节点是否已经被访问过。
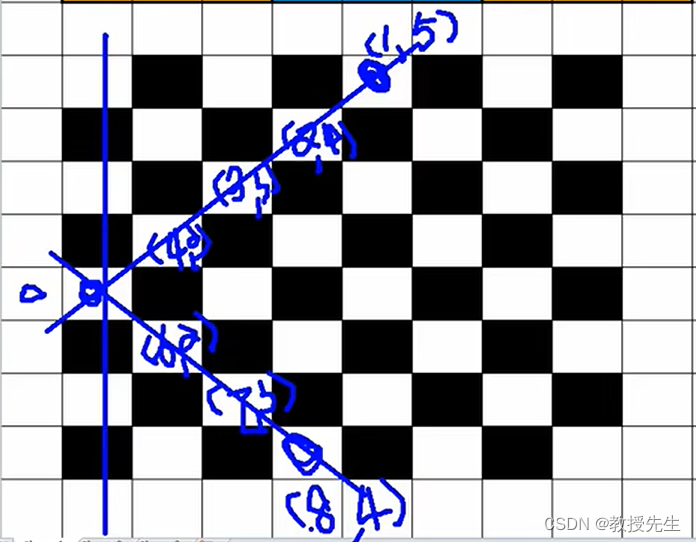
例如图中的节点1，在进入4时它已经被访问过了，那么再进入5时它就不需要再+2。

出发点是0，所以节点0不需要+2.

该方法需要构建无向图。

class Solution {
    HashMap<Integer,List<Integer>> graph = new HashMap<>();
    HashSet<Integer> visited = new HashSet<>();

    public int minTime(int n, int[][] edges, List<Boolean> hasApple) {

        //make graph
        for(int[] edge : edges) {
            graph.putIfAbsent(edge[0], new LinkedList<>());
            graph.putIfAbsent(edge[1], new LinkedList<>());
            graph.get(edge[0]).add(edge[1]);
            graph.get(edge[1]).add(edge[0]);
        }

        return dfs(0, hasApple);
    }

    int dfs(int node, List<Boolean> hasApple) {
        visited.add(node);
        int res = 0;

        for(int child : graph.getOrDefault(node, new LinkedList<>())) {
            if(visited.contains(child)) continue;
            res += dfs(child, hasApple); 
        }

        if((res > 0 || hasApple.get(node)) && node > 0) res += 2;

        return res;
    }

（2）类似 Union-Find

前面已经说过，2种情况，

节点的child有苹果，时间+2，
节点自己有苹果，时间+2，
节点0除外，已访问过的节点除外。

刚刚的DFS是从上往下，但是是从下往上递归。

那是不是可以直接从下往上呢？

只需记录每个节点的parent, 然后从节点开始，不断访问它的parent,
节点自己有苹果，时间+2，同时它所有的parent的时间+2，
已访问过的和节点0除外。

    public int minTime(int n, int[][] edges, List<Boolean> hasApple) {

        int[] parent = new int[n];
        Arrays.fill(parent, -1);
        
        // Build tree like structure with each child pointing to its parent node
        // edge[0] is parent by default for edge[1]. 
        // If edge[1] is already assigned a parent, then make edge[1] a parent of edge[0]
        parent[0] = 0;
        for (int[] edge : edges) {
            if (parent[edge[1]] == -1) {
                parent[edge[1]] = edge[0];
            } else {
                parent[edge[0]] = edge[1];
            }
        }

        int timeSpent = 0;
        boolean[] visited = new boolean[n];
        visited[0] = true;

        for (int node = 1; node < n; ++node) {
            if (hasApple.get(node)) {
                for (int parentNode = node; !visited[parentNode]; parentNode = parent[parentNode]) {
                    visited[parentNode] = true;
                    timeSpent += 2;
                }
            }
        }

        return timeSpent;
    }