Leetcode算法训练日记 | day17

news2024/7/4 23:46:16

一、平衡二叉树

1.题目

Leetcode：第 110 题

给定一个二叉树，判断它是否是 平衡二叉树

示例 1：

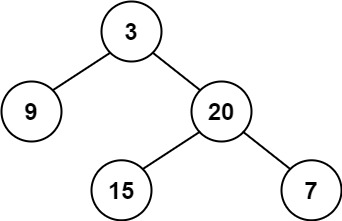
输入：root = [3,9,20,null,null,15,7]
输出：true

示例 2：

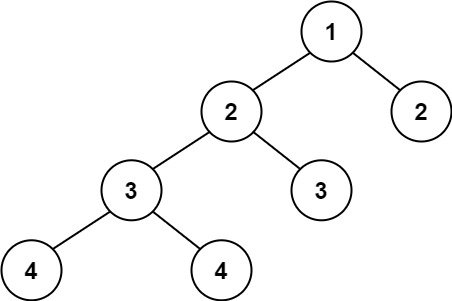
输入：root = [1,2,2,3,3,null,null,4,4]
输出：false

示例 3：

输入：root = []
输出：true

2.解题思路

使用递归法和迭代法遍历二叉树，对于每个节点，计算其左右子树的深度差。如果深度差大于1，则树不平衡，返回false。如果遍历结束，没有发现深度差大于1的情况，则树是平衡的，返回true。

3.实现代码

#include <iostream>
#include <vector>
#include <queue>
#include <stack>
using namespace std;

// 定义一个结构体TreeNode，用于表示二叉树的节点。
struct TreeNode {
    int val; // 存储节点的值。
    TreeNode* left; // 指向该节点左子树的指针。
    TreeNode* right; // 指向该节点右子树的指针。
    // TreeNode的构造函数，用于创建一个TreeNode实例。
    // 参数x是节点的值，left和right默认为NULL，表示没有左右子节点。
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

// 一、判断平衡二叉树（递归法）
class Solution1 {
public:
    // 定义名为getHeight的辅助函数，用于计算二叉树节点的高度。
    // 同时，该函数会检查子树的高度差是否不超过1，以此判断树是否平衡。
    // 函数接受一个参数：指向二叉树节点的指针node。
    int getHeight(TreeNode* node) {
        if (node == NULL) return 0; // 如果传入的节点为空，说明是一棵空树，返回高度0。

        int leftHeiht = getHeight(node->left);  // 递归地计算左子树节点的高度。
        if (leftHeiht == -1) return -1; // 如果左子树高度计算结果为-1，说明左子树不平衡，直接返回-1。

        int rightHeiht = getHeight(node->right);// 递归地计算右子树节点的高度。
        if (rightHeiht == -1) return -1;// 如果右子树高度计算结果为-1，说明右子树不平衡，直接返回-1。

        
        int heightDiff = abs(leftHeiht - rightHeiht);// 计算左右子树的高度差。
        if (heightDiff > 1) return -1;// 如果高度差大于1，说明当前节点的子树不平衡，返回-1。
        // 如果子树平衡，返回当前节点的高度，为左右子树的最大高度加1（当前节点本身的高度）。
        return 1 + max(leftHeiht, rightHeiht);
    }
    // 定义名为isBalanced的成员函数，用于判断二叉树是否平衡。
    // 函数接受一个参数：指向二叉树根节点的指针root。
    bool isBalanced(TreeNode* root) {
        // 调用getHeight函数计算根节点的高度，如果返回值为-1，说明树不平衡，返回false。
        // 否则，返回true，表示树是平衡的。
        return getHeight(root) == -1 ? false : true;
    }
};


// 二、判断平衡二叉树（迭代法）
class Solution2 {
public:
    // getDepth函数用于计算二叉树的深度。
    // 函数接受一个参数：指向二叉树节点的指针cur。
    int getDepth(TreeNode* cur) {
        stack<TreeNode*> st; // 创建一个栈st，用于存储遍历过程中的节点。
        if (cur != NULL) st.push(cur); // 如果当前节点cur不为空，则将其压入栈中。
        int depth = 0; // 初始化深度计数器为0。
        int result = 0;  // 初始化最大深度计数器为0。

        while (!st.empty()) {// 使用while循环遍历栈不为空时的所有节点。
            TreeNode* node = st.top(); // 获取栈顶节点。
            if (node != NULL) {// 如果节点不为空，则执行以下操作：
                st.pop(); // 将当前节点从栈中弹出。
                st.push(node); // 将当前节点压入栈中，以便后续处理。
                st.push(NULL);// 将一个空指针压入栈中，作为左右子树遍历的分隔符。
                depth++;// 深度计数器加1。

                if (node->right) st.push(node->right); // 如果节点有右子节点，将其压入栈中。
                if (node->left) st.push(node->left);// 如果节点有左子节点，将其压入栈中。
            }

            else { // 如果节点为空，说明已经到达了叶子节点的下方，执行以下操作：
                st.pop();// 弹出空指针
                node = st.top();//获取节点
                st.pop();//弹出节点
                depth--;// 节点计数器减1。
            }
            // 更新最大深度计数器，取当前最大值。
            result = result > depth ? result : depth;
        }
        return result;// 返回最大深度。
    }

    // isBalanced函数用于判断二叉树是否平衡。
    // 函数接受一个参数：指向二叉树根节点的指针root。
    bool isBalanced(TreeNode* root) {
        stack<TreeNode*> st;   // 创建一个栈st，用于存储遍历过程中的节点。
        if (root == NULL) return true; // 如果根节点root为空，说明是一棵空树，返回true。
        st.push(root); // 将根节点压入栈中。

        while (!st.empty()) { // 使用while循环遍历栈不为空时的所有节点。
            TreeNode* node = st.top();  // 获取栈顶节点
            st.pop();// 弹出当前节点。
            // 计算当前节点的左右子树深度差。
            int depthDiff = abs(getDepth(node->left) - getDepth(node->right));
            if (depthDiff > 1) { // 如果左右子树深度差大于1，说明树不平衡，返回false。
                return false;
            }
            if (node->left) st.push(node->left); // 如果栈顶节点有左子节点，将其压入栈中。
            if (node->right) st.push(node->right);// 如果栈顶节点有右子节点，将其压入栈中。
        }
        return true; // 如果遍历结束，说明树是平衡的，返回true。
    }
};

//测试
// 辅助函数，用于创建一个新的TreeNode
TreeNode* createNode(int value) {
    return new TreeNode(value);
}

// 辅助函数，用于构建二叉树
TreeNode* buildTree(vector<int>& values) {
    if (values.empty()) return NULL;
    TreeNode* root = createNode(values[0]);
    queue<TreeNode*> queueNode;
    queueNode.push(root);
    int i = 1;
    while (!queueNode.empty()) {
        TreeNode* node = queueNode.front();
        queueNode.pop();
        if (i < values.size()) {
            node->left = createNode(values[i++]);
            queueNode.push(node->left);
        }
        if (i < values.size()) {
            node->right = createNode(values[i++]);
            queueNode.push(node->right);
        }
    }
    return root;
}

// 打印容器中的所有元素，用于验证测试结果
void printVector(const vector<int>& vec) {
    for (int value : vec) {
        cout << value << " ";
    }
    cout << endl;
}

// 主函数
int main() {

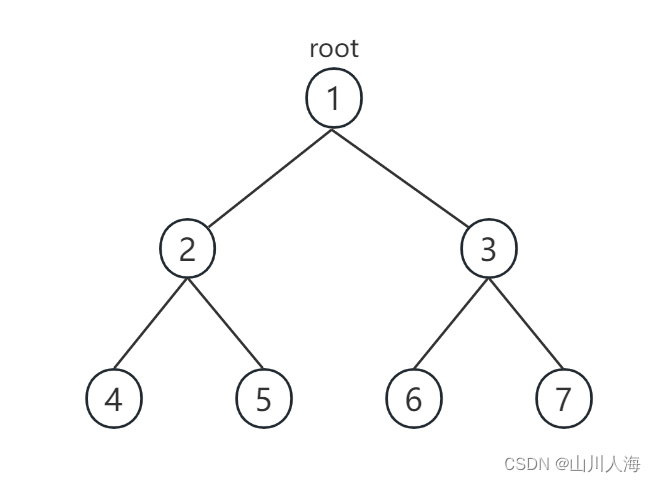
    vector<int> treeValues = { 1, 2, 3, 4, 5, 6, 7 };// 定义二叉树的层序遍历结果，用于构建二叉树
    TreeNode* root = buildTree(treeValues); // 构建二叉树
    Solution1 s1;// 创建Solution类的实例
    Solution2 s2;
    int result1 = s1.isBalanced(root);// 传入二叉树的根节点
    int result2 = s2.isBalanced(root);
    cout << "判断平衡二叉树（递归法）结果是: " << result1 << endl;
    cout << endl;
    cout << "判断平衡二叉树（迭代法）结果是：" << result2 << endl;
    cout << endl;
    return 0;
}

二、二叉树的所有路径

1.题目

Leetcode：第 257 题

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

示例 1：

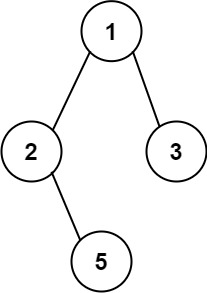
输入：root = [1,2,3,null,5]
输出：["1->2->5","1->3"]

示例 2：

输入：root = [1]
输出：["1"]
2.解题思路

使用递归法和迭代法遍历二叉树所有节点，记录遍历的路径。

3.实现代码
#include <iostream>
#include <vector>
#include <queue>
#include <stack>
#include <string>
using namespace std;

// 定义一个结构体TreeNode，用于表示二叉树的节点。
struct TreeNode {
    int val; // 存储节点的值。
    TreeNode* left; // 指向该节点左子树的指针。
    TreeNode* right; // 指向该节点右子树的指针。
    // TreeNode的构造函数，用于创建一个TreeNode实例。
    // 参数x是节点的值，left和right默认为NULL，表示没有左右子节点。
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

// 一、二叉树的所有路径（递归法）
class Solution1 {
public:
    // traversal函数用于递归遍历二叉树并收集所有从根到叶子节点的路径。
    // cur是当前遍历到的节点，path是用于记录当前路径的容器，result是存储所有路径的容器。
    void traversal(TreeNode* cur, vector<int>& path, vector<string>& result) {
        path.push_back(cur->val); // 将当前节点的值添加到路径容器的末尾,这样做是为了确保最后一个节点也会被加入到路径中。
        if (cur->left == NULL && cur->right == NULL) { // 检查当前节点是否为叶子节点（没有左右子节点）。
            string sPath;// 当到达叶子节点时，构造并保存当前路径的字符串表示。

            // 遍历路径容器，将每个节点的值转换为字符串并拼接，节点之间用"->"连接。
            for (int i = 0; i < path.size() - 1; i++) {
                sPath += to_string(path[i]);
                sPath += "->";
            }
            
            sPath += to_string(path[path.size() - 1]);// 将最后一个节点的值添加到路径字符串的末尾。
            result.push_back(sPath);// 将构造好的路径字符串添加到结果集中。
            return;// 到达叶子节点后，返回继续遍历其他分支。
        }
       
        if (cur->left) { 
            traversal(cur->left, path, result); // 如果当前节点有左子节点，递归遍历左子树。
            path.pop_back();// 在回溯时，从路径中移除当前节点，以便探索其他分支。
        }
        
        if (cur->right) {
            traversal(cur->right, path, result); // 如果当前节点有右子节点，递归遍历右子树。
            path.pop_back();// 同样，在回溯时从路径中移除当前节点。
        }
    }

    // binaryTreePaths函数用于返回二叉树的所有根到叶子节点的路径。
    // root是二叉树的根节点。
    vector<string> binaryTreePaths(TreeNode* root) {
        
        vector<string> result;// 初始化一个空的字符串容器，用于存储所有路径的字符串表示。
        vector<int> path;// 初始化一个空的整数容器，用于记录当前路径。
        if (root == NULL) return result;// 如果根节点为空，则直接返回空的路径列表。
        traversal(root, path, result);// 调用traversal函数开始递归遍历，传入根节点、路径容器和结果容器。
        return result;// 返回包含所有路径的字符串容器。
    }
};

// 一、二叉树的所有路径（迭代法）
class Solution2 {
public:
    // binaryTreePaths函数用于返回二叉树的所有路径。
    // root是二叉树的根节点。
    vector<string> binaryTreePaths(TreeNode* root) {
        stack<TreeNode*> treeSt; // 创建一个栈treeSt，用于保存树的遍历节点。
        stack<string> pathSt;// 创建一个栈pathSt，用于保存遍历路径的节点。
        vector<string> result;// 创建一个字符串向量result，用于保存最终路径集合。
        if (root == NULL) return result;// 如果根节点为空，直接返回空的路径列表。
        treeSt.push(root);// 将根节点入treeSt栈，同时将根节点的值入pathSt栈。
        pathSt.push(to_string(root->val));
        
        while (!treeSt.empty()) {// 使用while循环遍历栈不为空时的所有节点。
            // 取出treeSt栈顶的节点，
            TreeNode* node = treeSt.top();
            treeSt.pop(); 

            // 取出pathSt栈顶的路径字符串。
            string path = pathSt.top(); 
            pathSt.pop();

            // 如果当前节点是叶子节点，将路径字符串添加到结果列表中。
            if (node->left == NULL && node->right == NULL) {
                result.push_back(path);
            }

            // 如果当前节点有右子节点，将其入treeSt栈，并更新对应的路径。
            if (node->right) {
                treeSt.push(node->right);
                pathSt.push(path + "->" + to_string(node->right->val));
            }

            // 如果当前节点有左子节点，将其入treeSt栈，并更新对应的路径。
            if (node->left) {
                treeSt.push(node->left);
                pathSt.push(path + "->" + to_string(node->left->val));
            }
        }
        // 返回包含所有路径的字符串向量。
        return result;
    }
};

//测试
// 辅助函数，用于创建一个新的TreeNode
TreeNode* createNode(int value) {
    return new TreeNode(value);
}

// 辅助函数，用于构建二叉树
TreeNode* buildTree(vector<int>& values) {
    if (values.empty()) return NULL;
    TreeNode* root = createNode(values[0]);
    queue<TreeNode*> queueNode;
    queueNode.push(root);
    int i = 1;
    while (!queueNode.empty()) {
        TreeNode* node = queueNode.front();
        queueNode.pop();
        if (i < values.size()) {
            node->left = createNode(values[i++]);
            queueNode.push(node->left);
        }
        if (i < values.size()) {
            node->right = createNode(values[i++]);
            queueNode.push(node->right);
        }
    }
    return root;
}

// 打印容器中的所有元素，用于验证测试结果
void printVector(const vector<int>& vec) {
    for (int value : vec) {
        cout << value << " ";
    }
    cout << endl;
}

// 主函数
int main() {

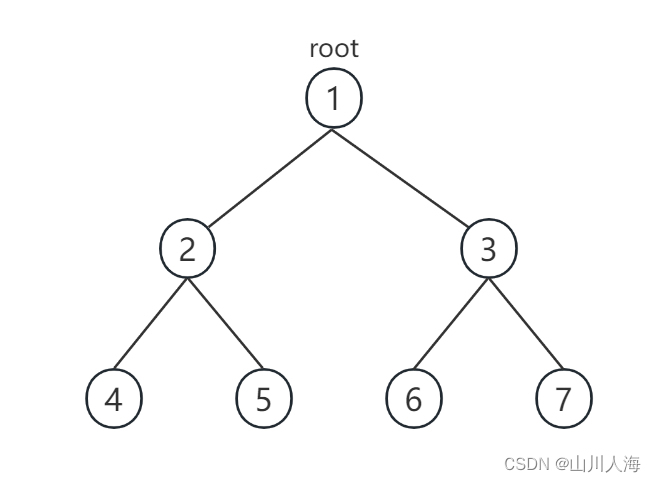
    vector<int> treeValues = { 1, 2, 3, 4, 5, 6, 7 };// 定义二叉树的层序遍历结果，用于构建二叉树
    TreeNode* root = buildTree(treeValues); // 构建二叉树
    Solution1 s1;// 创建Solution类的实例
    Solution2 s2;
    vector<string>result1 = s1.binaryTreePaths(root);// 传入二叉树的根节点
    vector<string>result2 =s2.binaryTreePaths(root);
    cout << "二叉树所有左子叶之和(递归法)是: " <<endl;
    for (auto & s : result1) {
        cout << s << endl;
    }
    cout << endl;
    cout << "二叉树所有左子叶之和(迭代法)是: " <<endl;
    for (auto& s : result1) {
        cout << s << endl;
    }
    cout << endl;
    return 0;
}

三、二叉树所有左子叶之和

1.题目

Leetcode：第 404 题

给定二叉树的根节点 root ，返回所有左叶子之和。

示例 1：

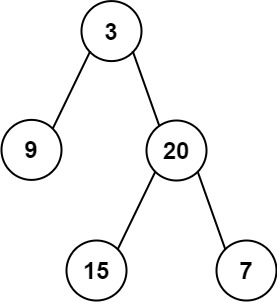
输入: root = [3,9,20,null,null,15,7] 
输出: 24 
解释: 在这个二叉树中，有两个左叶子，分别是 9 和 15，所以返回 24

示例 2:

输入: root = [1]
输出: 0
2.解题思路

使用递归法和迭代法遍历二叉树所有节点，找到所有左子叶并求和。

3.实现代码
#include <iostream>
#include <vector>
#include <stack>
#include <queue>
using namespace std;

// 定义一个结构体TreeNode，用于表示二叉树的节点。
struct TreeNode {
    int val; // 存储节点的值。
    TreeNode* left; // 指向该节点左子树的指针。
    TreeNode* right; // 指向该节点右子树的指针。
    // TreeNode的构造函数，用于创建一个TreeNode实例。
    // 参数x是节点的值，left和right默认为NULL，表示没有左右子节点。
    TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};

// 一、计算二叉树所有左子叶之和（递归法）
class Solution1 {
public:
    // sumOfLeftLeaves函数用于计算二叉树中所有左叶子节点的值的和。
    // 函数接受一个参数：指向二叉树根节点的指针root。
    int sumOfLeftLeaves(TreeNode* root) {
       
        if (root == NULL) return 0; // 如果根节点为空，返回0，因为没有任何叶子节点。

        // 如果根节点的左右子节点都为空，说明根节点是叶子节点，但不是左叶子节点，返回0。
        if (root->left == NULL && root->right == NULL) return 0;

        // 递归地计算左子树中所有左叶子节点的值的和。
        int leftValue = sumOfLeftLeaves(root->left);

        // 检查当前节点的左子节点是否是叶子节点（没有左右子节点）。
        // 如果是，更新leftValue为当前节点左子节点的值。
        if (root->left && !root->left->left && !root->left->right) {
            leftValue = root->left->val;
        }

        int rightValue = sumOfLeftLeaves(root->right);// 递归地计算右子树中所有左叶子节点的值的和。
        int sum = leftValue + rightValue; // 计算左右子树中左叶子节点的值的和。
        return sum;// 返回计算得到的和。
    }
};

// 二、计算二叉树所有左子叶之和（迭代法）
class Solution2 {
public:
    // sumOfLeftLeaves函数用于计算二叉树中所有左叶子节点的值的和。
    // 函数接受一个参数：指向二叉树根节点的指针root。
    int sumOfLeftLeaves(TreeNode* root) {
        stack<TreeNode*> st;// 创建一个栈st，用于在遍历过程中存储节点。
        if (root == NULL) return 0;// 如果根节点为空，直接返回0，因为没有任何叶子节点。
        st.push(root);// 将根节点入栈。
        int result = 0; // 初始化结果变量为0。
        
        while (!st.empty()) {// 使用while循环遍历栈不为空时的所有节点。
            TreeNode* node = st.top(); // 取出栈顶的节点。
            st.pop();// 弹出栈顶的节点。

            // 如果当前节点的左子节点存在，并且左子节点没有左右子节点，即左子节点是叶子节点，
            // 则将左子节点的值加到结果中。
            if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {
                result += node->left->val;
            }

            if (node->left) st.push(node->left); // 如果当前节点有左子节点，将其入栈。
            if (node->right) st.push(node->right);// 如果当前节点有右子节点，将其入栈。
        }
        // 返回计算得到的左叶子节点的值的和。
        return result;
    }
};


//测试
// 辅助函数，用于创建一个新的TreeNode
TreeNode* createNode(int value) {
    return new TreeNode(value);
}

// 辅助函数，用于构建二叉树
TreeNode* buildTree(vector<int>& values) {
    if (values.empty()) return NULL;
    TreeNode* root = createNode(values[0]);
    queue<TreeNode*> queueNode;
    queueNode.push(root);
    int i = 1;
    while (!queueNode.empty()) {
        TreeNode* node = queueNode.front();
        queueNode.pop();
        if (i < values.size()) {
            node->left = createNode(values[i++]);
            queueNode.push(node->left);
        }
        if (i < values.size()) {
            node->right = createNode(values[i++]);
            queueNode.push(node->right);
        }
    }
    return root;
}

// 打印容器中的所有元素，用于验证测试结果
void printVector(const vector<int>& vec) {
    for (int value : vec) {
        cout << value << " ";
    }
    cout << endl;
}

// 主函数
int main() {

    vector<int> treeValues = { 1, 2, 3, 4, 5, 6, 7 };// 定义二叉树的层序遍历结果，用于构建二叉树
    TreeNode* root = buildTree(treeValues); // 构建二叉树
    Solution1 s1;// 创建Solution类的实例
    Solution2 s2;
    int result1 = s1.sumOfLeftLeaves(root);// 传入二叉树的根节点
    int result2 = s2.sumOfLeftLeaves(root);
    cout << "二叉树所有左子叶之和(递归法)是: " << result1 << endl;
    cout << endl;
    cout << "二叉树所有左子叶之和(迭代法)是: " << result2 << endl;
    cout << endl;
    return 0;
}

ps：以上皆是本人在探索算法旅途中的浅薄见解，诚挚地希望得到各位的宝贵意见与悉心指导，若有不足或谬误之处，还请多多指教。 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1583724.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

旋转链表--快慢指针思想

旋转链表--快慢指针思想

相似题型&#xff1a;删除链表的第倒数第n个节点&#xff0c;建议先做&#xff0c;有利于理解 class Solution {public ListNode rotateRight(ListNode head, int k) {ListNode prehead;ListNode firsthead;ListNode secondhead;ListNode lenpre;int length1;if(headnull)retu…
阅读更多...
Linux——fork复制进程

Linux——fork复制进程

1)shell: 在计算机科学中&#xff0c;Shell俗称壳&#xff08;用来区别于核&#xff09;&#xff0c;是指“为使用者提供操作界面”的软件&#xff08;command interpreter&#xff0c;命令解析器&#xff09;。它类似于DOS下的COMMAND.COM和后来的cmd.exe。它接收用户命令&…
阅读更多...
R数据分析：网状meta分析的理解与实操

R数据分析：网状meta分析的理解与实操

meta分析之前有给大家写过&#xff0c;但是meta分析只能比较两个方法。经常是被用来证明在现有研究中显示矛盾结果的干预方法到底有没有效的时候使用&#xff0c;通过证据综合得到某种干预到底有没有用的结论。但是如果我要证明好几种方法到底哪个最优&#xff0c;这个时候meta…
阅读更多...
谈谈功率IC巨头—士兰微

谈谈功率IC巨头—士兰微

大家好&#xff0c;我是砖一。 今天给大家分享一下士兰微电子公司&#xff0c;&#xff0c;有做功率元器件&开关电源和IC的朋友可以了解一下&#xff0c;希望对你有用~ 1 公司介绍 士兰微电子成立于1997年&#xff0c;于2003年上市&#xff0c;总部位于杭州&#xff0c;…
阅读更多...
智能面试——录音及播放下载js-audio-recorder — post请求，formdata传参

智能面试——录音及播放下载js-audio-recorder — post请求，formdata传参

录音插件 js-audio-recorder bug&#xff1a;本地调试调取不起来麦克风 浏览器配置安全域名 chrome://flags/Insecure origins treated as secure输入域名即可电脑需要连接上耳机 <template><div class"BaseRecorder"><div class"BaseRecorder-r…
阅读更多...
seo调优

seo调优

SEO 网站地图&#xff1a;sitemap.xmlrobots.txtxxx.com/www.xxx.com 解析到服务器&#xff0c;xxx.com 301 到 www.xxx.comhttps百度站点管理标题描述关键词标签语义化内链外链死链链接html结尾友情链接前端架构 注意&#xff1a;已收录链接&#xff0c;禁止改变链接地址 ro…
阅读更多...
【C++第三阶段】deque容器评委打分案例

【C++第三阶段】deque容器评委打分案例

以下内容仅为当前认识&#xff0c;可能有不足之处&#xff0c;欢迎讨论&#xff01; 文章目录 构造函数赋值操作大小操作插入删除数据存取排序评委评分案例描述 deque容器 双端数组&#xff0c;可以对头端插入删除操作。 如下图所示。 头部有插入删除操作&#xff0c;尾部亦然…
阅读更多...
国内如何实现GPT升级付款

国内如何实现GPT升级付款

本来想找国外的朋友代付的&#xff0c;但是他告诉我他的信用卡已经被绑定了他也升级了所以只能自己想办法了。就在一位博主下边发现了这个方法真的可以。只是需要与支付宝验证信息。刚开始不敢付款害怕被骗哈哈&#xff0c;我反诈骗意识绝对杠杠的 该方法就是我们办理一张虚拟…
阅读更多...
After Effects 2024 中文激活版 高效工作流程与创新的视觉特效 mac/win

After Effects 2024 中文激活版 高效工作流程与创新的视觉特效 mac/win

After Effects 2024是Adobe公司推出的一款专业视频特效制作软件&#xff0c;广泛应用于电影、电视、动画等媒体制作领域。它凭借强大的功能和灵活的操作&#xff0c;帮助用户轻松创建电影级影片字幕、片头和过渡效果&#xff0c;以及实现立体效果和动态场景的切换。 同时&#…
阅读更多...
Java-接口—知识（基础）

Java-接口—知识（基础）

承接上一节&#xff0c;我们讨论了抽象类和抽象方法。 那我们尝试在抽象的道路上走的更远一点&#xff0c;先来总结一下抽象&#xff1b; 抽象类&#xff1a;类中的属性规范了子类必须有什么样的特征&#xff0c;有什么状态。类中的方法规范了子类必须有什么行为&#xff0c;…
阅读更多...
【Spring Security】2.实现最简单的身份验证

【Spring Security】2.实现最简单的身份验证

文章目录 一、找到官网的身份认证&#xff08;authentication&#xff09;示例代码二、实现最简单的身份验证1、创建Spring Boot项目2、创建IndexController3、创建index.html4、启动项目测试Controller 三、{/logout}的作用四、页面样式无法加载的问题 一、找到官网的身份认证…
阅读更多...
文本处理常见命令

文本处理常见命令

目录 前言-了解Linux目录结构 一、cat-查看文件内容 1.表现形式 2.常用选项 3.示例 二、more-查看文件内容 1.表现形式 2.交互操作方法 3.示例 三、less-查看文件内容 1.表现形式 2.交互操作方法 四、head-从头查看文件内容 五、tail-从尾查看文件内容 六、wc-统…
阅读更多...
设计模式学习笔记 - 设计模式与范式 -行为型：10.迭代器模式（中）：遍历集合时，为什么不能增删集合？

设计模式学习笔记 - 设计模式与范式 -行为型：10.迭代器模式（中）：遍历集合时，为什么不能增删集合？

概述 上篇文章&#xff0c;我们通过给 ArrayList 和 LinkedList 容器实现迭代器&#xff0c;学习了迭代器模式的原理、实现和设计意图。迭代器模式主要主要是解耦容器代码和遍历代码。 本章&#xff0c;我们来深挖一下&#xff0c;如果在使用迭代器遍历集合的同时增加、删除集…
阅读更多...
1999-2022年各省研究与试验发展人员全时当量数据/省研发人员全时当量数据/(RD)人员全时当量（无缺失）

1999-2022年各省研究与试验发展人员全时当量数据/省研发人员全时当量数据/(RD)人员全时当量（无缺失）

1999-2022年各省研究与试验发展人员全时当量数据/省研发人员全时当量数据/(R&D)人员全时当量&#xff08;无缺失&#xff09; 1、时间&#xff1a;1999-2022年 2、来源&#xff1a;科技年鉴 3、指标&#xff1a;研究与试验发展人员全时当量/研发人员全时当量 4、范围&a…
阅读更多...
代码随想录算法训练营Day50|LC123 买卖股票的最佳时机IIILC188 买卖股票的最佳时机IV

代码随想录算法训练营Day50|LC123 买卖股票的最佳时机IIILC188 买卖股票的最佳时机IV

一句话总结&#xff1a;虽然是困难题&#xff0c;其实都只需要对122 买卖股票的最佳时机II稍作变形即可。 原题链接&#xff1a;123 买卖股票的最佳时机III 相较于买卖股票的最佳时机和股票II来说&#xff0c;本题加了最多操作两次的限制。那么这里实际上就可以直接用滚动数组…
阅读更多...
用C代码实现环形缓冲区（ring buf）

用C代码实现环形缓冲区（ring buf）

用C代码实现环形缓冲区&#xff08;ring buf&#xff09; 概述环境介绍launch.json(没改&#xff09;tasks.json注意 代码ringbuf.cringbuf.hmain.c 测试说明工程代码下载 概述 因嵌入式项目需要&#xff0c;串口接收的数据有很高的周期性发送频率&#xff0c;原方式通过查询接…
阅读更多...
小程序项目思路分享爬虫

小程序项目思路分享爬虫

小程序项目思路分享爬虫 具体需求&#xff1a; 有这几个就行&#xff0c;门店名称门店地址门店类型&#xff0c;再加上省、市、县/区门店名称&#xff1a;storeName 门店地址&#xff1a;storeAddress 程序运行&#xff1a; honor_spider获取经纬度信息。 经纬度——>详…
阅读更多...
Mybatis plus 使用通用枚举

Mybatis plus 使用通用枚举

说明&#xff1a;mybatis plus 使用枚举可实现数据库存入时指定值保存&#xff0c; 读取时指定值展示&#xff08;返给前端&#xff09; 可通过继承IEnum<T>、 EnumValue实现 1、引包 <dependency><groupId>mysql</groupId><artifactId>mysql-…
阅读更多...
esxi上给centos7虚拟机扩容硬盘

esxi上给centos7虚拟机扩容硬盘

原来centos7硬盘分配的空间只有40GB 需要直接扩容到200GB 扩容前 扩容后 扩容步骤&#xff1a; 1 .在esxi平台上关机虚拟机&#xff0c;将硬盘调整为200GB&#xff0c;然后开机 2.请出chatGPT 1. 创建新分区 使用剩余的磁盘空间创建一个新的分区。你可以使用fdisk&#xf…
阅读更多...
归档数据shell脚本

归档数据shell脚本

系统中数据很重要&#xff0c;为确保数据不会丢失&#xff0c;定时备份数据是一个必要的习惯。制定一个存储重要文件的数据备份计划也绝非易事&#xff0c;而shell脚本可以祝我们一臂之力。 1.创建需要备份配置文件的路径文件。(BACKUP_FILE) 2.以日期为备份文件的后缀。 3.判断…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023