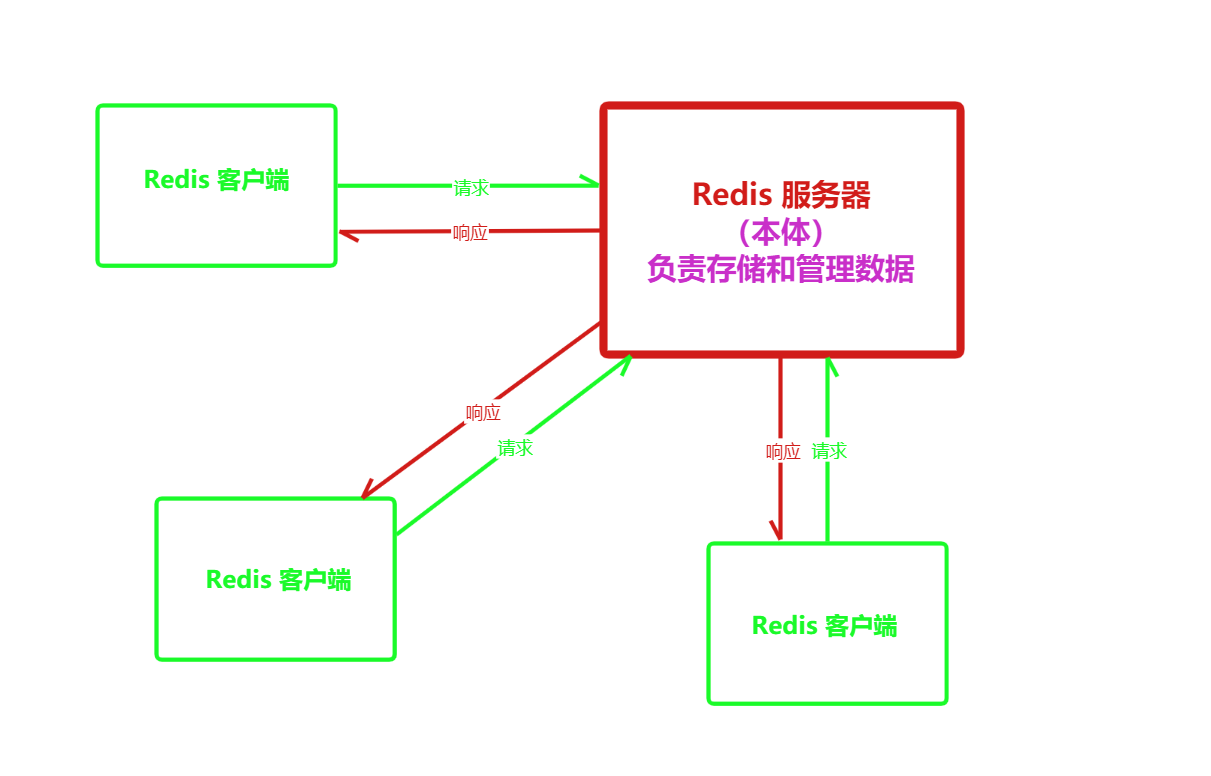
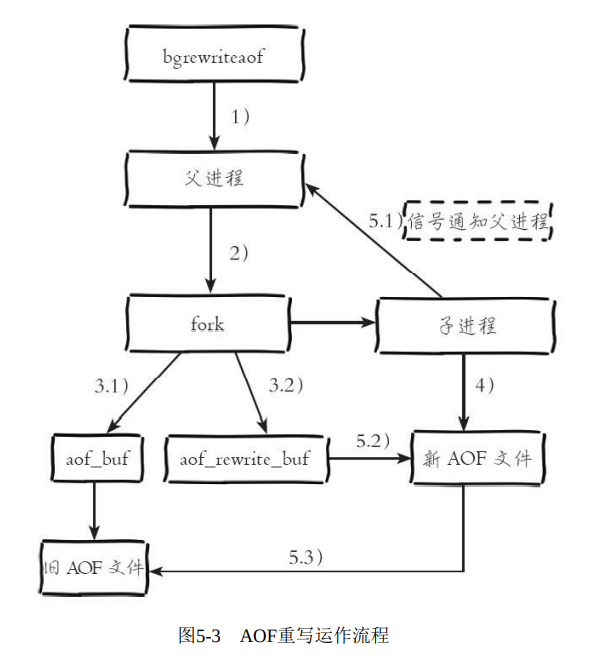
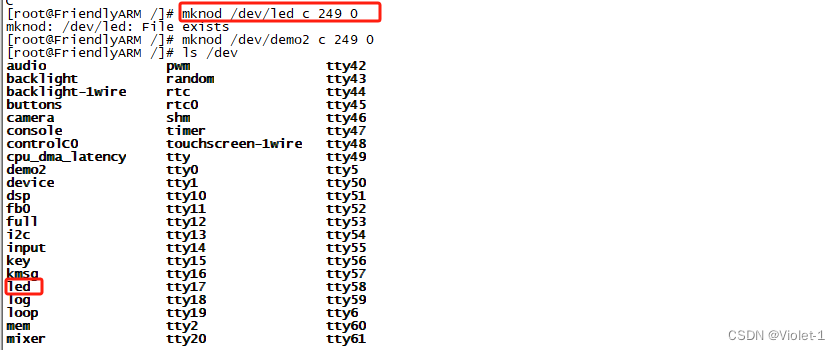
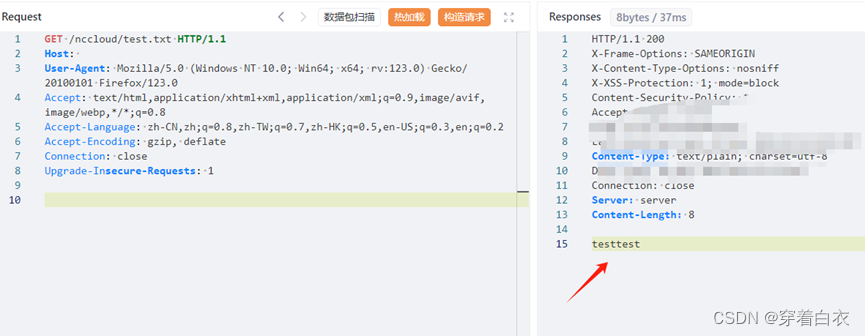
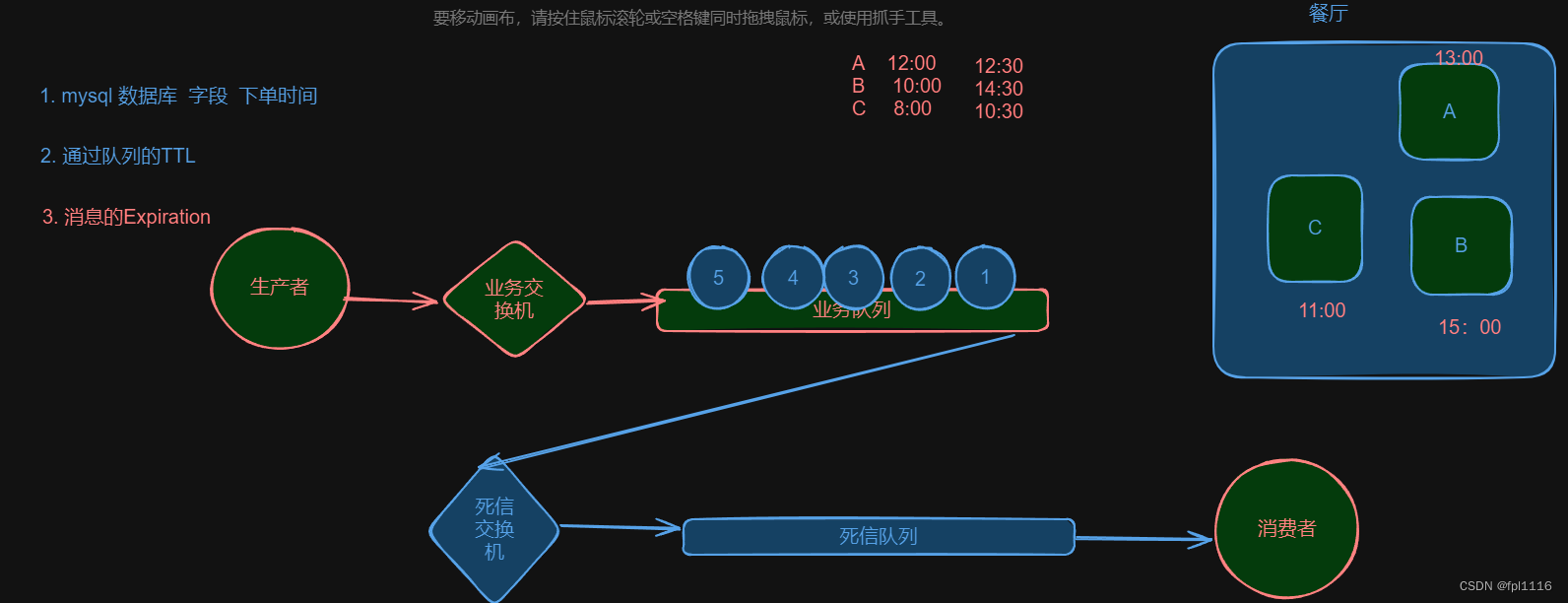
原理图：


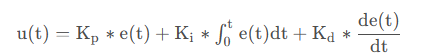
（1）位置式PID
是1：当前系统的实际位置，与你想要达到的预期位置的偏差， 2：进行PID控制,误差会一直累加，会使当前输出与过去的所有输入相关，输入uk出错，会导致系统大幅波动 3：位置式PID在积分项达到饱和时,误差仍然会在积分作用下继续累积，一旦误差开始反向变化，系统需要一定时间从饱和区退出，所以在u(k)达到最大和最小时，要停止积分作用，并且要有积分限幅和输出限幅， 4：用位置式PID时，一般我们直接使用PD控制，不使用积分项

实际应用中，用差分代替微分，连加代替积分，也就是离散型PID
令：

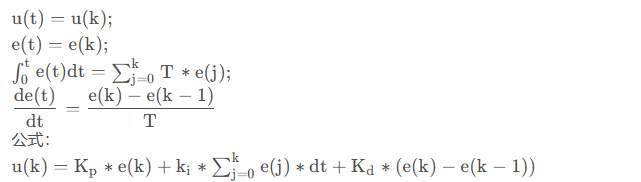
(1)实现：位置模式PID

#include <math.h>
#include <stdio.h>
#include <iostream>
#include <string>
#include "matplotlibcpp.h"
#include <vector>
#include <math.h>
#include <string>
#include<stdlib.h>
namespace plt = matplotlibcpp;


class pid_p
{
private:
    float ki;
    float kp;
    float kd;
    float ek;
    float ek_1;
    float actual;
    float de;
    float target;
    float yk;
public:
    pid_p();
    ~pid_p();
    pid_p(float p,float i,float d);
    void get_error();
    
    void get_value(float act,float tar);
    float update();
};

pid_p::pid_p():kp(0),ki(0),kd(0),ek(0),ek_1(0),de(0),actual(0),yk(0)
{
}
pid_p::pid_p(float p,float i,float d):ek(0),ek_1(0),de(0),actual(0),yk(0)
{
    kp=p;
    ki=i;
    kd=d;
}

pid_p::~pid_p()
{
}
void pid_p::get_value(float act,float tar)
{
    actual=act;
    target=tar;
    get_error();
    printf("actual:%f,target%f",actual,target);
}
void pid_p::get_error()
{
    ek=target-actual;
}
float pid_p::update()
{
    de+=ek;
    yk=kp*ek+ki*de+kd*(ek-ek_1);
    printf("p:%f,i:%f,d:%f,act:%f,yk:%f,ek:%f\r\n",kp,ki,kd,actual,yk,ek);
    ek_1=ek;
    return yk;

}

//输入三个参数kp,ki,kd
int main(int argc,char ** argv)
{   float target=1000;
    std::string str_p=argv[1];
    std::string str_i=argv[2];
    std::string str_d=argv[3];
    // std::string str_p="0.35";
    // std::string str_i="0.0001";
    // std::string str_d="0.0001";
    float act=0;int N=100;
   
    float kp=atof(str_p.c_str());
    float ki=atof(str_i.c_str());
    float kd=atof(str_d.c_str());
    
    pid_p a(kp,ki,kd);
    std::vector<float> x,y;
    for (int i=0;i<N;i++)
    {
        x.push_back(i);
        y.push_back(act);
        a.get_value(act,target);
        act+=a.update();
        a.pid_printf();
        //if(act>target)break;
    }
    plt::plot(x,y);
    plt::show();
}

（2）增量式PID
原理：使控制器输出为增量，尽量使每次数据均与过去数据无关，没有积分项。
公式：

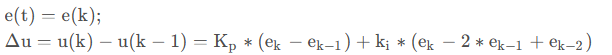
实现

class pid_add
{
    private:
        float kp,ki,kd,ek,ek_1,ek_2,uk,yk,delta_u;
    public:
        pid_add();
        pid_add(float p,float i,float d);
        void get_value(float act,float tar);
        void update_error();
        float update();

};
pid_add::pid_add():kp(0),ki(0),kd(0),uk(0),ek(0),ek_1(0),yk(0)
{

};

pid_add::pid_add(float p,float i,float d):uk(0),ek(0),ek_1(0),yk(0)
{
    kp=p;
    ki=i;
    kd=d;
};

void pid_add::get_value(float act,float tar)
{
    uk=act;
    yk=tar;
}
void pid_add::update_error()
{
    ek_1=ek;
    ek=yk-uk;
}

float pid_add::update()
{
    update_error();
    delta_u=kp*(ek-ek_1)+ki*ek+kd*(ek-2*ek_1+ek_2);
    return delta_u;
}

(3) 积分分离式PID

原理：在系统误差较大时，取消积分环节；当误差较小时，引入积分环节。这样既不影响控制器的动态性能，又可以提高控制器的稳态精
实现：在位置式/增量式PID加入积分环节一个阈值，实现略

(4) 抗饱和积分式PID
原理：在计算U(k)的时候，先判断上一时刻的控制量U(k-1)是否已经超出了限制范围。若U(k-1)>Umax，则只累加负偏差；若U(k-1)<Umin，则只累加正偏差。从而避免控制量长时间停留在饱和区。
实现：

class pid_antisaturation
{
    private:
        float kp,ki,kd,uk,uk_1,yk,ek,ek_1,ek_2;
        const float max_uk_1=500,min_uk_1=-500;
    public:
        pid_antisaturation():kp(0),ki(0),kd(0),uk(0),yk(0),ek(0),ek_1(0),ek_2(0),uk_1(0)
        {};
        pid_antisaturation(float p,float i,float d):kp(p),ki(i),kd(d),uk(0),yk(0),ek(0),ek_1(0),ek_2(0),uk_1(0)
        {};
        void get_value(float act,float target);
        void update_error();
        float update();
};
void pid_antisaturation::get_value(float act,float target)
{
    uk_1=uk;
    uk=act;
    yk=target;
}
void pid_antisaturation::update_error()
{
    ek_2=ek_1;
    ek_1=ek;
    ek=yk-uk;
}
float pid_antisaturation::update()
{
    float increase;
    update_error();
    if((uk_1>max_uk_1)&(ek>0))
    {
        ek=0;
    }
    if((uk_1<min_uk_1)&(ek<0))
    {
        ek=0;
    }
    increase=kp*(ek-ek_1)+ki*ek+kd*(ek-2*ek_1+ek_2);
    printf("p:%f,i:%f,d:%f,act:%f,yk:%f,ek:%f\r\n",kp,ki,kd,uk,yk,ek);
    return increase;
}