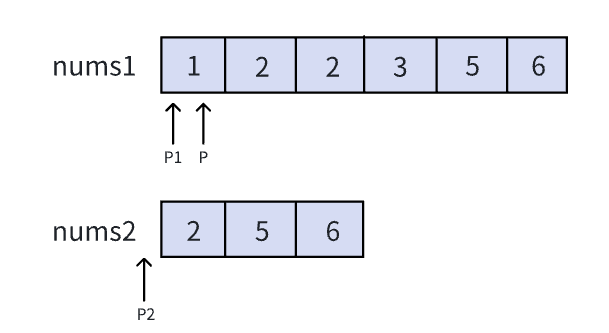
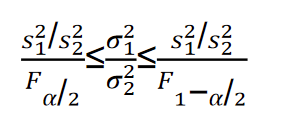我们在前面说了一下参数估计中的点估计，接下来，我们来讲一下区间估计。

区间估计——在点估计的基础上，给出总体参数估计的一个估计区间，该区间由样本统计量加减估计误差而得到。

• 置信水平——如果将构造置信区间的步骤重复多次，置信区间中包含总体参数真值的次数所占的比例称为置信水平，也称为置信度或置信系数（confidence coefficient）。常用的置信水平有90%、95%和99%。

  如果用某种方法构造的所有区间中有95%的区间包含总体参数的真值，5%的区间不包含总体参数的真值，那么，用该方法构造的区间称为置信水平为95%的置信区间。
  也就是说，我现在有100个总体，现在随机抽取20个作为样本，那么这样的样本就会有很多个。假设有100个样本，那么就对应100个置信区间，在这100个置信区间里面，有95个区间包含总体参数的真值，就说明这是置信水平为95%的置信区间。**所以说，置信水平是所构造的区间中包含真值的比例，而不是所构造的某个区间包含真值的概率。**一个特定区间总是“包含”或“绝对不包含”参数的真值，不存在“以多大的概率包含总体参数”的问题。例如，区间为【60,70】，那么80就没在这个区间内，不存在“80以90%的概率在【60,70】内”的这样的说法。

  如上图所示，我们依据不同的样本构造了20个置信区间。在这些区间中，有些包含了总体参数真值$\mu$，有些就没有包含。
  实际估计时往往只抽取一个样本，此时所构造的是与该样本相联系的一定置信水平(比如95%)下的置信区间。我们希望这个区间是大量包含总体参数真值的区间中的一个，但它也可能是少数几个不包含参数真值的区间中的一个。

若我们按照99%的置信水平构造置信区间，也就是说，所构造的区间中包含真值的比例为99%，说明包含真值的区间很多，那我们随机抽取一个，就会觉得抽中包含真值的区间的概率很大。

对于区间估计而言，我们只考虑$\mu$和${\sigma }^2$区间估计，例如两个正态总体就是考虑${\mu }_1-{\mu }_2$和${\sigma }_1^2/{\sigma }_2^2$的区间估计，这是因为我们只知道${\mu }_1-{\mu }_2$和${\sigma }_1^2/{\sigma }_2^2$分布函数(分布函数说白了就是规律分布，没有规律就无法进行预测)，而我们没办法知道${\mu }_1/{\mu }_2$和${\sigma }_1^2-{\sigma }_2^2$分布函数，所以就不能对这两个进行参数估计。

1.一个总体参数的区间估计

1.1 总体均值的区间估计

1.1.1 正态总体,方差已知,或非正态总体,大样本

  当总体服从正态分布且${\sigma }^2$已知时,或者总体不是正态分布但为大样本时,样本均值$\overline{x}$的抽样分布均为正态分布,其数学期望为总体均值$\mu$,方差为${\sigma }^2/n$。而样本均值经过标准化以后的随机变量服从标准正态分布,即

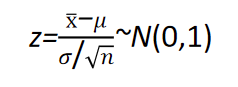
  总体均值$\mu$在$1-\alpha$置信水平下的置信区间为

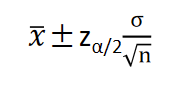
• 如果总体服从正态分布但${\sigma }^2$未知,或总体并不服从正态分布,只要是在大样本条件下,上式中的总体方差${\sigma }^2$就可以用样本方差$s^2$代替,这时总体均值$\mu$在$1-\alpha$置信水平下的置信区间可以写为:
  

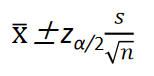
1.1.2 正态总体,方差未知,小样本

  如果总体方差${\sigma }^2$未知,而且是在小样本情况下,则需要用样本方差$s^2$代替${\sigma }^2$,这时,样本均值经过标准化以后的随机变量服从自由度为$(n-1)$的$t$分布,即

  根据$t$分布建立的总体均值$\mu$在$1-\alpha$置信水平下的置信区间为:

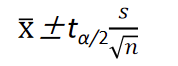
1.1.3 一个总体均值的区间估计小结

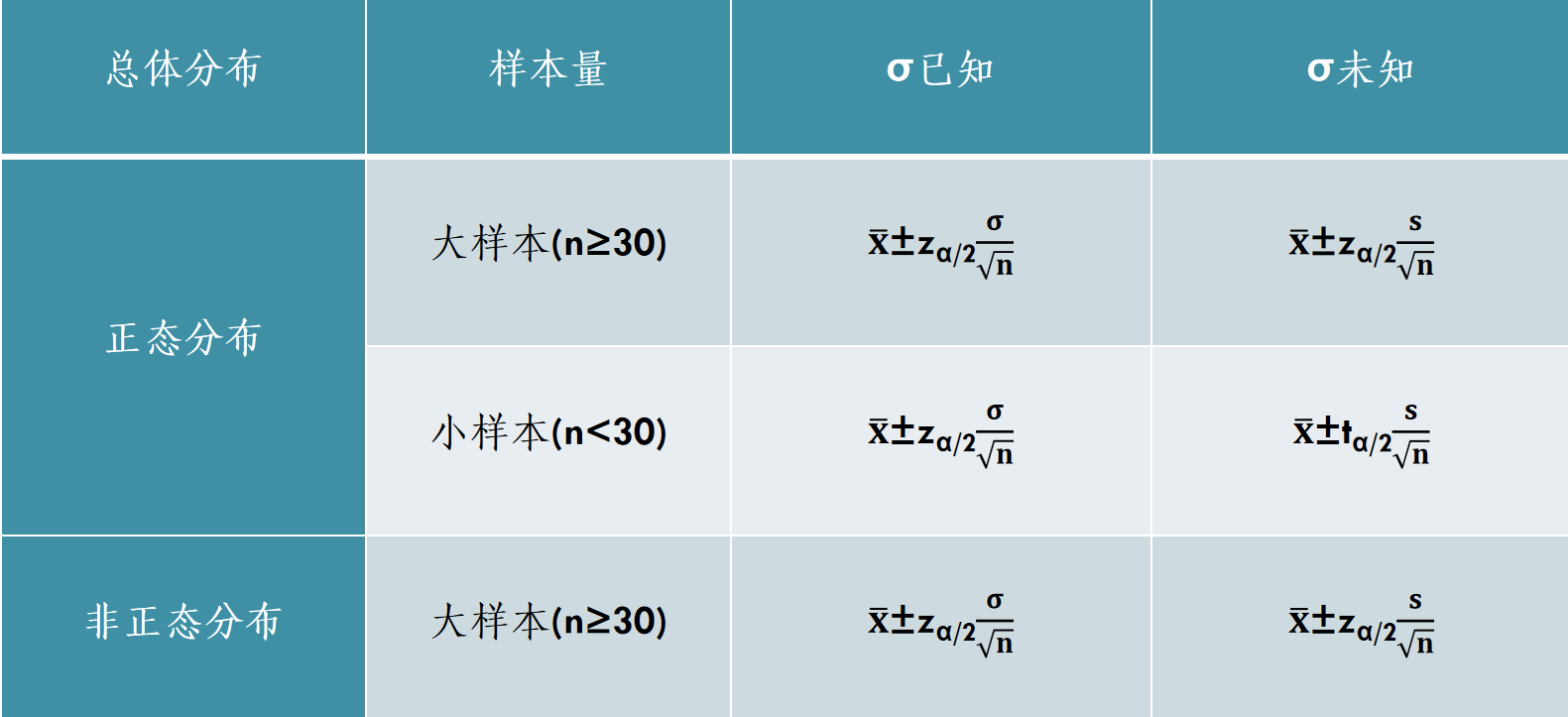
总而言之，如果总体参数已知，那么我们就用总体参数的真实值，毕竟是要估计总体参数。若未知，则用样本来代替。常用的是样本均值代替总体均值，样本方差代替总体方差。

1.2 总体比例的区间估计

  当样本量足够大时,比例$p$的抽样分布可用正态分布近似。$p$的数学期望为$E(p)=\pi$;p的方差为${\sigma }_{\mathfrak{p}}^2=\frac{\pi \left(1-\pi \right)}{\mathfrak{n}}$。样本比例经标准化后的随机变量服从标准正态分布,即

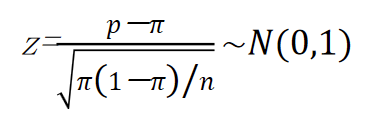
  在样本比例$p$的基础上加减估计误差$Z_{\alpha /2}{\sigma }_p$,即得总体比例$\pi$在$1-\alpha$置信水平下的置信区间为:

  用样本比例$p$来代替$\pi$时,总体比例的置信区间可表示为:

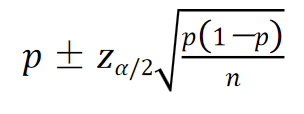
1.3 总体方差的区间估计

  建立总体方差${\sigma }^2$的置信区间,也就是要找到一个$\chi 2$值,使其满足

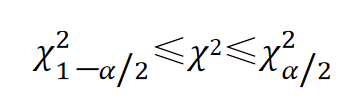
  由于$\frac{(n-1)s^2}{{\sigma }^2}\sim {\chi }^2(n-1)$，可用它来代替$\chi 2$,于是有

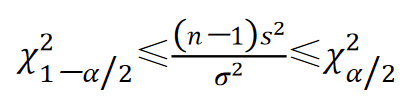
  根据上式可推导出总体方差${\sigma }^2$在$1-\alpha$置信水平下的置信区间为:

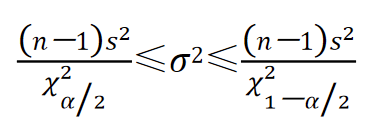
2.两个总体参数的区间估计

1.1 两个总体均值之差的区间估计-独立大样本

独立样本(independent sample)——如果两个样本是从两个总体中独立抽取的,即一个样本中的元素与另一个样本中的元素相互独立

  如果两个总体都为正态分布,或两个总体不服从正态分布但两个样本都为大样本$(n_1\ge 30和n_2\ge 30)$,根据抽样分布的知识可知,两个样本均值之差KaTeX parse error: Expected 'EOF', got '̅' at position 3: x ̲̅_1-x ̅_2的抽样分布服从期望值为$({\mu }_1-{\mu }_2)$、方差为$({\sigma }_1^2/n_1+{\sigma }_2^2/n_2)$的正态分布,两个样本均值之差经标准化后服从标准正态分布,即

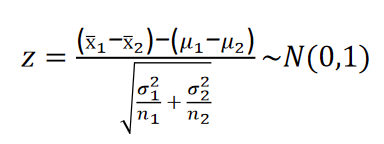
  当两个总体的方差${\sigma }_1^2$和${\sigma }_2^2$都已知时,两个总体均值之差${\mu }_1-{\mu }_2$在$1-\alpha$置信水平下的置信区间为:

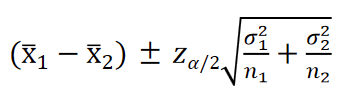
  当两个总体的方差${\sigma }_1^2$和${\sigma }_2^2$未知时,可用两个样本方差$s_1^2$和$s_2^2$来代替,这时,两个总体均值之差${\mu }_1-{\mu }_2$在$1-\alpha$置信水平下的置信区间为:

1.2 两个总体均值之差的区间估计-独立小样本

• 方差${\sigma }_1^2$和${\sigma }_2^2$未知但相等
    当两个总体的方差${\sigma }_1^2$和${\sigma }_2^2$未知但相等时,即${\sigma }_1^2={\sigma }_2^2$,需要用两个样本的方差$s_1^2$和$s_2^2$来估计,这时,需要将两个样本的数据组合在一起,以给出总体方差的合并估计量$s_p^2$,计算公式为:
  
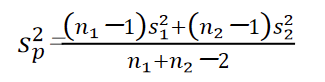
    这时,两个样本均值之差经标准化后服从自由度为$(n1+n2-2)$的$t$分布,即

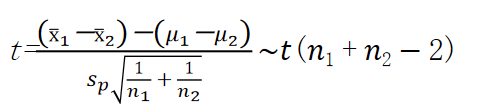
  因此,两个总体均值之差${\mu }_1-{\mu }_2$在$1-\alpha$置信水平下的置信区间为:

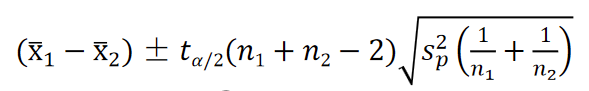
• 方差${\sigma }_1^2$和${\sigma }_2^2$未知且不相等
    当两个总体的方差${\sigma }_1^2$和${\sigma }_2^2$未知但相等时,即${\sigma }_1^2={\sigma }_2^2$,需要用两个样本的方差$s_1^2$和$s_2^2$来估计,这时,需要将两个样本的数据组合在一起,以给出总体方差的合并估计量$s_p^2$,计算公式为:
    两个样本均值之差经标准化后近似服从自由度为$v$的$t$分布,自由度$v$的计算公式为:

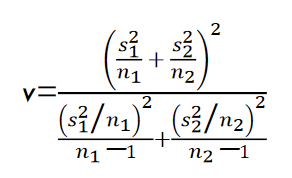
  两个总体均值之差在$1-\alpha$置信水平下的置信区间为:

1.3 两个总体均值之差的区间估计——匹配样本

匹配样本，就是两个样本有关系，不独立。例如：A班期中和期末成绩，这就是一个匹配样本，存在一一对应的关系；而A班期中和B班期中则就是独立样本。

  在大样本情况下，两个总体均值之差${\mu }_d={\mu }_1-{\mu }_2$在$1-\alpha$置信水平下的置信区间为:

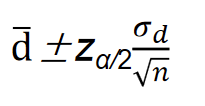
  式中,$d$表示两个匹配样本对应数据的差值;KaTeX parse error: Expected 'EOF', got '̅' at position 3: d ̲̅表示各差值的均值;${\sigma }_d$表示各差值的标准差。当总体的${\sigma }_d$未知时,可用样本差值的标准差$s_d$来代替。
  在小样本情况下,假定两个总体各观察值的配对差服从正态分布。两个总体均值之差${\mu }_d={\mu }_1-{\mu }_2$在$1-\alpha$置信水平下的置信区间为:

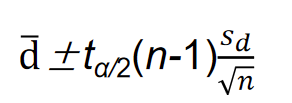
1.3 两个总体比例之差的区间估计

  由样本比例的抽样分布可知,从两个二项总体中抽出两个独立的样本,则两个样本比例之差的抽样分布服从正态分布。同样,两个样本的比例之差经标准化后服从标准正态分布,即

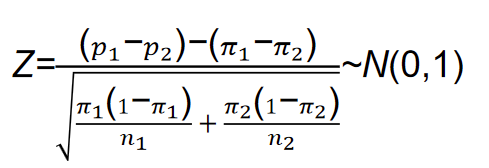
  两个总体比例${\pi }_1$和${\pi }_2$未知时,可用样本比例$p_1$和$p_2$来代替，根据正态分布
建立的两个总体比例之差${\pi }_1-{\pi }_2$在$1-\alpha$置信水平下的置信区间为:

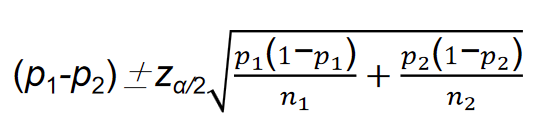
1.3 两个总体方差比的区间估计

  建立两个总体方差比的置信区间,也就是要找到一个$F$值,使其满足

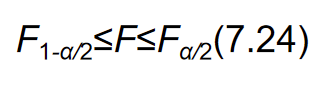
  由于$\frac{s_1^2}{s_2^2}\cdot \frac{{\sigma }_2^2}{{\sigma }_1^2}\sim F(n_1-1,n_2-1)$,故可用它来代替$F$,于是有

  由此可以推导出两个总体方差比${\sigma }_1^2/{\sigma }_2^2$在$1-\alpha$置信水平下的置信区间为: