最长公共子序列（线性dp）-java

news2024/11/24 23:06:19

本文主要来描述两个字符串的最长公共子序列问题

文章目录

前言

一、最长公共子序列

二、算法思路

1.dp[i][j]的四种情况

2. dp[i-1][j]、dp[i][j-1]、dp[i-1][j-1]的关系

3.dp数组的状态转移方程

4.dp数组具体如下

三、代码如下

1.代码如下（示例）：

2.读入数据

3.代码运行结果

总结

前言

本文主要来描述两个字符串的最长公共子序列问题

提示：以下是本篇文章正文内容，下面案例可供参考

一、最长公共子序列

定两个长度分别为 N 和 M 的字符串 A 和 B，求既是 A 的子序列又是 B的子序列的字符串长度最长是多少。

二、算法思路

1.dp[i][j]的四种情况

引入字符数组a和b，字符数组a存入字符串A，字符数组b存入字符串B。

我们引入二维数组dp，dp[i][j]表示的含义为表示所有在第一个字符串中出现的前i个字母即a[i]和第二个字符串中出现的前j个字母即b[j]的公共子序列。

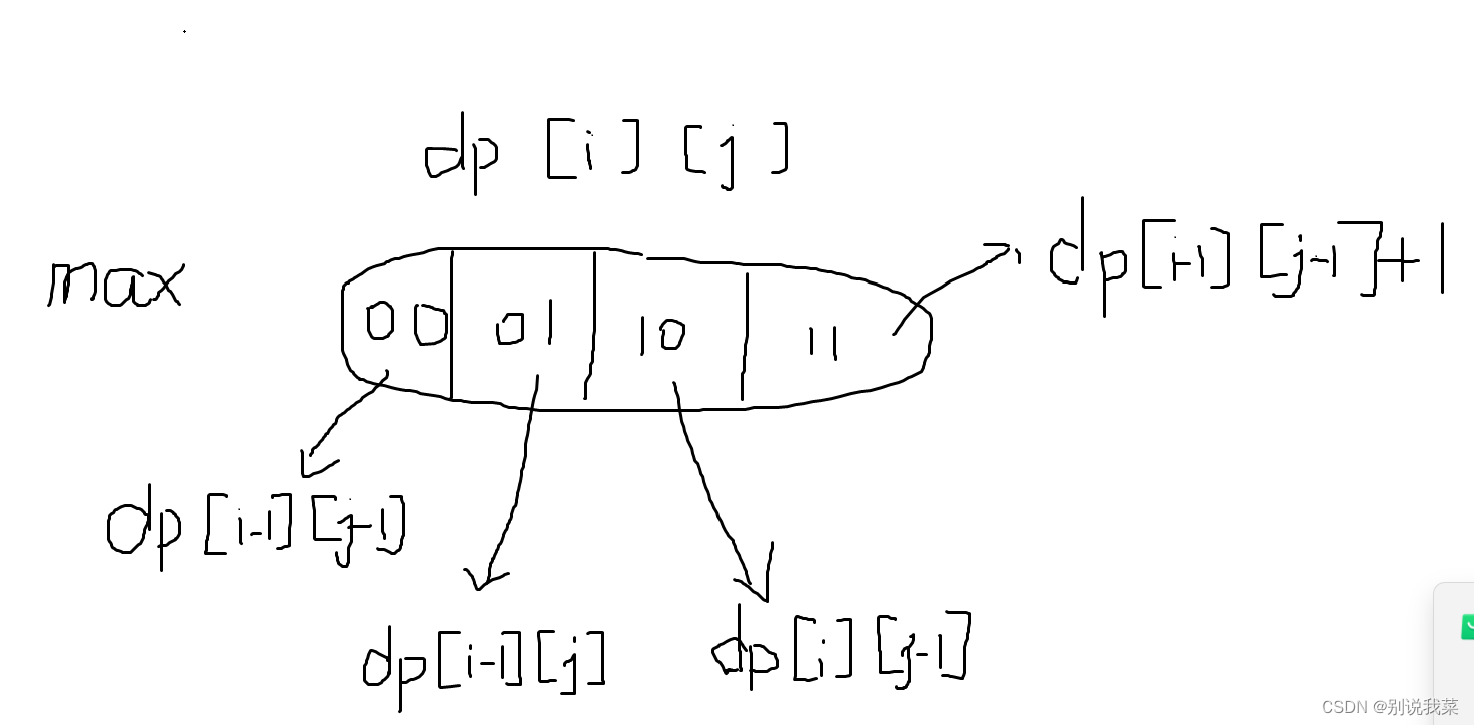
图1.1思路模拟

dp[i][j]通常是由以下4种情况构成

当a[i]和b[j]都不取。即取字符串A前i -1个字符和字符串B的前j-1个字符的最长公共子序列的长度dp[i-1]dp[j-1]
当a[i]不取，b[j]取。而dp[i-1][j]表示的是字符串A的前i-1个字符和字符串B的前j个字符的最长公共子序列，其中可能包括字符串B的第j个字符也可能不包括字符串B的第j个字符。
当a[i]取，b[j]不取。dp[i][j-1]表示的字符串A的前i个字符和字符串B的前j-1的字符的最长公共子序列，其中可能包括字符串A的第i个字符也可能不包括字符串A的第i个字符。
当a[i]和b[j]都取，即字符串A的第i个字符和字符串B的第j个字符相等时，那么就代表我们取字符串A的前i-1个字符和字符串B的前j-1个字符的最长公共子序列的长度（即dp[i-1][j-1]）加上1，既可以得到此时dp[i][j]的值，即 $dp[i][j] = dp[i-1]dp[j-1]+1$ 。

2. dp[i-1][j]、dp[i][j-1]、dp[i-1][j-1]的关系

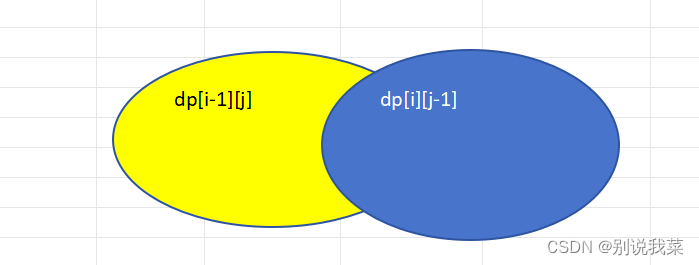
图2.1dp[i-1][j]、dp[i][j-1]和dp[i-1][j-1]的关系

dp[i-1][j]表示字符串A的前i-1个字符和字符串B的前j个字符的最长公共子序列。

dp[i][j-1]表示的字符串A的前i个字符和字符串B的前j-1的字符的最长公共子序列

那么dp[i-1][j]和dp[i][j-1]的重复的部分就表示字符串A的前i-1个字符和字符串B的前j-1个字符串的最长公共子序列即dp[i-1][j-1]。（不取字符串A的第i个字符和字符串B的第j个字符）

3.dp数组的状态转移方程

因为我们dp[i][j]表示的值是上述所描述的4种情况取最大值，那么我们就不必再取dp[i-1][j-1]的值，因为dp[i-1][j]的值和dp[i][j-1]的值肯定都比dp[i-1][j-1]的值大，dp[i-1][j-1]分别是dp[i-1][j]和dp[i][j-1]的子集。

当a[i] != b[j]时:

$dp[i][j] = max(dp[i-1][j],dp[i][j-1])$

当a[i] = b[j]时：

$dp[i][j] =max(dp[i][j], dp[i-1][j-1]+1)$

4.dp数组具体如下

我们以测试样例字符串acbd和字符串abedc为例，dp数组各个值如下：

0 0 0 0 0 0 
0 1 1 1 1 1 
0 1 1 1 1 2 
0 1 2 2 2 2 
0 1 2 2 3 3

三、代码如下

1.代码如下（示例）：


import java.io.*;
import java.util.Scanner;

public class 最长公共子序列 {
    static PrintWriter pw = new PrintWriter(new OutputStreamWriter(System.out));
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer st = new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static void main(String[] args) throws Exception{
        Scanner sc =new Scanner(new BufferedReader(new InputStreamReader(System.in)));
        int n = sc.nextInt();
        int m = sc.nextInt();
        String a = sc.next();
        String b = sc.next();
        char[] Achar = new char[1010];
        char[] Bchar = new char[1010];
        for(int i = 1;i <= n;i++){
            Achar[i] = a.charAt(i-1);
        }
        for(int i = 1;i <= m;i++){
            Bchar[i] = b.charAt(i-1);
        }
        int[][] dp = new int[1010][1010];
        for(int i = 1;i <= n;i++){
            for(int j = 1; j<= m;j++){
                dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);
                if(Achar[i] == Bchar[j]){
                    dp[i][j] = Math.max(dp[i][j],dp[i-1][j-1]+1);
                }
            }
        }
        pw.println(dp[n][m]);
        pw.flush();
    }
    public static int nextInt()throws Exception{
        st.nextToken();
        return (int)st.nval;
    }
}