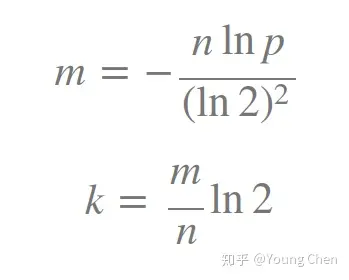C++位图和布隆过滤器（含哈希切割）

news2024/10/7 6:44:11

文章目录

  • C++位图和布隆过滤器（含哈希切割）
    • 1、位图（Bitmap）
      • 1.1、位图的概念
      • 1.2、位图的使用
      • 1.3、位图的模拟实现
      • 1.4、位图相关面试题
    • 2、布隆过滤器（Bloom Filter）
      • 2.1、布隆过滤器的概念
      • 2.2、布隆过滤器的插入
      • 2.3、布隆过滤器的模拟实现
      • 2.4、布隆过滤器相关面试题
    • 3、哈希切分（哈希切割）
    • 4、海量数据处理

img

C++位图和布隆过滤器（含哈希切割）

位图和布隆过滤器都是哈希思想的应用

1、位图（Bitmap）

1.1、位图的概念

位图是一种用于表示集合的数据结构，它通常用一个比特位序列来表示一组元素的存在与否。在 C++ 中，位图通常使用一个二进制数组来实现。每个元素对应位图中的一个比特位，如果该元素存在于集合中，则对应的比特位被设置为1，否则为0。

应用场景：存储大量的布尔值信息，节省内存空间。还可以快速判断一个元素是否存在于集合中，时间复杂度为 O(1)。

优点：空间效率高，占用内存少。查询效率高，时间复杂度低。

缺点：不能存储重复元素（使用两个及以上的位图可以解决）。对于范围较大的数据，可能会占用较多的内存空间。

1.2、位图的使用

void test_bs1() {
    bitset<1000> bs;
    int a[] = {1, 5, 7, 8, 999, 44, 22, 44, 0, 3, 5, 65, 78, 95};
    for (auto e: a) {
        bs.set(e);
    }

    for (auto e: a) {
        cout << e << "->" << bs.test(e) << endl;
    }
    cout << "==================" << endl;
    bs.reset(1);
    bs.reset(5);

    for (auto e: a) {
        cout << e << "->" << bs.test(e) << endl;
    }
    // a中没有的值
    cout << "a中没有的值:" << 10 << "->" << bs.test(10) << endl;

}

1.3、位图的模拟实现

这里我们用的int作为一个区间大小（32），所以是mod 32。如果是char就mod 8。

#include <vector>

// 位图
// 给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。【腾讯】
namespace xp {
    template<size_t N>
    class bitset {
    public:
        bitset() {
            _bs.resize(N / 32 + 1, 0); // 当N很大时，位图的长度范围是1～2^32
        }

        void set(size_t x) {
            assert(x <= N);
            size_t i = x / 32; // 找到第几个int（32位）
            size_t j = x % 32;

            _bs[i] |= (1 << j);// 将该位置置1
        }

        void reset(size_t x) {
            assert(x <= N);
            size_t i = x / 32; // 找到第几个int（32位）
            size_t j = x % 32;

            _bs[i] &= ~(1 << j);// 将该位置置0
        }

        bool test(size_t x) {
            assert(x <= N);
            size_t i = x / 32; // 找到第几个int（32位）
            size_t j = x % 32;

            if (_bs[i] & (1 << j))
                return true;// 这个值存在
            else
                return false;// 这个值不存在
        }

    private:
        vector<int> _bs;
    };

1.4、位图相关面试题

  1. 给40亿个不重复的无符号整数，没排过序。给一个无符号整数，如何快速判断一个数是否在这40亿个数中。【腾讯】

    答：使用位图，位图的大小取决于无符号整数的区间，无符号整数的范围是0～2^32-1即0～4294967295（大约43亿）。在32位平台下就可以将这40亿个整数映射到位图中。映射完后，判断一个数是否在这40亿个数中只需要调用test函数判断该数映射的bit位是否为1，为1就在，为0就不在。

  2. 给两个文件，分别有100亿个整数，我们只有1G内存，如何找到两个文件交集。

    答：使用两个位图，位图1存其中的100亿整数，位图2存其中的另100亿整数，其中位图占用的内存大小 = 2^32bit = 512MB，两个位图就是1GB。之后再一一对比两个位图中相同位置的bit位上都为1的整数就是交集。

  3. 位图应用变形：1个文件有100亿个int，1G内存，设计算法找到出现次数不超过2次的所有整数。

    答：有两个方案：

    方案一：使用一个位图，让每两个比特位映射一个整数，这样就需要2^33个比特位（必须在64位平台下），也就是1GB的内存。两个比特位表示为：00，01，10，11。当一个整数第一次映射的时候，位图的映射位置的这两个比特位中第二个比特位设置为1，第二次映射的时候，位图的映射位置的这两个比特位中第一个比特位设置为1，第二个比特位设置为0。以此类推。其中不超过两次的整数就是映射后比特位为00和01的。

    方案二：使用两个位图，一个整数映射到两个位图的同一个位置，一个位图的这个位置的比特位作为第一个比特位，一个位图的这个位置的比特位作为第二个比特位，其实和方案一差不多，就是两个比特位记录出现的次数。这里两个位图占用的内存大小就是2*512MB=1GB。当一个整数第一次映射的时候，第二个位图的映射位置的比特位设置为1，第二次映射的时候，第一个位图的映射位置的比特位设置为1，第二个位图的映射位置的比特位设置为0。以此类推。其中不超过两次的整数就是映射后比特位为00和01的。

这里仅贴使用两个位图的代码：

template<size_t N>
    class two_bitset {
    public:
        void set(size_t x) {
            if (_bs1.test(x) == false && _bs2.test(x) == false) {
                // 00 -> 01
                _bs2.set(x);
            } else if (_bs1.test(x) == false && _bs2.test(x) == true) {
                // 01 -> 10
                _bs1.set(x);
                _bs2.reset(x);
            } else {

                _bs1.set(x);
                _bs2.set(x);
            }
        }

        size_t test(size_t x) {
            if (_bs1.test(x) == false && _bs2.test(x) == false) {
                return 0;
            } else if (_bs1.test(x) == false && _bs2.test(x) == true) {
                // 01 -> 10
                return 1;
            } else {
                return 2;// 大于等于2次
            }
        }

    private:
        bitset<N> _bs1;
        bitset<N> _bs2;
    };

2、布隆过滤器（Bloom Filter）

2.1、布隆过滤器的概念

布隆过滤器是一种空间效率很高的概率型数据结构，用于判断一个元素是否属于一个集合。它通过一系列哈希函数将元素映射到一个位数组中（即将一个元素映射到多个位置），并根据位数组中的值来判断元素是否存在。

特点：布隆过滤器可以用来快速判断一个元素不在集合中，但是无法确定一个元素是否一定在集合中。它的查询操作是常数时间复杂度，但存在一定的误判率。

应用场景：

  • 在缓存系统中判断一个数据是否存在于缓存中，从而减少缓存不命中率。
  • 在网络爬虫中过滤已经访问过的 URL，避免重复访问。
  • 在分布式系统中进行快速的数据定位。

优点：空间效率高，比哈希表占用更少的内存。查询效率高，时间复杂度低。

缺点：存在一定的误判率，即可能将不在集合中的元素误认为在集合中。不能删除元素，除非重新构建布隆过滤器。

2.2、布隆过滤器的插入

布隆过滤器的的映射规则：将一个元素映射到多个位置。下面我们模拟实现的时候，使用三个哈希函数来映射三个位置。

布隆过滤器也是使用位图来实现的，只不过它的位图的长度要更长，以防止映射位置太少而导致误判率太高。

而哈希函数个数和布隆过滤器长度的选择是有个最佳比例的（有大佬证明了）布隆过滤器

这个比例就是

其中

我们假设k为3，m/n就约等于4.34。

哈希函数：这里默认的插入对象是string，如果插入的数据是自定义类型，可以自己写仿函数传入。

struct HashFuncBKDR {
    size_t operator()(const string &str) {
        unsigned int seed = 131; // 31 131 1313 13131 131313 etc..
        unsigned int hash = 0;

        for (auto &e: str) {
            hash = hash * seed + e;
        }
        return hash;
    }
};

struct HashFuncAP {
    size_t operator()(const string &str) {
        unsigned int hash = 0;
        int i;
        for (i = 0; i < str.size(); i++) {
            if ((i & 1) == 0) {
                hash ^= ((hash << 7) ^ (str[i]) ^ (hash >> 3));
            } else {
                hash ^= (~((hash << 11) ^ (str[i]) ^ (hash >> 5)));
            }
        }
        return hash;
    }

};

struct HashFuncDJB {
    size_t operator()(const string &str) {
        unsigned int hash = 5381;

        for (auto &e: str) {
            hash += (hash << 5) + e;
        }
        return hash;
    }

};

插入代码：

namespace xp {
    template<size_t N>
    class bitset {
    public:
        bitset() {
            _bs.resize(N / 32 + 1, 0); // 当N很大时，位图的长度范围是1～2^32
        }

        void set(size_t x) {
            assert(x <= N);
            size_t i = x / 32; // 找到第几个int（32位）
            size_t j = x % 32;

            _bs[i] |= (1 << j);// 将该位置置1
        }

        void reset(size_t x) {
            assert(x <= N);
            size_t i = x / 32; // 找到第几个int（32位）
            size_t j = x % 32;

            _bs[i] &= ~(1 << j);// 将该位置置0
        }

        bool test(size_t x) {
            assert(x <= N);
            size_t i = x / 32; // 找到第几个int（32位）
            size_t j = x % 32;

            if (_bs[i] & (1 << j))
                return true;// 这个值存在
            else
                return false;// 这个值不存在
        }

    private:
        vector<int> _bs;
    };
}

struct HashFuncBKDR {
    size_t operator()(const string &str) {
        unsigned int seed = 131; // 31 131 1313 13131 131313 etc..
        unsigned int hash = 0;

        for (auto &e: str) {
            hash = hash * seed + e;
        }
        return hash;
    }
};

struct HashFuncAP {
    size_t operator()(const string &str) {
        unsigned int hash = 0;
        int i;
        for (i = 0; i < str.size(); i++) {
            if ((i & 1) == 0) {
                hash ^= ((hash << 7) ^ (str[i]) ^ (hash >> 3));
            } else {
                hash ^= (~((hash << 11) ^ (str[i]) ^ (hash >> 5)));
            }
        }
        return hash;
    }

};

struct HashFuncDJB {
    size_t operator()(const string &str) {
        unsigned int hash = 5381;

        for (auto &e: str) {
            hash += (hash << 5) + e;
        }
        return hash;
    }

};

template<size_t N,
        class K=string,
        class Hash1 = HashFuncBKDR,
        class Hash2 = HashFuncAP,
        class Hash3 = HashFuncDJB
>
class BloomFilter {
public:
    void set(const K &s) {
        int hash1 = Hash1()(s) % M;
        int hash2 = Hash2()(s) % M;
        int hash3 = Hash3()(s) % M;

        // 映射三个位置
        _bs.set(hash1);
        _bs.set(hash2);
        _bs.set(hash3);

    }


private:
    static const size_t M = 8*N;
    xp::bitset<M> _bs;
};

2.3、布隆过滤器的模拟实现

判断一个元素在不在这个位图中，可以看其映射的位置是否存在比特位为0的，为0一定不存在。其中一个位为1不一定存在，全部位（这里是3个位）位1才存在（也可能误判）。

因此整体代码为:

namespace xp {
    template<size_t N>
    class bitset {
    public:
        bitset() {
            _bs.resize(N / 32 + 1, 0); // 当N很大时，位图的长度范围是1～2^32
        }

        void set(size_t x) {
            assert(x <= N);
            size_t i = x / 32; // 找到第几个int（32位）
            size_t j = x % 32;

            _bs[i] |= (1 << j);// 将该位置置1
        }

        void reset(size_t x) {
            assert(x <= N);
            size_t i = x / 32; // 找到第几个int（32位）
            size_t j = x % 32;

            _bs[i] &= ~(1 << j);// 将该位置置0
        }

        bool test(size_t x) {
            assert(x <= N);
            size_t i = x / 32; // 找到第几个int（32位）
            size_t j = x % 32;

            if (_bs[i] & (1 << j))
                return true;// 这个值存在
            else
                return false;// 这个值不存在
        }

    private:
        vector<int> _bs;
    };
}

struct HashFuncBKDR {
    size_t operator()(const string &str) {
        unsigned int seed = 131; // 31 131 1313 13131 131313 etc..
        unsigned int hash = 0;

        for (auto &e: str) {
            hash = hash * seed + e;
        }
        return hash;
    }
};

struct HashFuncAP {
    size_t operator()(const string &str) {
        unsigned int hash = 0;
        int i;
        for (i = 0; i < str.size(); i++) {
            if ((i & 1) == 0) {
                hash ^= ((hash << 7) ^ (str[i]) ^ (hash >> 3));
            } else {
                hash ^= (~((hash << 11) ^ (str[i]) ^ (hash >> 5)));
            }
        }
        return hash;
    }

};

struct HashFuncDJB {
    size_t operator()(const string &str) {
        unsigned int hash = 5381;

        for (auto &e: str) {
            hash += (hash << 5) + e;
        }
        return hash;
    }

};

template<size_t N,
        class K=string,
        class Hash1 = HashFuncBKDR,
        class Hash2 = HashFuncAP,
        class Hash3 = HashFuncDJB
>
class BloomFilter {
public:
    void set(const K &s) {
        int hash1 = Hash1()(s) % M;
        int hash2 = Hash2()(s) % M;
        int hash3 = Hash3()(s) % M;

        // 映射三个位置
        _bs.set(hash1);
        _bs.set(hash2);
        _bs.set(hash3);

    }

    bool test(const K &s) {
        int hash1 = Hash1()(s) % M;
        int hash2 = Hash2()(s) % M;
        int hash3 = Hash3()(s) % M;

        if (_bs.test(hash1) == false)
            return false;
        if (_bs.test(hash2) == false)
            return false;
        if (_bs.test(hash3) == false)
            return false;

        return true;// 也可能误判

    }

private:
    static const size_t M = 8*N;
    xp::bitset<M> _bs;
//    std::bitset<M> *_bs = new bitset<M>;// 也可以用库里面的
};

2.4、布隆过滤器相关面试题

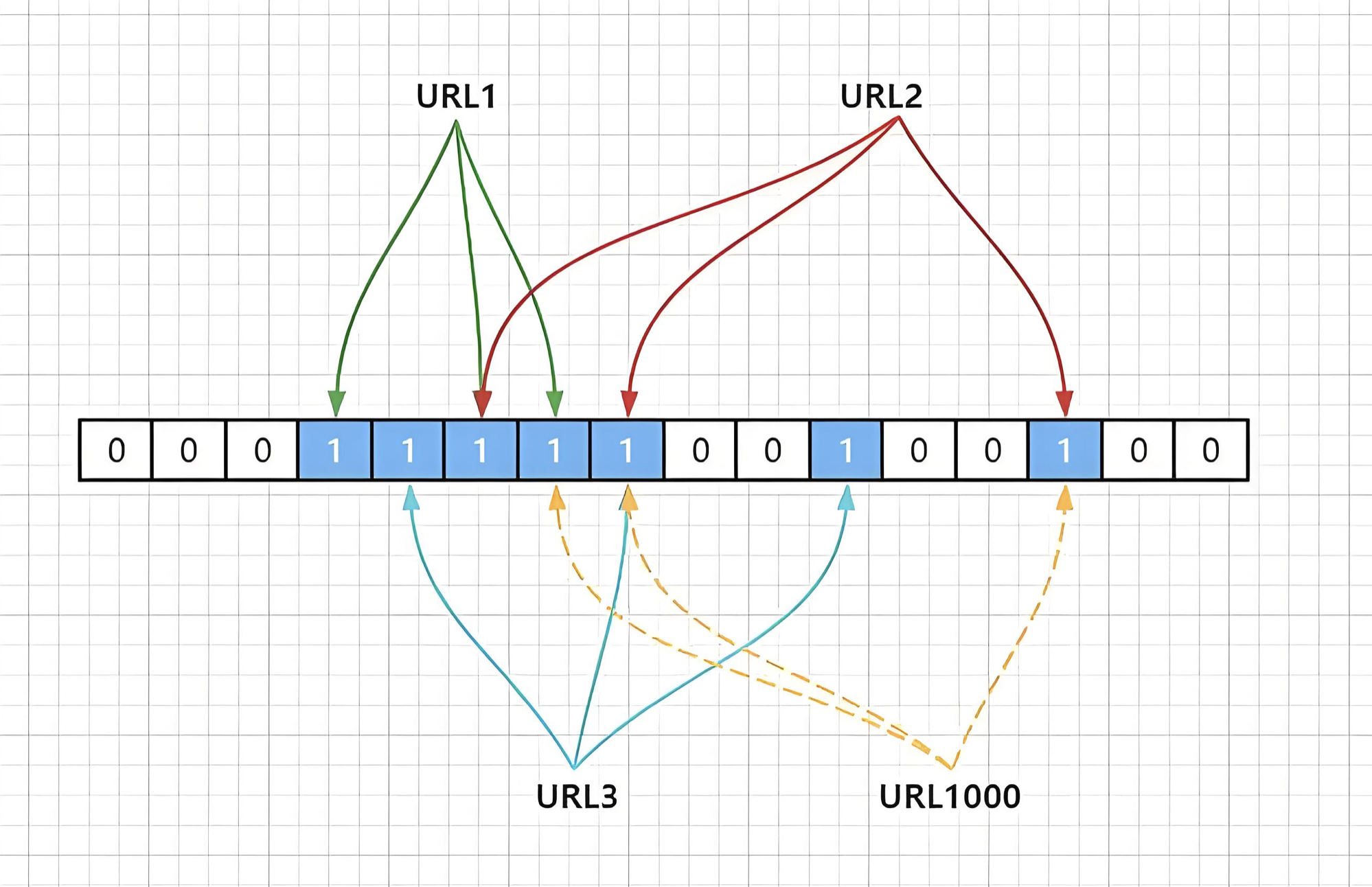
  1. 给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？分别给出精确算法和近似算法。

    答：精确算法使用哈希分割（哈希切分，下面讲）。近似算法使用布隆过滤器。

  2. 如何扩展BloomFilter使得它支持删除元素的操作。

    答：使用多个位图进行对该位进行计数，但是会使得占用的内存变大。

3、哈希切分（哈希切割）

看这个问题：给两个文件，分别有100亿个query，我们只有1G内存，如何找到两个文件交集？给出精确算法。

我们假设一个请求（query）是50字节，那么100亿个请求，就是500亿字节，约等于50GB，一般来说50GB的文件内存是放不下的。

那么怎么处理呢？

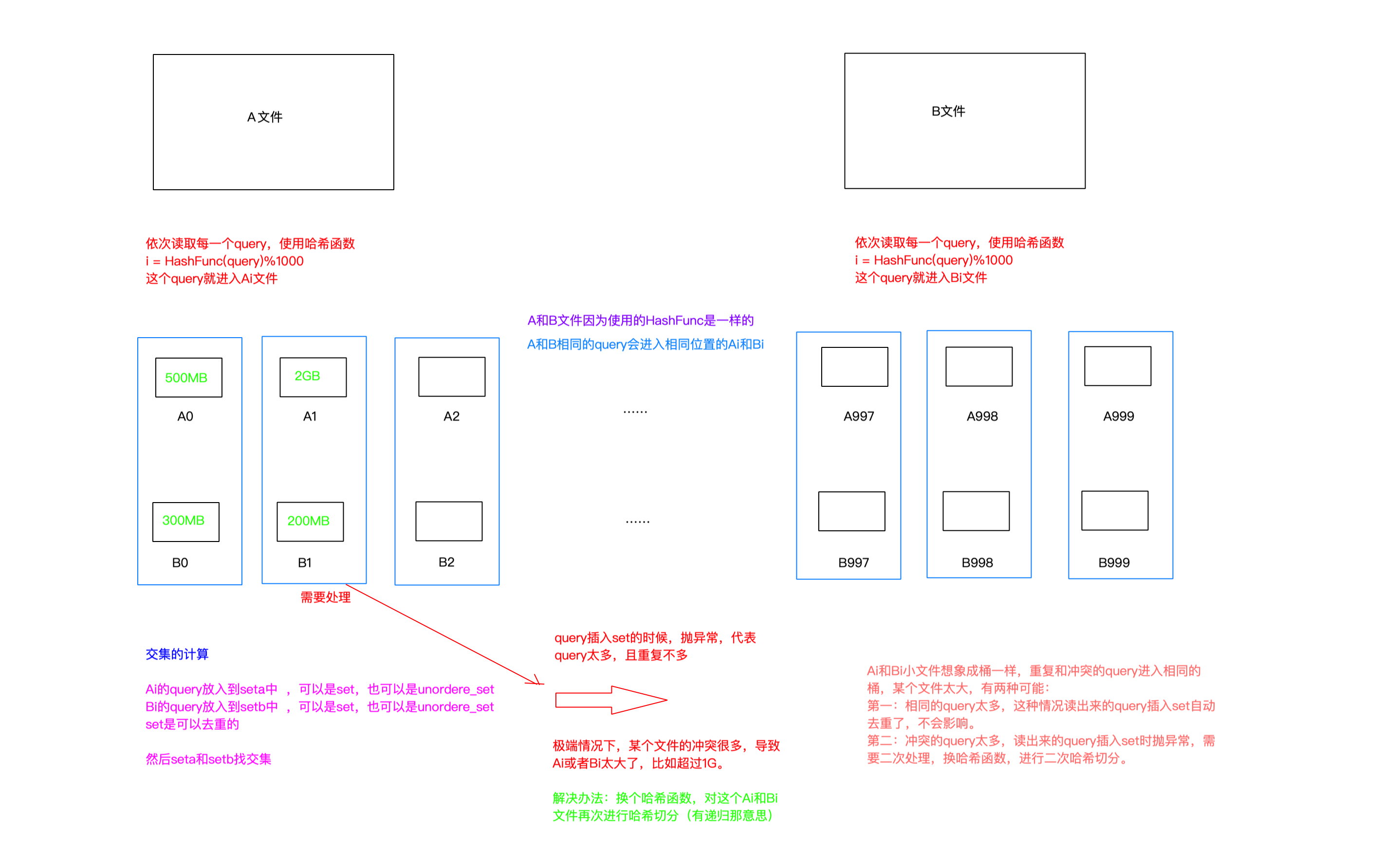
我们可以讲这个50GB的文件使用哈希函数切分为文件大小不同的1000份小文件（初始是没有数据，只是创建了空文件，等待后续哈希函数映射进行插入数据），平均下来每个文件大小就是500MB。为什么是1000份？假设是切分为500小文件，那如果使用哈希函数时，有占用1GB以上的query放到一个小文件中，就会导致放不进内存。这种情况的概率是很大的。切分为1000份，这种情况的概率就会变小，但不保证0概率，就算某个小文件的大小大于1GB，也是可以解决的（再次切分，下面会讲）。

文字解释太生硬，下面直接看图：

问题：给一个超过100G大小的log 文件, log中存着IP地址, 设计算法找到出现次数最多的IP地址？如何找到top K的IP？

答：采用哈希切分，将这个100GB大小的文件切分大小不一为100个小文件（初始是没有数据，只是创建了空文件，等待后续哈希函数映射进行插入数据），对每个小文件使用map<string,int>（这里如果文件太大，map插入IP可能会出现异常，那么就换哈希函数进行二次切分），得到该文件出现次数最多的IP，再对比其他小文件文件的出现次数最多的IP，进行比较，得到整体出现次数最多的IP。找top K的IP只需要创建一个存K个元素的小堆，再依次对比插入。

4、海量数据处理

海量数据问题特征：数据量大，内存存不下

  1. 先考虑具有特点的数据结构能否解决。比如：位图、堆、布隆过滤器等等

  2. 大事化小思路。哈希切分（不能平均切分）切小以后，放到内存中能处理

OKOK，C++ 位图和布隆过滤器就到这里。如果你对Linux和C++也感兴趣的话，可以看看我的主页哦。下面是我的github主页，里面记录了我的学习代码和leetcode的一些题的题解，有兴趣的可以看看。

Xpccccc的github主页

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1583071.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【通信原理笔记】【三】模拟信号调制——3.5 角度调制（FM、PM）与其频谱特性

【通信原理笔记】【三】模拟信号调制——3.5 角度调制（FM、PM）与其频谱特性

文章目录 前言一、相位与频率二、PM和FM的数学表示三、FM的频谱四、FM信号的带宽——卡松公式总结 前言 在之前介绍的几种调制方式中&#xff0c;我提到信噪比时计算的是用户解调后的信噪比&#xff0c;然而在北邮通信原理课中考虑的是解调器输入的信噪比&#xff0c;即考虑的…
阅读更多...
一键破解WB多条带--Swissprot数据库

一键破解WB多条带--Swissprot数据库

WB条带不符合预期&#xff1f; 不要着急扔掉结果&#xff0c;有可能是重要信息忽略了哟&#xff01;Swissprot带你了解蛋白大小的前因后果。 UniProtKB/Swiss-Prot (reviewed) 是一个高质量人工注释且非冗余的蛋白序列数据库。其中包含各类实验结果、计算得到的特征信息和文献…
阅读更多...
损失函数-交叉熵 梯度下降

损失函数-交叉熵 梯度下降

文章目录 1、交叉熵的简单例子1.2、Classification Error&#xff08;分类错误率&#xff09;1.3、Mean Squared Error (均方误差)1.4、交叉熵损失函数1.5、二分类 2、什么是梯度下降法&#xff1f;2.2、梯度下降法的运行过程2.3、二元函数的梯度下降 1、交叉熵的简单例子 参考…
阅读更多...
动力与智能的碰撞：高效控制下的Profinet与EtherCAT逆变器融合

动力与智能的碰撞：高效控制下的Profinet与EtherCAT逆变器融合

在实施工业自动化解决方案时&#xff0c;特别是当涉及到西门子S7-1200/1500系列PLC的集成时&#xff0c;一个常见的问题就是是确保不同通信协议之间的兼容性。在这种情况下&#xff0c;我们面临的是将这些PLC与支持EtherCAT通信功能的逆变器设备相连接的需求。西门子PLC通常利用…
阅读更多...
浏览器密码框明文密文兼容edge的问题

浏览器密码框明文密文兼容edge的问题

在网页中注册会员的时候&#xff0c;经常需要输入用户名&#xff08;账号&#xff09;和密码&#xff0c;在输入密码的时候&#xff0c;为了防止用户输错密码&#xff0c;经常会给密码框加一个小功能&#xff0c;就是点击密码框右侧闭着的小眼睛&#xff0c;可以让密文变成明文…
阅读更多...
蓝桥杯真题 买不到的数目 结论题 数论

蓝桥杯真题 买不到的数目 结论题 数论

&#x1f468;‍&#x1f3eb; 题目地址 &#x1f468;‍&#x1f3eb; 数论&#xff1a;pxpy 不能表示的最大数为pq-p-q的证明 最大能表示的数为&#xff1a; p q − p − q ( p − 1 ) ( q − 1 ) pq-p-q(p-1)(q-1) pq−p−q(p−1)(q−1) 则最大不能表示的数为 ( p − …
阅读更多...
Tubi 十岁啦！

Tubi 十岁啦！

Tubi 今年十岁了&#xff0c;这十年不可思议&#xff0c;充满奇迹&#xff01; 从硅谷一个名不见经传的创业小作坊&#xff0c;转变成为四分之一美国电视家庭提供免费流媒体服务的北美领先的平台&#xff1b; 从费尽心力终于签下第一笔内容合作协议&#xff0c;到现在与 450 …
阅读更多...
实验：基于Red Hat Enterprise Linux系统建立RAID磁盘阵列

实验：基于Red Hat Enterprise Linux系统建立RAID磁盘阵列

目录 一. 实验目的 二. 实验内容 三. 实验设计描述及实验结果 什么是磁盘阵列&#xff08;RAID&#xff09; 1. 为虚拟机添加4块大小为20G的硬盘nvme0n【2-5】&#xff0c;将nvme0n【2、3、4】三块硬盘 建立为raid5并永久挂载&#xff0c;将RAID盘全部空间制作逻辑卷&#…
阅读更多...
软件开发自媒体获客避坑：啥都能干＝啥都抓不着=啥都干不了。

软件开发自媒体获客避坑：啥都能干＝啥都抓不着=啥都干不了。

我就结合我的经验谈一下粗浅的看法&#xff0c;权当抛砖引玉了。 一、自媒体流量本质是一种泛流量 自媒体流量通常指的是通过自媒体平台&#xff08;如微信公众号、微博、知乎等&#xff09;获取的泛流量。泛流量是指广泛的、来自不同渠道的流量&#xff0c;包括通过搜索引擎…
阅读更多...
面试官为什么喜欢考察Vue底层原理

面试官为什么喜欢考察Vue底层原理

&#x1f90d; 前端开发工程师、技术日更博主、已过CET6 &#x1f368; 阿珊和她的猫_CSDN博客专家、23年度博客之星前端领域TOP1 &#x1f560; 牛客高级专题作者、打造专栏《前端面试必备》 、《2024面试高频手撕题》 &#x1f35a; 蓝桥云课签约作者、上架课程《Vue.js 和 E…
阅读更多...
C语言面试题之检查二叉树平衡性

C语言面试题之检查二叉树平衡性

检查二叉树平衡性 实例要求 1、实现一个函数&#xff0c;检查二叉树是否平衡&#xff1b;2、在这个问题中&#xff0c;平衡树的定义如下&#xff1a;任意一个节点&#xff0c;其两棵子树的高度差不超过 1&#xff1b; 示例 1: 给定二叉树 [3,9,20,null,null,15,7]3/ \9 20/…
阅读更多...
OSPF数据报文格式

OSPF数据报文格式

OSPF协议是跨层封装的协议&#xff0c;跨四层封装&#xff0c;直接将应用层的数据封装在网络层协议后面&#xff0c;IP协议包中协议号字段对应的数值为——89 OSPF的头部信息&#xff1a; ——所有数据包公有的信息 版本&#xff1a;OSPF版本 在IPV4中一般使用OSPFV2&#xf…
阅读更多...
【3GPP】【核心网】核心网/蜂窝网络重点知识面试题二（超详细）

【3GPP】【核心网】核心网/蜂窝网络重点知识面试题二（超详细）

1. 欢迎大家订阅和关注&#xff0c;3GPP通信协议精讲&#xff08;2G/3G/4G/5G/IMS&#xff09;知识点&#xff0c;专栏会持续更新中.....敬请期待&#xff01; 目录 1. 对于主要的LTE核心网接口&#xff0c;给出运行在该接口上数据的协议栈&#xff0c;并给出协议特征 2. 通常…
阅读更多...
ShardingSphere-ShardingSphere读写分离和数据脱敏

ShardingSphere-ShardingSphere读写分离和数据脱敏

文章目录 一、读写分离1.1 读写分离1.2 读写分离应用方案1.3 分表+读写分离1.4 分库分表+读写分离二、ShardingSphere-JDBC读写分离2.1 创建SpringBoot并添加依赖2.2 创建实体类2.3 创建mapper2.4 配置读写分离2.5 测试测试插入数据测试读测试事务一致性测试负载均衡一、读写分…
阅读更多...
BP实战之猫狗分类数据集

BP实战之猫狗分类数据集

目录 补充知识 python类里面的魔法方法 transforms.Resize() python里面的OS库 BP实战之猫狗分类数据集 猫狗数据集 注意事项 使用类创建自己的猫狗分类数据集 代码 实例化对象尝试 代码 结果 利用DataLoader加载数据集 BP神经网络的搭建以及对象的使用 运行结果…
阅读更多...
【PyQt5篇】使用QtDesigner添加控件和槽

【PyQt5篇】使用QtDesigner添加控件和槽

文章目录 &#x1f354;使用QtDesigner进行设计&#x1f6f8;在代码中添加信号和槽 &#x1f354;使用QtDesigner进行设计 我们首先使用QtDesigner设计界面 得到代码login.ui <?xml version"1.0" encoding"UTF-8"?> <ui version"4.0&q…
阅读更多...
【Qt】：窗口

【Qt】：窗口

窗口 一.概述二.菜单栏1.一个简单的菜单2.添加快捷键3.嵌套子菜单4.添加下划线5.添加图标 三.工具栏1.创建一个简单的工具栏2.设置工具栏的停靠位置 四.状态栏五.浮动窗口 一.概述 Qt窗口是通过QMainWindow类来实现的。 QMainWindow是一个为用户提供主窗口程序的类&#xff0c…
阅读更多...
经典本地影音播放器纯净无广告版

经典本地影音播放器纯净无广告版

MPC-BE&#xff08;Media Player Classic Black Edition&#xff09;是来自 MPC-HC&#xff08;Media Player Classic Home Cinema&#xff09;的俄罗斯开发者重新编译优化后的一款经免费的经典全能影音播放器&#xff0c;纯净无广告&#xff0c;启动速度快&#xff0c;占用消耗…
阅读更多...
ES7-10:async和await、异步迭代..

ES7-10:async和await、异步迭代..

1-ES7新特性 indexof如果没有就返回-1&#xff0c;有就返回索引 如果仅仅查找数据是否在数组中,建议使用includes,如果是查找数据的索引位置,建议使用indexOf更好一些 2-ES8-async和await 所有的需要异步处理的Promise对象都写在async中await等待结果 async、await 使异步操…
阅读更多...
HEC-HMS水文模型

HEC-HMS水文模型

HEC-HMS是美国陆军工程兵团水文工程中心开发的一款水文模型。HMS能够模拟各种类型的降雨事件对流域水文&#xff0c;河道水动力以及水利设施的影响&#xff0c;在世界范围内得到了广泛的应用。它有着完善的前后处理软件&#xff0c;能有效减轻建模的负担&#xff1b;能够与HEC开…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023