吴恩达机器学习理论基础—决策树模型
决策树模型(Decision Trees)
采用猫狗分类的数据集,同时拥有三个基本的特征(输入)作为模型建立时使用的数据集。
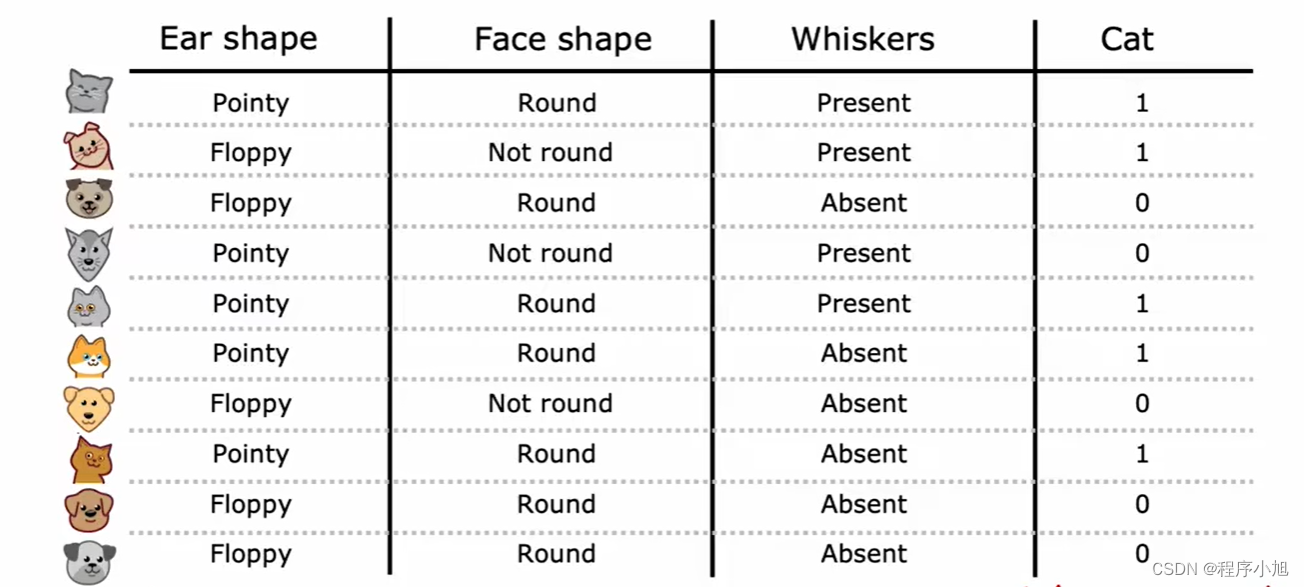
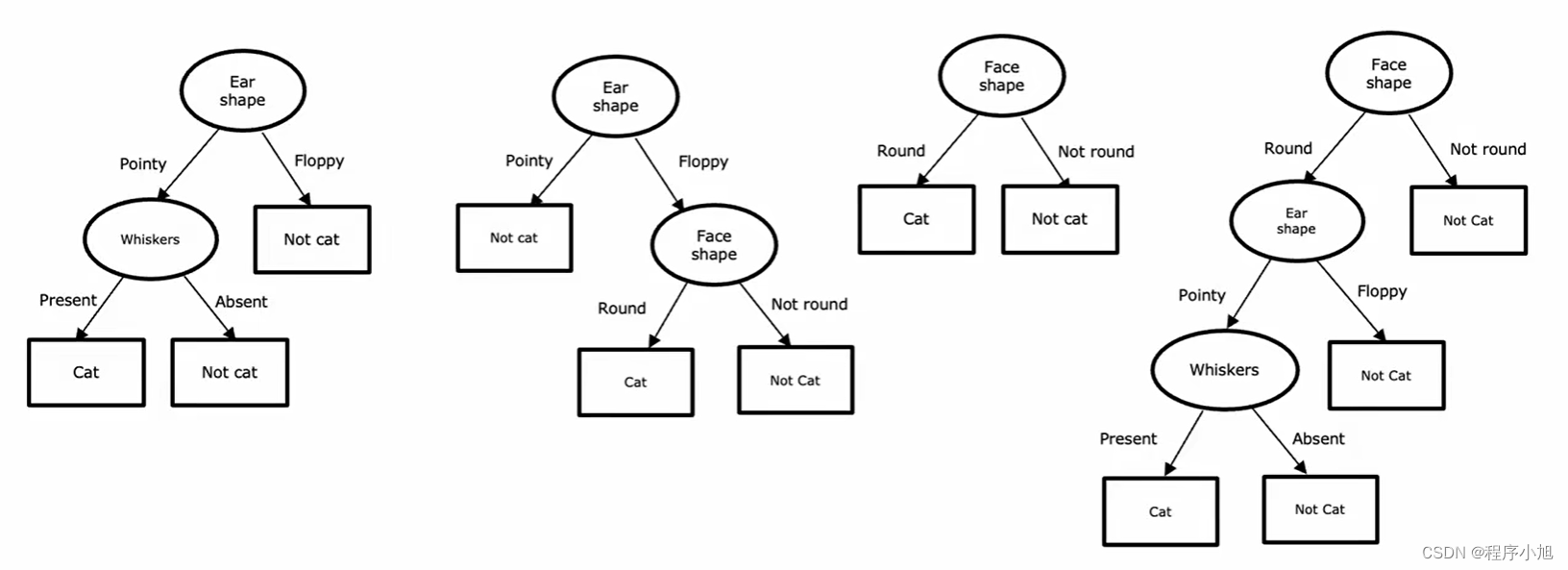
将构造出来的决策树,分为了决策结点和叶子节点(预测节点)根据不同的节点进行预测和选择,从而得到想要的结果。构造的简单决策树如图所示。
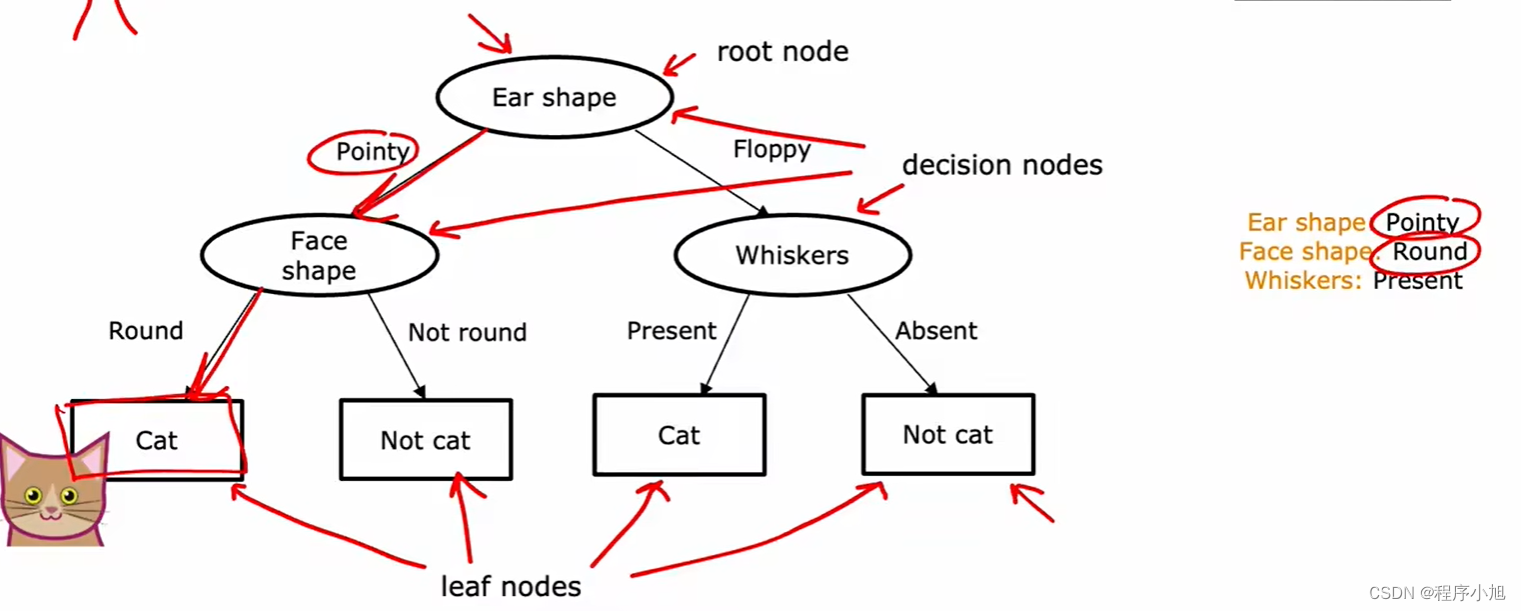
采用不同的决策树构造算法会得到不同的决策树类型。需要通过模型的评估准则来对决策树进行评价。
决策树学习过程
学习过程的第一步,必须决定在根节点使用什么特征。

之后将结点进行进一步的细分完成做分支的建立过程。并产生预测节点的叶节点。之后采用相同的过程构造出右侧的分支结点。

首先决定在每个节点上使用哪些功能进行拆分,通过选择获得Maximize purity(最大纯度)
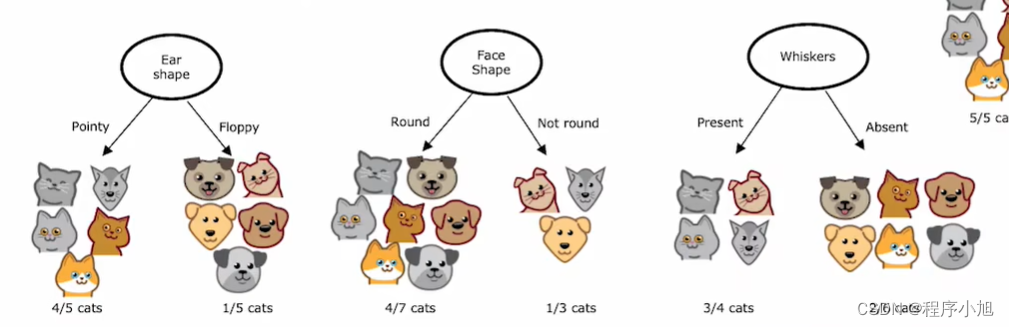
第二个需要解决的问题是,决策在什么时候停止的问题。(个人理解是剪枝的问题,解决模型的过拟合问题)
- 可以得到唯一的预测结果(确定不同的分类)
- When splitting a node will result in the tree exceeding a maximum depth
- 得到的分支结点不值得在进一步进行拆分的情况
测量纯度(Measuring purity)
绘制熵函数(H)通过熵函数来确认,根据不同的比例确定不同的熵的值来进行确定。
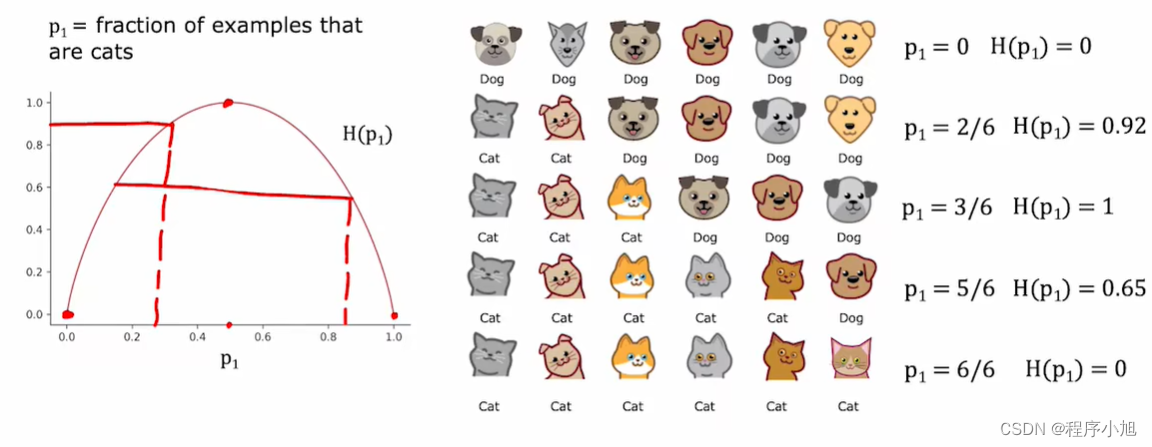
对于决策时中的公式推导基尼系数等一些概念(参考教材西瓜书中的系统介绍)。

信息增益的选择拆分(Choosing a split: Information Gain)
在决策树的学习中,熵的减少称为信息增益。在计算的过程中,使用平均加权来进行实现来提高其对应的纯度信息。(选择其中的熵最低的一项进行实现)

最低加权平均
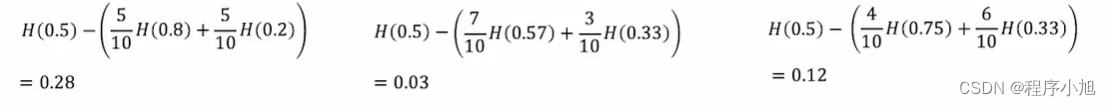
我们使用信息熵来进行特征的选取与划分,从而确定了不同的决策树构造算法。