1. 递归实现的缺陷
在以前的文章中我们把快速排序和归并排序的递归实现方式进行了介绍,但是在校招面试和在企业的日常开发过程中,仅掌握递归方法是不够的,因为递归也有它的缺陷。
我们知道在函数调用过程中会在内存中建立栈帧,栈帧的建立是会消耗空间的。而递归最致命的缺陷就是:在极端情况下,当栈帧的深度太深时,栈空间不够用,就会导致栈溢出!
1.1 栈溢出的例子
可以举一个简单的例子来证明存在栈溢出的情况。
比如:我们用递归实现 1 + 2 + 3 + …… + n 的求和。
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int func(int n)
{
return n == 1 ? 1 : n + func(n - 1);
}
int main()
{
int n = 0;
scanf("%d", &n);
int sum = func(n);
printf("%d\n", sum);
return 0;
}
当输入的 n = 10000 时 ,调试结果如下:

2. 递归改非递归的实现方式
通常来说,递归改非递归有两种方式:
1. 直接改成循环(迭代);
2. 借助数据结构的栈模拟。
3. 快速排序的非递归 — 使用栈
1.首先先来观察快排的递归实现(三种方法均可,这里用的"前后"指针法 ):

通过观察我们发现,每次递归调用传过去的是一个数组和一个区间,数组不用多说,这个区间就是我们的突破点。
也就是说我们要想一个方法来拿到每左右子区间,再对它们分别进行排序,这样才能模拟出递归的过程。那该如何做呢?借助数据结构的栈。
2.非递归的代码实现:
注意:由于C语言没有栈函数的库,所以这里使用的栈要提前准备好,实现栈的过程这里不再介绍。若想了解请前往我的主页。
void Swap(int* p1, int* p2)
{
int tmp = *p1;
*p1 = *p2;
*p2 = tmp;
}
void QuickSortNonR(int* arr, int n)
{
ST st;
StackInit(&st);
//先入右,后入左
StackPush(&st, n - 1);
StackPush(&st, 0);
while (!StackEmpty(&st))
{
//先出左边界
int left = StackTop(&st);
StackPop(&st);
//后出右边界
int right = StackTop(&st);
StackPop(&st);
int keyi = left;
int prev = left;//关键字默认左边第一个元素
int cur = left + 1;
while (cur <= right)
{
//++prev != cur是指当cur和prev重合时不用多于的交换
if (arr[cur] < arr[keyi] && ++prev != cur)
{
Swap(&arr[cur], &arr[prev]);
}
cur++;
}
Swap(&arr[keyi], &arr[prev]);
keyi = prev;
if (keyi + 1 < right)
{
StackPush(&st, right);
StackPush(&st, keyi + 1);
}
if (left < keyi - 1)
{
StackPush(&st, keyi - 1);
StackPush(&st, left);
}
}
StackDestory(&st);
}
排序结果如下:
3.步骤总结:
3.1.首先要先把数组 最右端 和 最左端 入栈,这样就有了一个初始区间,然后开始循环。
3.2.取出栈顶的两个数据,分别赋给 left 和 right,注意在这之后要pop掉取出的数据;
3.3.再使用前后指针法走完一趟后就得到了keyi ;
3.4.然后数组就被 keyIndex 分成了两个子区间,分别是:
左区间:[left,keyi -1]
右区间:[keyi +1,right]
3.5.由于我们一般是先排左区间,再排右区间,根据栈的后进先出特性,所以要先入右区间。
分别将左区间和右区间入栈,注意这里要判断:
keyi + 1 < right
left < keyi - 1
否则会出现数组访问越界或是死循环的情况。
3.6.循环结束后,销毁栈。
4.总结一下
最后我们要知道的是,快排的非递归并不会使性能受到破坏,它的时间复杂度也是O(N*logN),它的效率依旧极高。使用非递归的主要原因就是防止溢出。
4. 归并排序的非递归 — 使用循环
首先我们知道归并排序的思想是将两组有序的数据合成一组有序的数据。
1. 循环步骤如下:
1.1 那么我们会这样想,当第一组只有1个数据,第二组也只有1个数据时,我们认为这两个数是有序的,把它们一一归并到一个临时数组中,此时临时数组里的2个数据就有序了。
1.2.当第一组有2个有序数据,第二组也有2个有序数据时,把它们两两归并到一个临时数组中此时临时数组里的4个数据就有序了。
1.3.当第一组有3个有序数据,第二组也有3个有序数据时,把它们三三归并到一个临时数组中,此时临时数组里的6个数据就有序了。
1.4 重复上述步骤……直到全部数据有序为止。
2.循环图解如下:
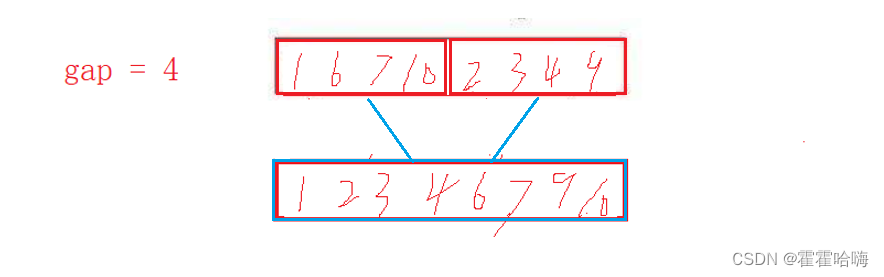
我们假设 gap 为每一组的数据个数,这里最难的是如何控制每一组的范围,即那个区间的边界。
假设循环的初始值从 i = 0 开始,则两组的范围可以分别表示为:
第一组:[ i , i + gap - 1 ]
第二组:[ i + gap , i + 2gap - 1 ]
每组1个数据,一一归,归完后临时数组里的2个数据就有序了;

每组2个数据,二二归,归完后临时数组里的4个数据就有序了;

每组4个数据,四四归,归完后临时数组里的8个数据就有序了;
2. 非递归的代码实现:
这里有两种边界修正问题需要特别注意:
(1)在归并过程中右半区间可能不存在
这时直接跳出循环,把剩下的那一个数据直接拷贝进数组即可。
比如在一一归并时:
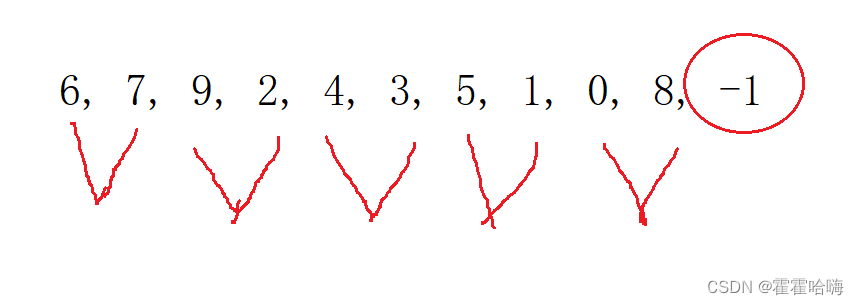
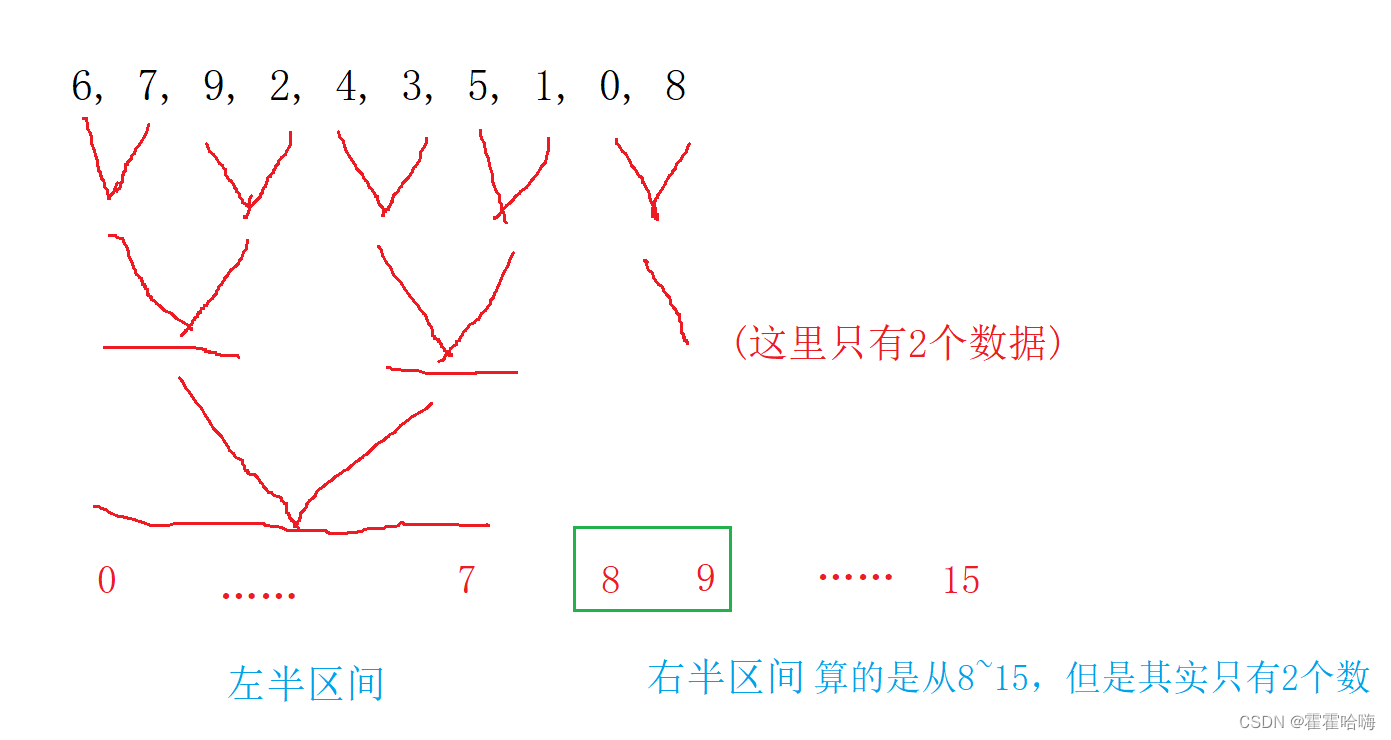
(2)在归并过程中右半区间可能算多了
此时要把右半区间的右边界修改为数组最后一个元素的下标。
//归并排序的非递归
void MergeSortNonR(int* a, int sz)
{
int* tmp = (int*)malloc(sizeof(int) *sz);
int gap = 1; // 每组数据个数
while (gap < sz)
{
for (int i = 0; i < sz; i += 2 * gap)
{
// [i, i+gap-1] [i+gap,i+2*gap-1]
int begin1 = i, end1 = i + gap - 1;
int begin2 = i + gap, end2 = i + 2 * gap - 1;
// 归并过程中右半区间可能就不存在
if (begin2 >= sz)
break;
// 归并过程中右半区间算多了, 修正一下
if (end2 >= sz)
{
end2 = sz - 1;
}
//归并的过程
int index = i;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[index++] = a[begin1++];
}
else
{
tmp[index++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[index++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[index++] = a[begin2++];
}
// 归一部分,拷一部分,没归的就不拷
for (int j = i; j <= end2; ++j)
{
a[j] = tmp[j];
}
}
gap *= 2;
}
free(tmp);
}
排序结果如下:
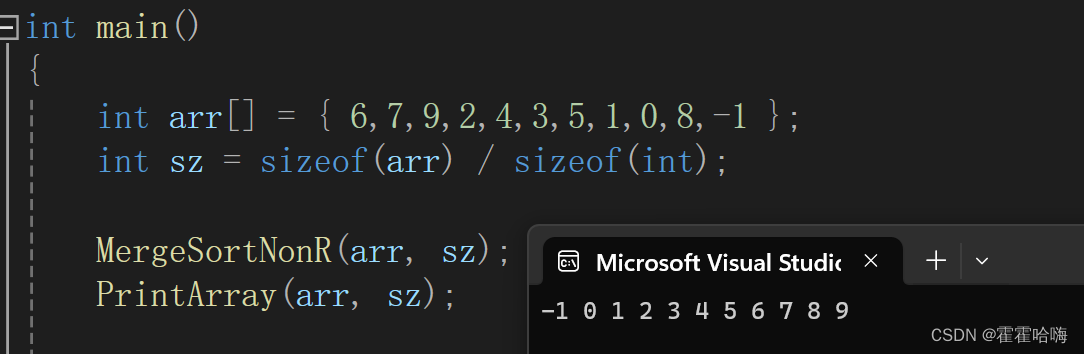
3.总结一下
归并排序的非递归的时间复杂度也是O(N*logN),它与递归的性能也差不多。