目录

130. 被围绕的区域

417. 太平洋大西洋水流问题

结尾

---

130. 被围绕的区域

给你一个 m x n 的矩阵 board ，由若干字符 'X' 和 'O' ，找到所有被 'X' 围绕的区域，并将这些区域里所有的 'O' 用 'X' 填充。

示例 1：

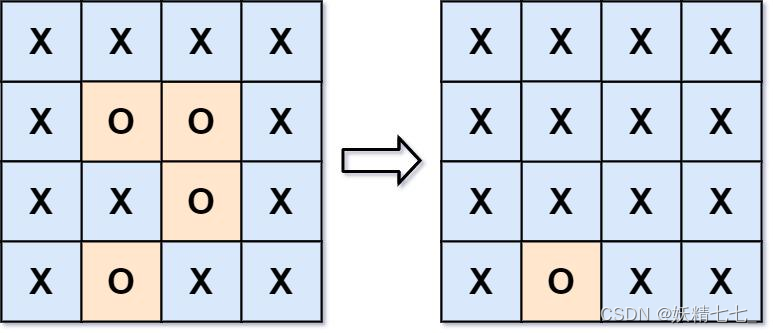
输入：board = [["X","X","X","X"],["X","O","O","X"],["X","X","O","X"],["X","O","X","X"]] 输出：[["X","X","X","X"],["X","X","X","X"],["X","X","X","X"],["X","O","X","X"]] 解释：被围绕的区间不会存在于边界上，换句话说，任何边界上的 'O' 都不会被填充为 'X'。 任何不在边界上，或不与边界上的 'O' 相连的 'O' 最终都会被填充为 'X'。如果两个元素在水平或垂直方向相邻，则称它们是“相连”的。

示例 2：

输入：board = [["X"]] 输出：[["X"]]

提示：

• m == board.length

• n == board[i].length

• 1 <= m, n <= 200

• board[i][j] 为 'X' 或 'O'

问题的关键在于划分集合，一个集合是与边界相连的O区域，另一个集合是不与边界相连的O区域。

因此可以考虑所有与边界相连的O区域进行集合划分。

利用visit进行集合划分。

class Solution {
public:
    vector<vector<bool>> visit;
    int row, col;
    void solve(vector<vector<char>>& board) {
        row = board.size(), col = board[0].size();
        visit = vector<vector<bool>>(row, vector<bool>(col));

        for (int i = 0; i < row; i++) {
            if (board[i][0] == 'O')
                dfs(board, i, 0);
            if (board[i][col - 1] == 'O')
                dfs(board, i, col - 1);
        }
        for (int j = 0; j < col; j++) {
            if (board[0][j] == 'O')
                dfs(board, 0, j);
            if (board[row - 1][j] == 'O')
                dfs(board, row - 1, j);
        }

        for (int i = 0; i < row; i++)
            for (int j = 0; j < col; j++) {
                if (!visit[i][j] && board[i][j] == 'O') {
                    board[i][j] = 'X';
                }
            }
    }
    int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};
    void dfs(vector<vector<char>>& board, int i, int j) {
        // visit
        // 当前
        visit[i][j] = true;
        // 下一层
        for (int k = 0; k < 4; k++) {
            int x = i + dx[k], y = j + dy[k];
            if (x >= 0 && x < row && y >= 0 && y < col && !visit[x][y] &&
                board[x][y] == 'O')
                dfs(board, x, y);
        }
    }
};

在一个二维的棋盘上，棋盘的每个位置要么是 'X' 要么是 'O'。规则是，只有在边缘上或者与边缘上的 'O' 直接或间接相连的 'O' 才不会被 'X' 替换。这个算法的目的是将所有不满足上述条件的 'O' 替换成 'X'。

class Solution {

public:

vector<vector<bool>> visit; // 用于记录棋盘上每个位置是否被访问过

int row, col; // 分别存储棋盘的行数和列数 // 主函数，用于处理棋盘

void solve(vector<vector<char>>& board) {

row = board.size(), col = board[0].size(); // 初始化行和列的大小

visit = vector<vector<bool>>(row, vector<bool>(col)); // 初始化访问标记数组

// 遍历棋盘的四个边缘，对于边缘上的每个 'O'，执行深度优先搜索

for (int i = 0; i < row; i++) {

if (board[i][0] == 'O')

dfs(board, i, 0);

if (board[i][col - 1] == 'O')

dfs(board, i, col - 1);

}

for (int j = 0; j < col; j++) {

if (board[0][j] == 'O')

dfs(board, 0, j);

if (board[row - 1][j] == 'O')

dfs(board, row - 1, j);

} // 遍历整个棋盘，将所有未被访问过的 'O' 替换为 'X'

for (int i = 0; i < row; i++)

for (int j = 0; j < col; j++) {

if (!visit[i][j] && board[i][j] == 'O') {

board[i][j] = 'X';

}

}

} int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1}; // 方向数组，用于表示上下左右四个方向

// 深度优先搜索函数

void dfs(vector<vector<char>>& board, int i, int j) {

visit[i][j] = true; // 标记当前位置已访问

// 遍历当前位置的四个方向

for (int k = 0; k < 4; k++) {

int x = i + dx[k], y = j + dy[k];

// 如果下一个位置在棋盘内，未被访问过，且为 'O'，则对其进行深度优先搜索

if (x >= 0 && x < row && y >= 0 && y < col && !visit[x][y] &&

board[x][y] == 'O')

dfs(board, x, y);

}

}

};

这段代码的关键在于，通过从边缘的 'O' 开始的深度优先搜索（DFS），我们可以找到所有与边缘上的 'O' 直接或间接相连的 'O'，并通过访问数组标记它们。之后，遍历整个棋盘，将所有未被标记为已访问的 'O' 替换为 'X'，从而达到题目的要求。

417. 太平洋大西洋水流问题

有一个 m × n 的矩形岛屿，与 太平洋 和 大西洋 相邻。 “太平洋” 处于大陆的左边界和上边界，而 “大西洋” 处于大陆的右边界和下边界。

这个岛被分割成一个由若干方形单元格组成的网格。给定一个 m x n 的整数矩阵 heights ， heights[r][c] 表示坐标 (r, c) 上单元格 高于海平面的高度 。

岛上雨水较多，如果相邻单元格的高度 小于或等于 当前单元格的高度，雨水可以直接向北、南、东、西流向相邻单元格。水可以从海洋附近的任何单元格流入海洋。

返回网格坐标 result 的 2D 列表 ，其中 result[i] = [r(i), c(i)] 表示雨水从单元格 (ri, ci) 流动 既可流向太平洋也可流向大西洋 。

示例 1：

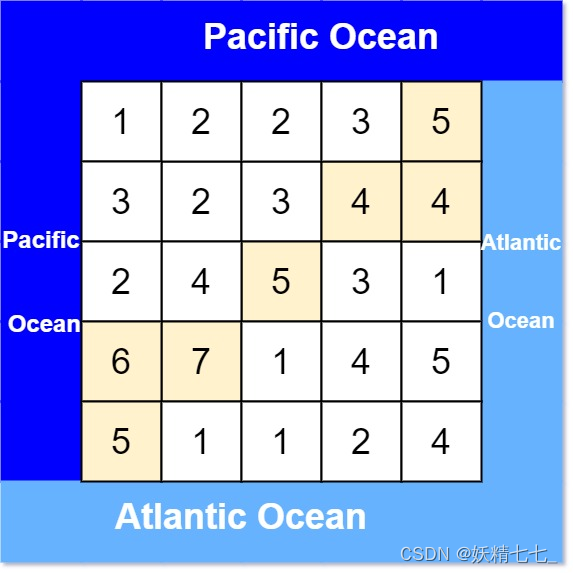
输入: heights = [[1,2,2,3,5],[3,2,3,4,4],[2,4,5,3,1],[6,7,1,4,5],[5,1,1,2,4]] 输出: [[0,4],[1,3],[1,4],[2,2],[3,0],[3,1],[4,0]]

示例 2：

输入: heights = [[2,1],[1,2]] 输出: [[0,0],[0,1],[1,0],[1,1]]

提示：

• m == heights.length

• n == heights[r].length

• 1 <= m, n <= 200

• 0 <= heights[r][c] <= 10(5)

class Solution {
public:
    int row, col;
    vector<vector<int>> pacificAtlantic(vector<vector<int>>& h) {
        row = h.size(), col = h[0].size();

        vector<vector<bool>> visit_pac(row, vector<bool>(col)),
            visit_atl(row, vector<bool>(col));

        for (int i = 0; i < row; i++) {
            dfs(h, i, 0, visit_pac);
            dfs(h, i, col - 1, visit_atl);
        }
        for (int j = 0; j < col; j++) {
            dfs(h, 0, j, visit_pac);
            dfs(h, row - 1, j, visit_atl);
        }

        vector<vector<int>> ret;

        for (int i = 0; i < row; i++) {
            for (int j = 0; j < col; j++) {
                if (visit_atl[i][j] && visit_pac[i][j]) {
                    ret.push_back({i, j});
                }
            }
        }

        return ret;
    }

    int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1};
    void dfs(const vector<vector<int>>& h, int i, int j,
             vector<vector<bool>>& visit) {
        // visit
        // 当前
        visit[i][j] = true;
        // 下一层
        for (int k = 0; k < 4; k++) {
            int x = i + dx[k], y = j + dy[k];
            if (x >= 0 && x < row && y >= 0 && y < col && !visit[x][y] &&
                h[x][y] >= h[i][j]) {
                dfs(h, x, y, visit);
            }
        }
    }
};

这段代码解决的是“太平洋大西洋水流问题”。这个问题要求找出所有同时能流向太平洋和大西洋的单元格。太平洋位于矩阵的左边界和上边界，大西洋位于矩阵的右边界和下边界。水流只能从高到低或在相同高度上流动。给定的矩阵 h 中，每个单元格的值代表该地的高度。

int row, col; // 存储矩阵的行数和列数 // 主函数，返回能流向两大洋的所有单元格

vector<vector<int>> pacificAtlantic(vector<vector<int>>& h) {

row = h.size(), col = h[0].size(); // 初始化行数和列数 // 为太平洋和大西洋分别创建访问矩阵，用于标记是否可达

vector<vector<bool>> visit_pac(row, vector<bool>(col)),

visit_atl(row, vector<bool>(col)); // 从每个大洋的边缘开始，利用DFS标记可达的单元格

for (int i = 0; i < row; i++) {

dfs(h, i, 0, visit_pac); // 从太平洋左边缘开始

dfs(h, i, col - 1, visit_atl); // 从大西洋右边缘开始

}

for (int j = 0; j < col; j++) {

dfs(h, 0, j, visit_pac); // 从太平洋上边缘开始

dfs(h, row - 1, j, visit_atl); // 从大西洋下边缘开始

} vector<vector<int>> ret; // 用于存储结果的矩阵

// 遍历矩阵，找出同时被两个大洋访问过的单元格

for (int i = 0; i < row; i++) {

for (int j = 0; j < col; j++) {

if (visit_atl[i][j] && visit_pac[i][j]) {

ret.push_back({i, j}); // 同时可达两大洋的单元格

}

}

}

return ret; // 返回结果

}

int dx[4] = {1, -1, 0, 0}, dy[4] = {0, 0, 1, -1}; // 方向数组，用于在DFS中向四个方向探索 // DFS函数，用于从特定单元格开始，探索所有可达的单元格

void dfs(const vector<vector<int>>& h, int i, int j,

vector<vector<bool>>& visit) {

visit[i][j] = true; // 标记当前单元格为已访问

// 遍历四个方向

for (int k = 0; k < 4; k++) {

int x = i + dx[k], y = j + dy[k];

// 检查下一个单元格是否在矩阵内，未被访问，且高度不低于当前单元格

if (x >= 0 && x < row && y >= 0 && y < col && !visit[x][y] &&

h[x][y] >= h[i][j]) {

dfs(h, x, y, visit); // 对满足条件的单元格进行DFS

}

}

}

};

代码的核心思想是从两个大洋的边缘开始，反向查找可以流入大洋的单元格。通过DFS，我们可以找到所有从边缘到达当前单元格的路径，并将路径上的单元格标记为可达。最后，检查哪些单元格被两个大洋的访问数组同时标记为可达，这些单元格就是最终的答案，表示这些位置的水既可以流向太平洋，也可以流向大西洋。

初始化行列值和访问数组：通过 h.size() 和 h[0].size() 获取矩阵的行数和列数，并为太平洋与大西洋分别创建一个访问数组（visit_pac 和 visit_atl），用布尔值表示每个单元格是否可以从对应的大洋流入。

从每个大洋的边缘开始深度优先搜索：对于矩阵的四个边缘（上边缘和左边缘为太平洋的边缘，下边缘和右边缘为大西洋的边缘），使用深度优先搜索标记所有从这些边缘可达的单元格。对于太平洋，从左边缘和上边缘的每个单元格开始搜索；对于大西洋，从右边缘和下边缘的每个单元格开始搜索。

合并结果：遍历整个矩阵，检查每个单元格是否同时在 visit_pac 和 visit_atl 中被标记为 true，如果是，表示这个位置的水既可以流向太平洋也可以流向大西洋，将其加入到结果列表中。

返回结果：将所有满足条件的单元格的坐标（行号和列号）作为结果返回。

代码中的 dfs 函数是解决问题的关键，它遵循以下规则：

从当前单元格出发，尝试向四个方向（上、下、左、右）移动。

移动的条件是目标单元格在矩阵内，未被当前大洋的访问数组访问过，且其高度不小于当前单元格的高度（表示水可以从当前单元格流向目标单元格）。

递归地对满足条件的目标单元格执行深度优先搜索，直到不再有满足条件的单元格为止。

结尾

最后，感谢您阅读我的文章，希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点，请随时在评论区留言。

同时，不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中，我将继续探讨这个话题的不同方面，为您呈现更多深度和见解。

谢谢您的支持，期待与您在下一篇文章中再次相遇！