每日一题，今天又刷到一道使用并查集来解决的问题，再次加深了一遍自己对并查集的印象和使用。

题目要求

树可以看成是一个连通且 无环 的 无向 图。

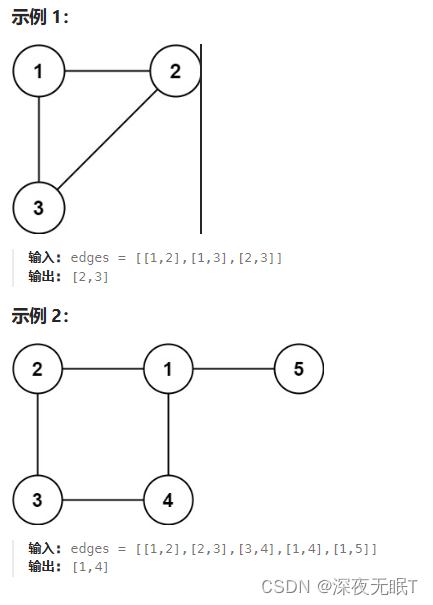
给定往一棵 n 个节点 (节点值 1～n) 的树中添加一条边后的图。添加的边的两个顶点包含在 1 到 n 中间，且这条附加的边不属于树中已存在的边。图的信息记录于长度为 n 的二维数组 edges ，edges[i] = [ai, bi] 表示图中在 ai 和 bi 之间存在一条边。

请找出一条可以删去的边，删除后可使得剩余部分是一个有着 n 个节点的树。如果有多个答案，则返回数组 edges 中最后出现的边。

题目解析及代码

本题明显可以使用并查集的思想，如果判断是否已经来连接可以在两个节点合并前加上一个判断，如果通过find方法发现这两个节点处在一个集体中，那么让记录下这个数据，最后遍历到最后，即使有多个结果是冗余这样也会直接指向最后一个结果。

如果对并查集的思想不是很理解，可以查看我的另外一篇博客，里面做出了详细的解释。

LeetCode547——省份数量（并查集）

下面为实现代码：

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int[] res = new int[2]; 
        int len = edges.length;
        int[] p = new int[len];
        for(int i =0;i<len;i++){
            p[i] = i;
        }
        for(int i =0;i<len;i++){
            int x1 = edges[i][0]-1;
            int x2 = edges[i][1]-1;
            if(find(p,x1)==find(p,x2)){
                res = edges[i];
            }
            union(p,x1,x2);
        }
        return res;
    }
    public void union(int[] p,int index1,int index2){
        int x1 = find(p,index1);
        int x2 = find(p,index2);
        p[x2] = x1; 
    }
    public int find(int[] p,int index){
        if(p[index]!=index){
            p[index] = find(p,p[index]);
        }
        return p[index];
    }
}